A* 演算法

封面圖片由 ChatGPT 生成。
前言
A* 演算法(A* Algorithm),又稱作 A* 搜尋演算法(A* Search Algorithm),是眾多遊戲與人工智慧應用中常見的路徑規劃演算法之一。其演算法結合戴克斯特拉演算法的全局最短路徑特性與貪婪演算法的啟發式搜尋策略,使 A* 演算法兼具效率與準確性,因此廣受歡迎。同時, A* 演算法也廣泛用於機器人導航、地圖路徑規劃等等眾多領域中。

運作原理
A* 演算法的評估函式可以表示如下: $$ f(n) = g(n) + h(n), $$
其中, $n$ 代表目前地點, $g(n)$ 表示從起點到目前地點的實際距離, $h(n)$ 代表目前地點到終點的預估距離。
由以上評估函式,我們可以發現:
- 當設定 $g(n) = 0$ 時, A* 演算法將退化為 $f(n) = h(n)$ ,即僅用到終點的距離作為評估條件,是貪婪演算法。
- 當設定 $h(n) = 0$ 時, A* 演算法將退化為 $f(n) = g(n)$ ,即僅用最短路徑作為評估條件,是戴克斯特拉演算法。
- 如果 $h(n)$ 小於 $n$ 到終點的實際距離時,雖然一定可以求出最佳解,但是需要計算的節點越多,演算法效率越低。
- 如果 $h(n)$ 等於 $n$ 到終點的實際距離時,能尋找最佳路徑,且能快速找到。
- 如果 $h(n)$ 大於 $n$ 到終點的實際距離時,不一定能尋找到最佳路徑,但計算速度極快。
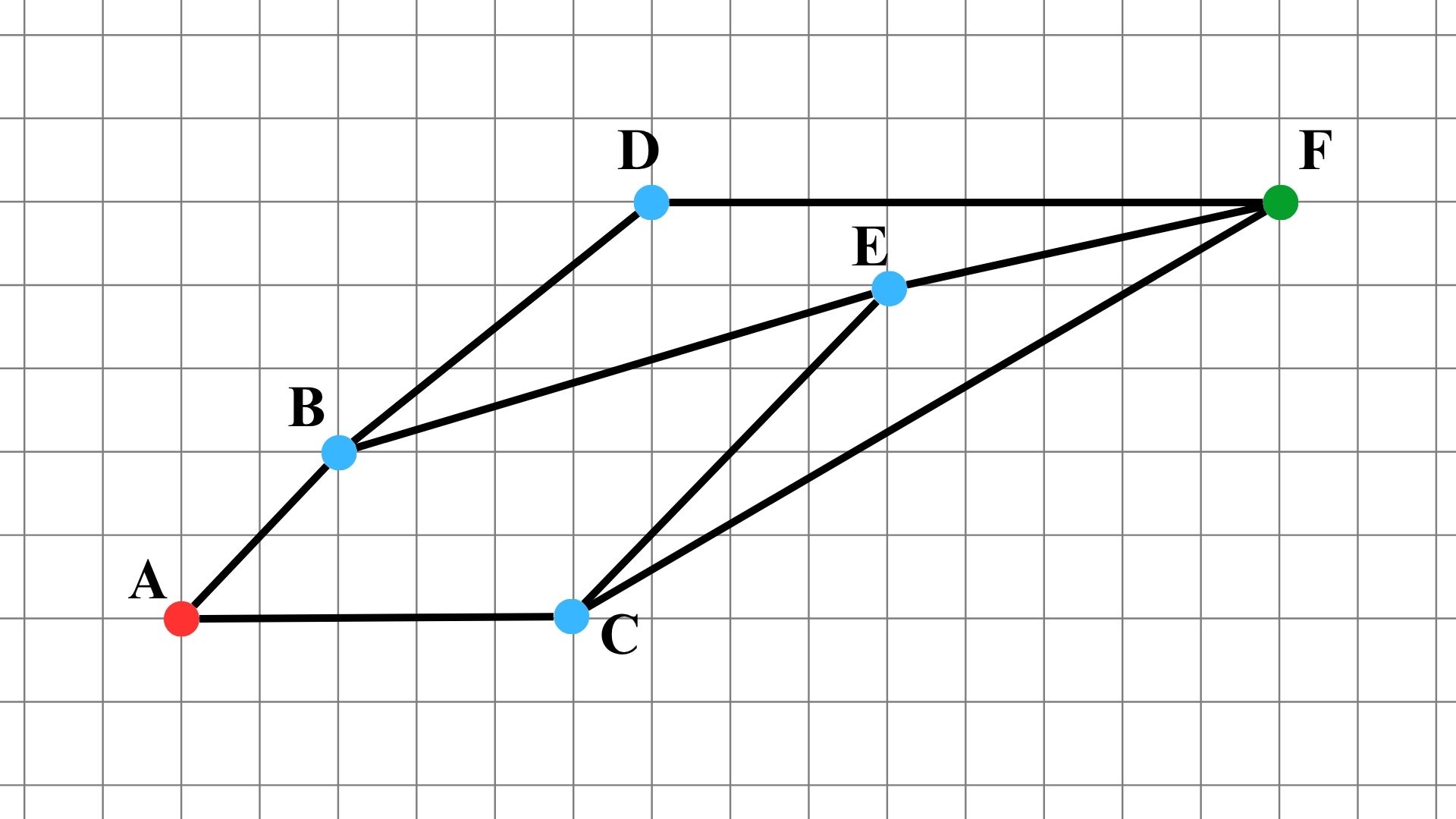
以下舉簡單範例。
如上圖,假設現在有六個地點,依序為 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $F$ 。現在以 $A$ 點為起點, $F$ 點為終點,欲尋找 $A$ 點到 $F$ 點的路徑。
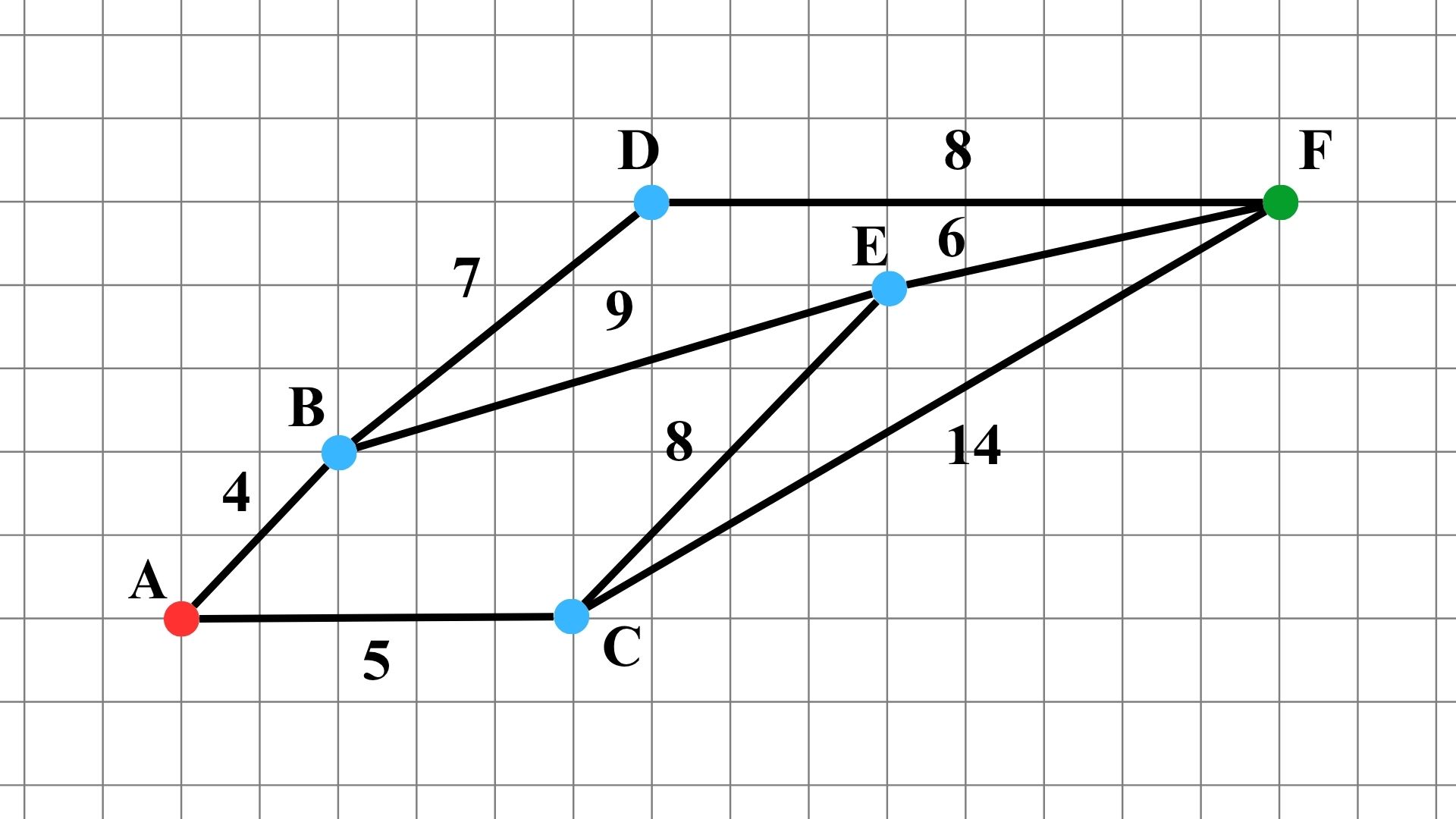
首先,計算各路徑的距離,此處採用曼哈頓距離,如下圖所示。
為了找到從 $A$ 點出發的最佳路徑,以下建立表格用於記錄路徑尋找過程中的前一個地點與計算函式, $f(n)$ 預設為 $\infty$ 。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | $\infty$ | ||||
| B | $\infty$ | ||||
| C | $\infty$ | ||||
| D | $\infty$ | ||||
| E | $\infty$ | ||||
| F | $\infty$ |
因為出發點為 $A$ ,故先標記 $A$ 點,並計算相應的函數。其中, $g(n)$ 為起點經各路徑到各點的距離, $h(n)$ 為各點直接到終點的曼哈頓距離。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | ✓ | 0 | 19 | 19 | |
| B | $\infty$ | ||||
| C | $\infty$ | ||||
| D | $\infty$ | ||||
| E | $\infty$ | ||||
| F | $\infty$ |
接下來,檢查與 $A$ 鄰近且未標記的地點,並計算函數。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | ✓ | 0 | 19 | 19 | |
| B | 4 | 15 | 19 | A | |
| C | 5 | 14 | 19 | A | |
| D | $\infty$ | ||||
| E | $\infty$ | ||||
| F | $\infty$ |
比較 $f(n)$ 並找出最小的。因為 $B$ 與 $C$ 的 $f(n)$ 相同,我們選取其中一個進行標記。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | ✓ | 0 | 19 | 19 | |
| B | ✓ | 4 | 15 | 19 | A |
| C | 5 | 14 | 19 | A | |
| D | $\infty$ | ||||
| E | $\infty$ | ||||
| F | $\infty$ |
接下來,尋找標記點 $B$ 的鄰近且未標記的地點,並計算函數。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | ✓ | 0 | 19 | 19 | |
| B | ✓ | 4 | 15 | 19 | A |
| C | 5 | 14 | 19 | A | |
| D | 11 | 8 | 19 | B | |
| E | 13 | 6 | 19 | B | |
| F | $\infty$ |
現在,比較 $f(n)$ 並找出最小的。因為 $C$ 、 $D$ 、 $E$ 的 $f(n)$ 都為 19 ,這裡選取 $C$ 進行標記。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | ✓ | 0 | 19 | 19 | |
| B | ✓ | 4 | 15 | 19 | A |
| C | ✓ | 5 | 14 | 19 | A |
| D | 11 | 8 | 19 | B | |
| E | 13 | 6 | 19 | B | |
| F | 19 | 0 | 19 | C |
重複標記未被標記的最佳路徑,並更新其相鄰的地點,直到所有地點都被標記。最終可以得到如下表格。
| 地點 | 標記 | $g(n)$ | $h(n)$ | $f(n)$ | 前一個地點 |
|---|---|---|---|---|---|
| A | ✓ | 0 | 19 | 19 | |
| B | ✓ | 4 | 15 | 19 | A |
| C | ✓ | 5 | 14 | 19 | A |
| D | ✓ | 11 | 8 | 19 | B |
| E | ✓ | 13 | 6 | 19 | B |
| F | ✓ | 19 | 0 | 19 | C |
從以上表格,我們不僅可以知道最短路徑距離為 19 ,還能從終點 $F$ 反推最佳路徑到起點 $A$ 。由上表,可以知道最佳路徑為 $$ A \Rightarrow C \Rightarrow F $$
當然,計算地點 $n$ 到終點的函式 $h(n)$ 不一定需要和上述的路徑計算方式都同為曼哈頓距離,也可採用其他計算方式;同理,各地點間的路徑長也可使用其他計算方式,如歐幾里得距離等。採用不同的計算方式,可使 $f(n)$ 函式的值不同,使結果更快被計算出來。
演算法
根據以上範例,可以大致總結 A* 演算法步驟如下:
- 將 $f(n)$ 初始值設為 $\infty$ 。
- 從未標記的地點選擇 $f(n)$ 最小者。
- 標記該地點。
- 計算經該地點的 $g(n)$ 、 $h(n)$ 與 $f(n)$。
- 回到第 2 步並重複執行,直到所有地點都被標記。
結語
A* 演算法是一種結合了戴克斯特拉演算法的最短路徑與貪婪演算法的效率優勢所衍生出的經典演算法。其不僅能有效應用於地圖導航與路線規劃,也常見於迷宮問題、遊戲角色移動、機器人路徑設計等場景。 A* 演算法可依據實際需求對不同路徑設定不同的權重與偏好,讓結果更符合應用情境,例如避開危險區域、偏好行走於設定的道路而非草叢等。
參考資料
A*搜尋演算法。(2025年6月4日)。維基百科,自由的百科全書。2025年7月8日參考自 https://zh.wikipedia.org/zh-tw/A*搜尋演算法
廢物敗類窩囊廢。(2018年5月14日)。【筆記】遊戲中常用的A*最佳路徑演算法。巴哈姆特。2025年7月8日參考自 https://home.gamer.com.tw/creationDetail.php?sn=3988541
小哈片刻。(2022年9月30日)。Trick 27: 承先啟後的路徑搜尋-A*演算法。iT 邦幫忙。2025年7月8日參考自 https://ithelp.ithome.com.tw/articles/10292260
阿祥的開發日常。(2016年7月8日)。A* Algorithm Introduction – 演算法簡介。WordPress。2025年7月8日參考自 https://tedsieblog.wordpress.com/2016/07/08/a-star-algorithm-introduction/
林家慶。(2023年8月4日)。[遊戲引擎研究] A* 演算法實作 (迷宮搜尋路徑) - 2023/8/4 [影片]。Youtube。2025年7月8日參考自 https://youtu.be/A7xLS75gTzY
小哈片刻。(2021年12月9日)。勇者逛地城的必備技能: (科普)A*演算法 [影片]。Youtube。2025年7月8日參考自 https://youtu.be/_B8XV1iIvq8