貝爾曼-福特演算法

封面圖片由 ChatGPT 生成。

前言

為了解決戴克斯特拉演算法中無法計算路徑為負權重的，貝爾曼-福特演算法（Bellman-Ford Algorithm）就此誕生。貝爾曼-福特演算法會對 $V$ 個節點做 $V - 1$ 次鬆弛操作，重複鬆弛所有邊，進而持續改善、找尋最短路徑。

名詞解釋

什麼是鬆弛

鬆弛（Relaxation）就是嘗試使用某一條邊，更新一個節點目前已知的最短距離，如果這條邊可以讓距離變得更短，就更新它。

什麼是負權迴圈

假設現在可以由幾個節點構成一個圈，此圈的總權重為負。則在進行貝爾曼-福特演算法時會無限繞圈，讓距離變得越來越小，甚至趨近負無限，造成無法定義最短路徑。

為什麼是 $|V|-1$ 鬆弛

$V$ 代表圖（Graph）中的頂點（Vertices）數量，無論從任一頂點到另一個頂點，最多只會經過 $|V|-1$ 條邊（$E$ ， Edges）。因此，如果第 $|V|$ 輪如果還能進行鬆弛操作，一定是陷入重複繞圈，表示存在負權迴圈。

運作原理

如上圖，假設現在有六個地點，依序為 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $F$ 。現在以 $A$ 點為起點， $F$ 點為終點，欲尋找 $A$ 點到 $F$ 點的路徑，其中每條路徑都有各自對應的權重，並且有正有負。為簡化問題，此處指定路徑的方向性。

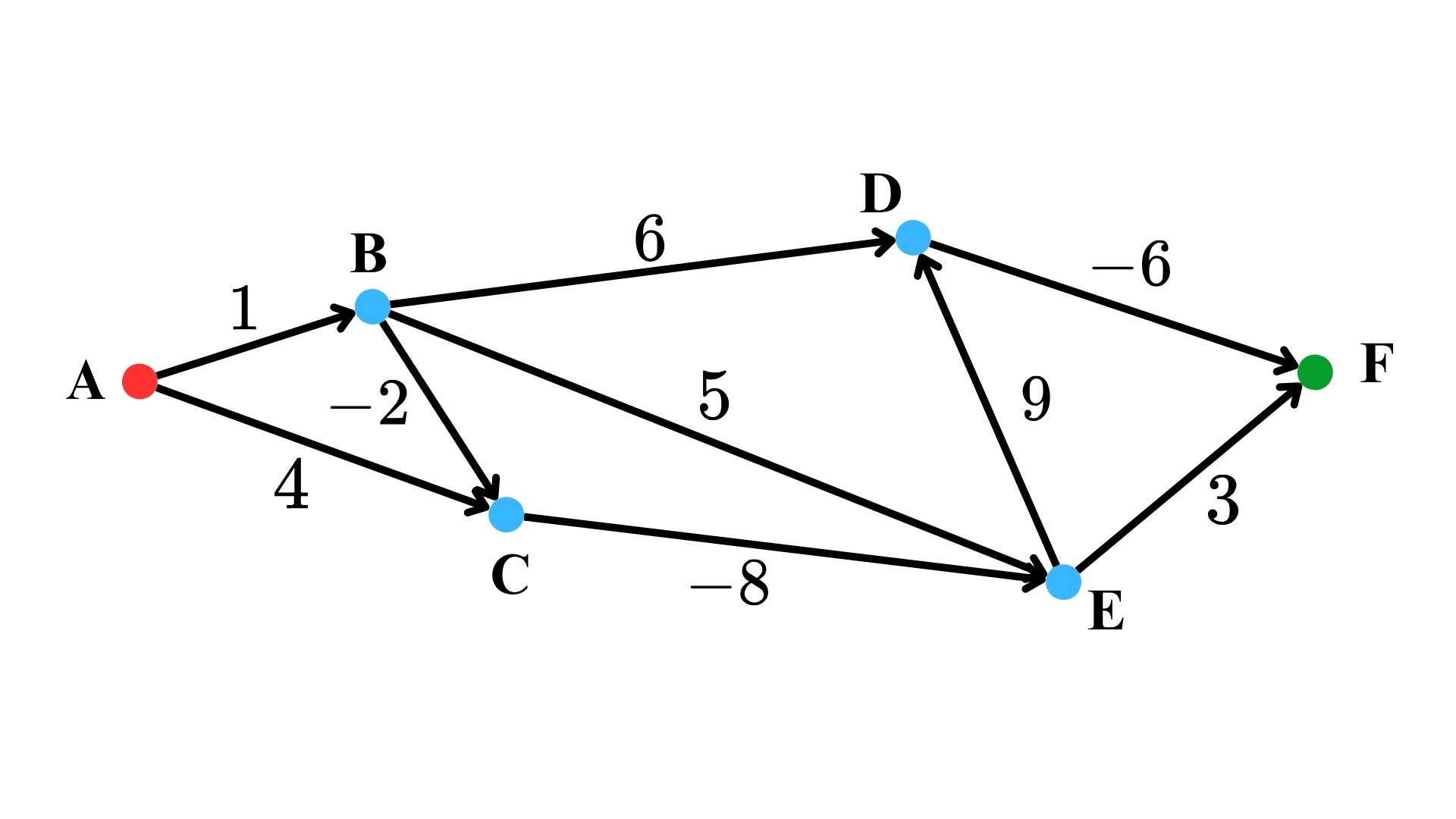
為了找到從 $A$ 點出發到達 $F$ 點的路徑，以下建立表格用於記錄路徑尋找過程中的前一個地點，所有距離的初始值皆為 $\infty$ 。因為總共有 6 個點，因此總共會進行 $|V| - 1 = 6 - 1 = 5$ 輪鬆弛。每一輪都需遍歷每條邊，用於更新每個節點的最短距離。

地點	距離	前一個地點
A	$\infty$
B	$\infty$
C	$\infty$
D	$\infty$
E	$\infty$
F	$\infty$

因為出發點為 $A$ ，因此從 $A$ 開始計算，將 $A$ 點距離標記為 0 。

地點	距離	前一個地點
A	0
B	$\infty$
C	$\infty$
D	$\infty$
E	$\infty$
F	$\infty$

第一輪鬆弛

計算 $A$ 的鄰近點 $B$ 和 $C$ ，因為 $\overline{AB} = 1$ 和 $\overline{AC} = 4$ ，從原點距離計算 $0+1=1$ 、 $0+4=4$ ，都比現在表格中的距離 $\infty$ 還小，因此更新 $B$ 和 $C$ 的距離，並標記前一個地點為 $A$ 。

地點	距離	前一個地點
A	0
B	1	A
C	4	A
D	$\infty$
E	$\infty$
F	$\infty$

接下來檢查與 $B$ 相鄰的點 $C$ 、 $D$ 、 $E$ ，計算如下：

• $B$ 點目前的距離再加上 $\overline{BC}$ ，得到 $1 + (-2) = -1$ ，比目前 $C$ 點距離還要小，因此更新 $C$ 點距離與前一個地點。
• $B$ 點目前的距離再加上 $\overline{BD}$ ，得到 $1 + 6 = 7$ ，比目前 $D$ 點距離還要小，因此更新 $D$ 點距離與前一個地點。
• $B$ 點目前的距離再加上 $\overline{BE}$ ，得到 $1 + 5 = 6$ ，比目前 $E$ 點距離還要小，因此更新 $E$ 點距離與前一個地點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	7	B
E	6	B
F	$\infty$

接下來更新與 $C$ 相鄰的點 $E$ ，計算如下：

• $C$ 點目前的距離再加上 $\overline{CE}$ ，得到 $-1 + (-8) = -9$ ，比目前 $E$ 點距離還要小，因此更新 $E$ 點距離與前一個地點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	7	B
E	-9	C
F	$\infty$

接下來更新與 $D$ 相鄰的點 $F$ ，計算如下：

• $D$ 點目前的距離再加上 $\overline{DF}$ ，得到 $7 + (-6) = 1$ ，比目前 $F$ 點距離還要小，因此更新 $F$ 點距離與前一個地點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	7	B
E	-9	C
F	1	D

接下來更新與 $E$ 相鄰的點 $D$ 、 $F$ ，計算如下：

• $E$ 點目前的距離再加上 $\overline{DE}$ ，得到 $-9 + 9 = 0$ ，比目前 $D$ 點距離還要小，因此更新 $D$ 點距離與前一個地點。
• $E$ 點目前的距離再加上 $\overline{EF}$ ，得到 $-9 + 3 = -6$ ，比目前 $F$ 點距離還要小，因此更新 $F$ 點距離與前一個地點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	0	E
E	-9	C
F	-6	E

$F$ 點是終點，無後續其他點。當所有點都都遍歷過，這一輪鬆弛就結束，可以進行下一輪鬆弛。

第二輪鬆弛

接下來進行第二輪鬆弛。從 $A$ 點開始，與 $A$ 相鄰的點有 $B$ 和 $C$ ，且 $A$ 目前的距離為 0 。因為 $\overline{AB} = 1$ ，且 $A$ 目前的距離再加上 $\overline{AB}$ 就得到 $0 + 1 = 1$ ， 不小於 $B$ 點現有距離 $-4$ ，因此不更新。同理， $C$ 點也是。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	0	E
E	-9	C
F	-6	E

計算出 $A$ 點鄰近的 $B$ 、 $C$ 點不需更新後，現在依序計算其他點，從 $B$ 點開始。 $B$ 點鄰近點為 $C$ 、 $D$ 、 $E$ ，計算如下：

• $B$ 點目前的距離再加上 $\overline{BC}$ ，得到 $1 + (-2) = -1$ 不小於 $C$ 點現有距離 -1 ，因此不更新 $C$ 點。
• $B$ 點目前的距離再加上 $\overline{BD}$ ，得到 $1 + 6 = 7$ 不小於 $D$ 點現有距離 0 ，因此不更新 $D$ 點。
• $B$ 點目前的距離再加上 $\overline{BE}$ ，得到 $1 + 5 = 6$ 不小於 $E$ 點現有距離 -9 ，因此不更新 $E$ 點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	0	E
E	-9	C
F	-6	E

接下來更新 $C$ 點鄰近的點 $E$ 。 $C$ 點目前距離為 $-1$ ，對 $\overline{CE} = -8$ 操作後，得到 $E$ 點距離為 $-1 + (-8) = -9$ ，因此不更新 $E$ 點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	0	E
E	-9	C
F	-6	E

接下來更新 $D$ 點鄰近的點 $F$ 。 $D$ 點目前距離為 $0$ ，對 $\overline{DF} = -6$ 操作後，得到 $F$ 點距離為 $0 + (-6) = -6$ ，因此不更新 $F$ 點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	0	E
E	-9	C
F	-6	E

最後更新 $E$ 點鄰近的點 $D$ 、 $F$ ，計算如下：

• $E$ 點目前的距離再加上 $\overline{DE}$ ，得到 $-9 + 9 = 0$ 不小於 $D$ 點現有距離 0 ，因此不更新 $D$ 點。
• $E$ 點目前的距離再加上 $\overline{EF}$ ，得到 $-9 + 3 = -6$ 不小於 $F$ 點現有距離 -6 ，因此不更新 $F$ 點。

地點	距離	前一個地點
A	0
B	1	A
C	-1	B
D	0	E
E	-9	C
F	-6	E

第三輪鬆弛

由於在第二輪中，所有的點距離已經無再變動。因此，第三、四、五倫鬆弛已經沒有計算的必要。

若有張圖在計算完 $|V| - 1$ 輪後， 在第 $|V|$ 輪還能夠繼續鬆弛，代表該圖存在負權迴圈，會出現無限次鬆弛的情形，無法正確求出最短路徑，應該停止計算並調整路徑，或更換演算法。

路徑

經過以上演算，可以得到 $A$ 點到各點路徑為

$A \to B$ $$ A \Rightarrow B, $$

$A \to C$ $$ A \Rightarrow B \Rightarrow C, $$

$A \to D$ $$ A \Rightarrow B \Rightarrow C \Rightarrow E \Rightarrow D, $$

$A \to E$ $$ A \Rightarrow B \Rightarrow C \Rightarrow E, $$

$A \to F$ $$ A \Rightarrow B \Rightarrow C \Rightarrow E \Rightarrow F, $$

演算法

根據以上範例，可以總結貝爾曼-福特演算法步驟如下：

1. 初始化所有距離，將所有節點 $u$ 的最短距離 $dist[u]$ 設為 $\infty$，起點距離設為 0 。
2. 進行第 $i$ 輪鬆弛。
3. 設定愈計算的該條路徑長為 $w$ ，若更新後的最短距離 $dist[u] + w$ 小於原最短距離 $dist[v]$，則更新 $dist[v] = dist[u] + w$ ，並記錄前一個地點 $pre[v] = u$ 。
4. 回到第 3 步，直到完成一輪所有邊的鬆弛。
5. 回到第 2 步，直到 $i \leq |V| - 1$ 。
6. 進行第 $|V|$ 輪鬆弛，若仍有任何邊滿足 $dist[u] + w < dist[v]$ ，則代表圖中存在負權迴圈，此時演算法應終止。
7. 輸出最短路徑結果。

結語

貝爾曼-福特演算法是一個簡單且強大的最短路徑演算法，能處理戴克斯特拉演算法無法處理的負權重問題，在邊數不多或需要處理負權邊的問題中非常實用。

參考資料

• 貝爾曼-福特演算法。（2024年11月14日）。維基百科，自由的百科全書。2025年7月17日參考自 https://zh.wikipedia.org/zh-tw/贝尔曼-福特算法

• 波波微课。（2025年4月1日）。Bellman-Ford最短路径算法 [影片]。Youtube。2025年7月18日參考自 https://youtu.be/YklWOOAR6rs