常用的距離度量方法

Josh

發佈於 2025-06-20 更新於 2025-06-28 約 3858 字預計閱讀 8 分鐘次閱讀

封面圖片由 ChatGPT 生成。

前言

如何計算距離是現今統計分析中重要的一個環節，選擇不同的距離度量方式對於統計分析方法可能會產生不同的結果。以下介紹常用的距離度量方法。

歐幾里得距離

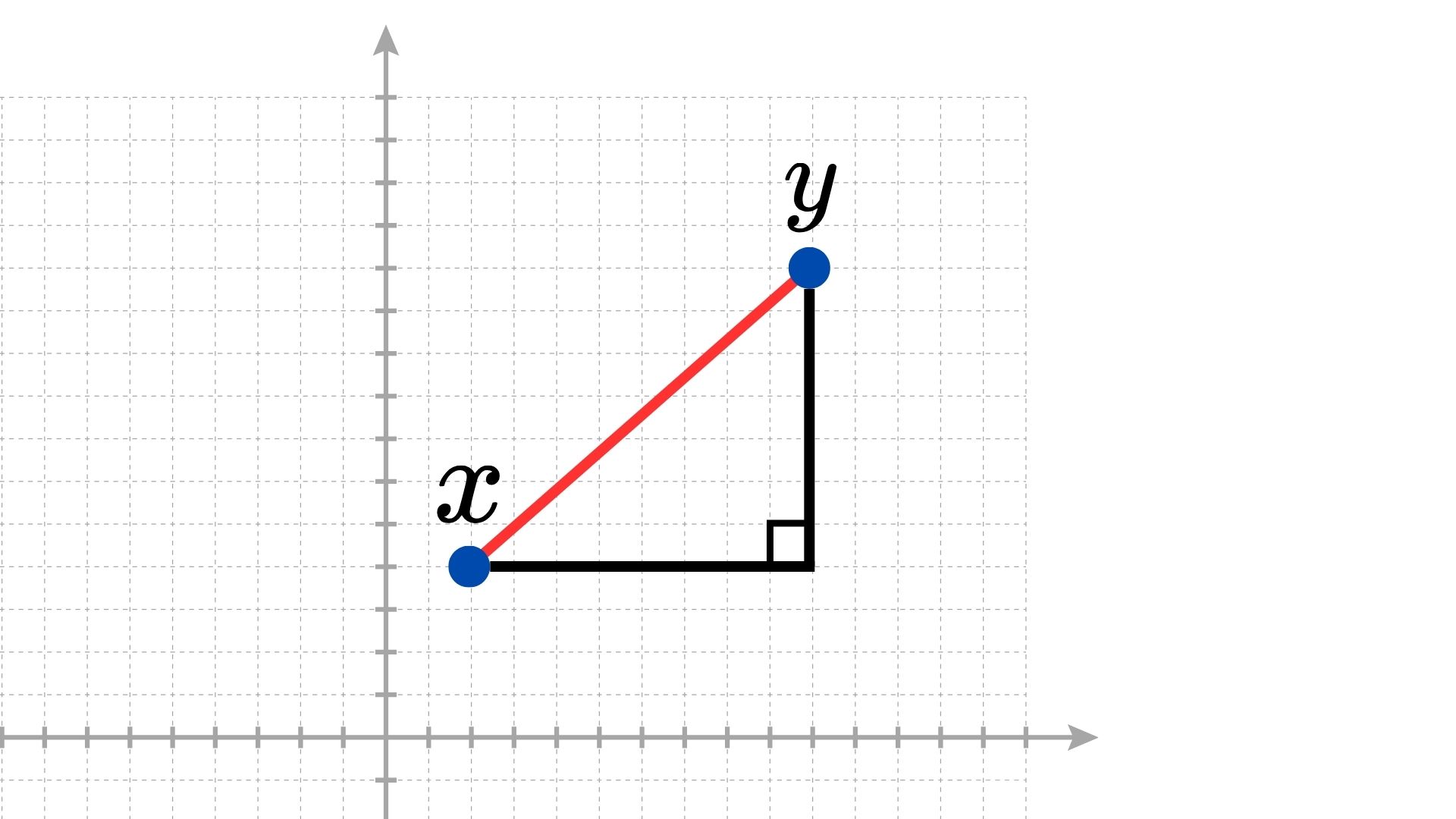
歐幾里得距離（Euclidean Distance），又稱為歐式距離，是最常見的距離度量方法之一，又稱為 $L_2$ 距離，其指的是兩點間所連線段的直線距離。

https://raw.githubusercontent.com/Josh-test-lab/website-assets-repository/refs/heads/main/posts/Common%20Distance%20Measures/Euclidean%20Distance.jpg — 歐幾里得距離。

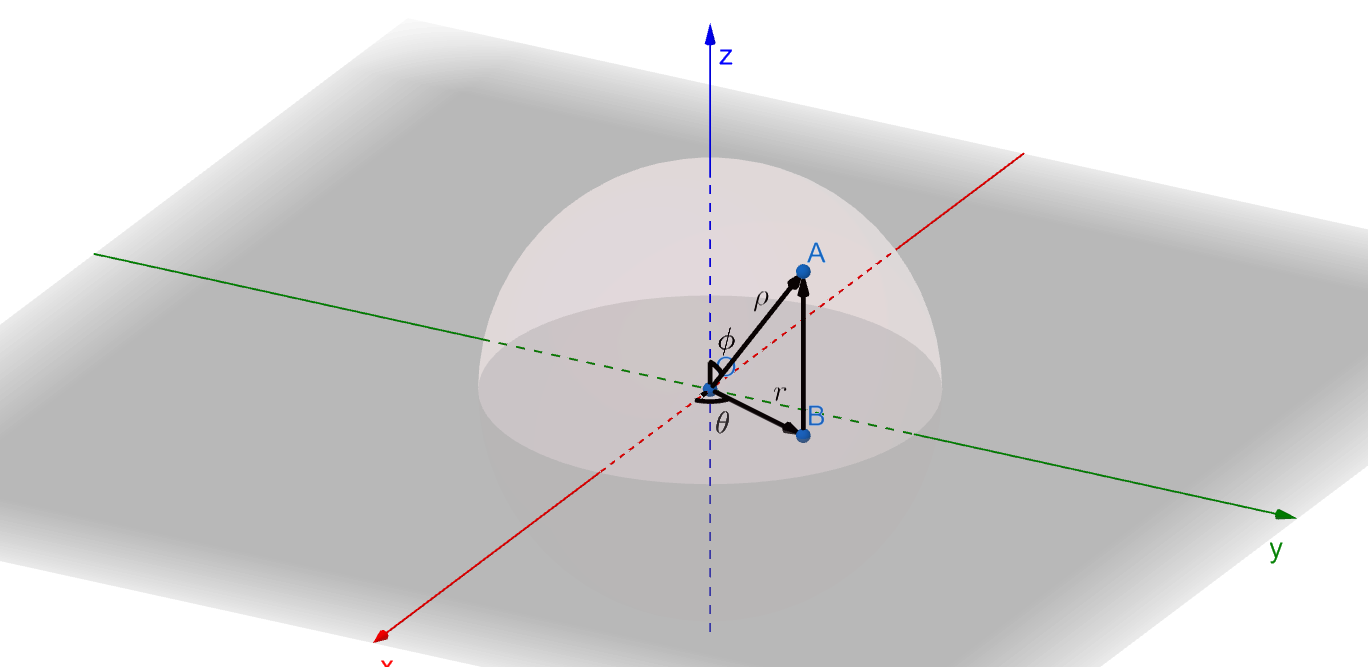
如上圖，假設

$$ \begin{align*} & x=(x_1 , \cdots , x_n); \\ & y=(y_1 , \cdots , y_n). \end{align*} $$

則兩點間的距離 $d(x, y)$ 可以表示為

$$ \begin{align*} d(x,y) & = \sqrt{(x_1-y_1)^2 +(x_2-y_2)^2 + \cdots +(x_n-y_n)^2} \\ & = \sqrt{\sum_{i = 1}^n (x_i - y_i)^2}. \end{align*} $$

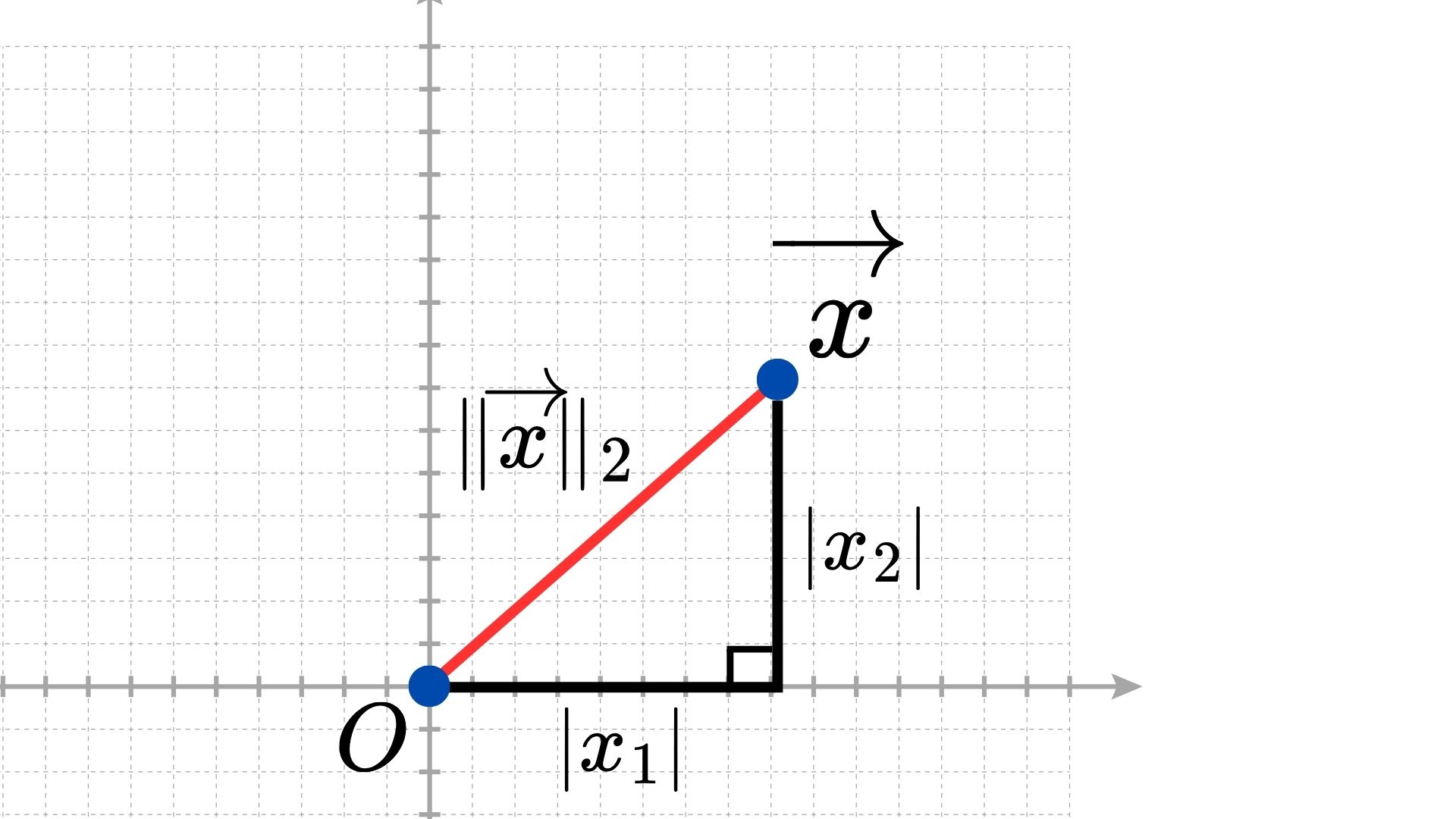
同時，我們也可以計算由原點 $(0, \cdots, 0)$ 至 $x$ 點的向量，如下圖：

其中， $x$ 的向量表示為 $\overrightarrow{x}$ 。該向量長度範數（Norm），又稱作 $L_2$ 範數（$L_2$ Norm），則表示為 $\|x\|_2$，計算公式如下： $$ \|\vec{x}\|_2 = \sqrt{|x_1|^2 + \cdots + |x_n|^2} $$

範例

假設存在兩點

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其歐式距離為

$$ \sqrt{(1 - 1)^2 + (2 - 0)^2 + (3 - 6)^2} = \sqrt{13} \approx 3.61 $$

曼哈頓距離

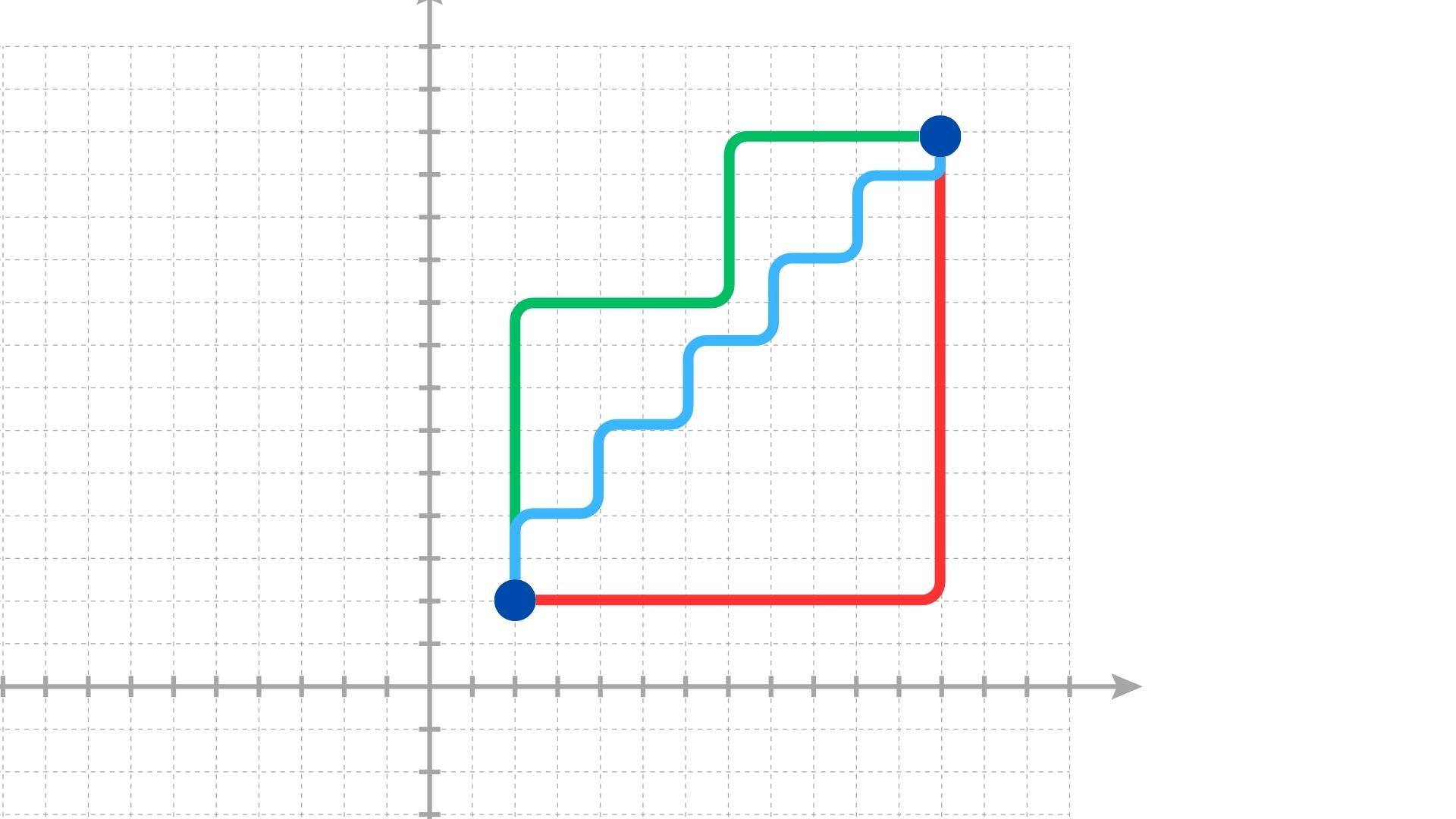
曼哈頓距離（Manhattan Distance）也稱作城市街區距離或 $L_1$ 距離，指的是只沿坐標軸方向移動的距離總和。最早是在探討一座擁有許多大型方型街區的城市，如美國紐約市的曼哈頓區，之中最短的行車路徑。

https://raw.githubusercontent.com/Josh-test-lab/website-assets-repository/refs/heads/main/posts/Common%20Distance%20Measures/Manhattan%20Distance.jpg — 曼哈頓距離。

如上圖，紅、藍、綠線皆表示兩點間的曼哈頓距離，所有線段都擁有一樣的長度。

假設存在兩點

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩點間的距離 $d(x, y)$ 可以表示為

$$ \begin{align*} d(x, y) & = |x_1 - y_1| + |x_2 - y_2| + \cdots + |x_n - y_n| \\ & = \sum_{i = 1}^n |x_i - y_i|. \end{align*} $$

範例

假設存在兩點

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其曼哈頓距離為

$$ |1 - 1| + |2 - 0| + |3 - 6| = 5 $$

柴比雪夫距離

柴比雪夫距離（Chebyshev Distance）又稱為棋盤距離（Chessboard Distance）、 $L_\infty$ 距離，指兩點在任一維度上的最大差距。

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

西洋棋盤，2025 年 6 月 27 日擷取自維基百科。

如上圖，定義每格格子邊長為 1 ，則對於任意一格，如圖中的王（king）♔，其八個相鄰格子距離為 1 ，再往外一圈為 2 ，以此類推。

假設存在兩點

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩點間的距離 $d(x, y)$ 可以表示為

$$ \begin{align*} d(x, y) & = \max(|x_1 - y_1|, |x_2 - y_2|, \cdots, |x_n - y_n|) \\ & = \max_i(|x_i - y_i|). \end{align*} $$

而柴比雪夫距離其實是 $L_k$ 範數在 $k \to \infty$ 時的極限形式。$L_k$ 範數的定義如下：

$$ \|w\|_k = \left( \sum_{i=1}^n |w_i|^k \right)^{1/k}. $$

假設存在兩點

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩點間的距離向量可以表示為

$$ \left( \sum_{i=1}^n |x_i - y_i|^k \right)^{1/k}. $$

當 $k \to \infty$ 時，我們可以得到兩點間的距離為

$$ \begin{align*} d(x, y) & = \lim_{k \to \infty} \left( \sum_{i=1}^n |x_i - y_i|^k \right)^{1/k} \\ & = \max_i(|x_i - y_i|), \end{align*} $$

即為柴比雪夫距離。

這個極限的證明如下：

證明

設 $a_i = |x_i - y_i|$ ，令 $a = \max_i \{a_i\}$ ，則：

上界：
$$ \sum_{i=1}^n a_i^k \le n \cdot a^k \quad \Rightarrow \quad \left( \sum_{i=1}^n a_i^k \right)^{1/k} \le a \cdot n^{1/k} $$
下界：
$$ \sum_{i=1}^n a_i^k \ge a^k \quad \Rightarrow \quad \left( \sum_{i=1}^n a_i^k \right)^{1/k} \ge a $$

由夾擠定理（Squeeze Theorem）得到：

$$ \begin{align*} & \qquad a \le \left( \sum_{i=1}^n a_i^k \right)^{1/k} \le a \cdot n^{1/k} \\ & \Rightarrow \lim_{k \to \infty} \left( \sum_{i=1}^n a_i^k \right)^{1/k} = a = \max_i \{a_i\}, && \text{when } \lim_{k \to \infty} n^{1/k} = 1. \end{align*} $$

所以，當 $k \to \infty$ 時， $L_k$ 範數的極限正是柴比雪夫距離，即：

$$ d(x, y) = \max_i |x_i - y_i|. $$

提醒

當 $k$ 越來越大，只有最大的一項 $|x_i - y_i|^k$ 對總和有決定性的影響，其它項相對趨近於 0，因此結果會趨近最大項的絕對值。

範例

假設存在兩點

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其柴比雪夫距離為

$$ \max \left( |1 - 1| + |2 - 0| + |3 - 6| \right) = 3 $$

明可夫斯基距離

明可夫斯基距離（Minkowski Distance），又稱為 $L_k$ 距離，是歐幾里得距離與曼哈頓距離的廣義形式。

假設存在兩點

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩點間的距離向量可以表示為

$$ d(x, y) = \left( \sum_{i=1}^n |x_i - y_i|^k \right)^{1/k}. $$

同時，我們也可以發現以下幾點

當 $k \to 1$ 時 $L_k$ 範數會退化成曼哈頓距離（$L_1$ 距離） $$ \| x - y \|_1 = \sum_{i=1}^n |x_i - y_i|. $$
當 $k \to 2$ 時 $L_k$ 範數會退化成歐幾里得距離（$L_2$ 距離） $$ \| x - y \|_2 = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}. $$
當 $k \to \infty$ 時 $L_k$ 範數會變成柴比雪夫距離（$L_\infty$ 距離） $$ \| x - y \|_\infty = \max_i(|x_i - y_i|). $$

範例

假設存在兩點

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其明可夫斯基距離為

$$ \left( |1 - 1|^3 + |2 - 0|^3 + |3 - 6|^3 \right)^{1/3} = \sqrt[3]{35} \approx 3.27 $$

坎培拉距離

坎培拉距離（Canberra Distance）是向量空間中點與點之間距離的數值度量，坎培拉距離對於小數值的差異較為敏感，強調數值間的相對差異而不是絕對差異。常用於檢測微小但相對明顯的變化。

假設存在兩點

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩點間的距離向量可以表示為

$$ d(x, y) = \sum_{i=1}^{n} \frac{|x_i - y_i|}{|x_i| + |y_i|} $$

範例

假設存在兩點

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其坎培拉距離為

$$ \frac{|1 - 1|}{|1| + |1|} + \frac{|2 - 0|}{|2| + |0|} + \frac{|3 - 6|}{|3| + |6|} = \frac{4}{3} \approx 1.33 $$

餘弦距離

在講餘弦距離（Cosine Distance）前，不得不提到餘弦相似性（Cosine Similarity）。

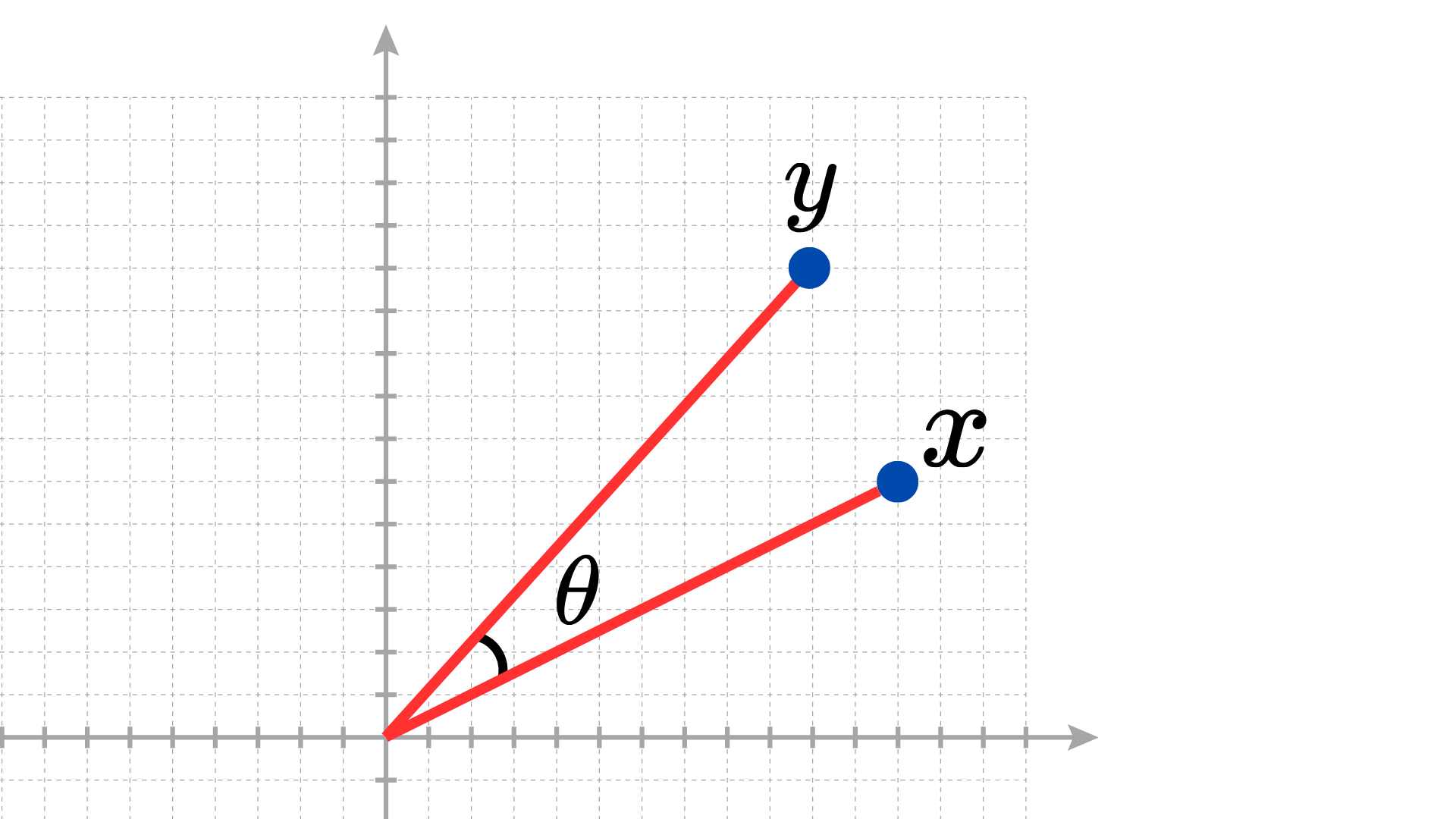
餘弦相似性是透過計算由任意兩點與原點所組成的向量的夾角，判斷兩向量間的餘弦值作為相似性。由於餘弦值的計算可作用於實數空間 $\mathbb{R}$ ，因此餘弦相似性的值域為 $(-1, 1)$ ；但通常在計算兩點間的距離時，常作用於正實數空間 $\mathbb{R}^+$ ，故值域通常為 $(0, 1)$ 。

https://raw.githubusercontent.com/Josh-test-lab/website-assets-repository/refs/heads/main/posts/Common%20Distance%20Measures/Cosine%20Distance.png — 餘弦距離。

假設存在兩點

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩點間的餘弦相似性為

$$ \begin{align*} \cos(\theta) & = {x \cdot y \over \|x\| \|y\|} \\ & = \frac{ \sum\limits_{i=1}^{n}{x_i \times y_i} }{ \sqrt{\sum\limits_{i=1}^{n}{(x_i)^2}} \times \sqrt{\sum\limits_{i=1}^{n}{(y_i)^2}} }. \end{align*} $$

在餘弦相似性中，兩點與原點組成的向量的夾角若越小，則越趨近於 1 ；反之，則趨近於 0 或 -1 。

而餘弦距離的計算方式為

$$ \text{餘弦距離} = 1 - \text{餘弦相似性}, $$

也就是

$$ d(x, y) = 1 - \cos(\theta), $$

其中， $\theta$ 為 $x$ 和 $y$ 與原點組成向量的夾角。

範例

假設存在兩點

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其餘弦距離為

$$ 1 - \frac{1 \times 1 + 2 \times 0 + 3 \times 6}{\sqrt{1^2 + 2^2 + 3^2} \times \sqrt{1^2 + 0^2 + 6^2}} = 1 - \frac{19}{\sqrt{14} \times \sqrt{37}} \approx 0.17 $$

布雷-柯蒂斯相異度

布雷-柯蒂斯相異度（Bray–Curtis Dissimilarity）是生物學、生態學、分類學中常用的距離量度方法，用於衡量兩個樣本在物種組成或特徵分佈上的差異程度，其值域介於 $(0, 1)$ 。其中， 0 表示完全相同； 1 表示完全不同。

其性質如下：

若在某一維度上 $x_i = y_i = 0$ ，該維度不影響計算結果，適用於稀疏向量資料。
不符合距離公理，因此是它是「相異度」而非嚴格定義的「距離」。

假設存在兩樣本

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩樣本間的相似度可以表示為

$$ \begin{align*} \text{Bray–Curtis}(x, y) & = \frac{\sum_{i=1}^{n} |x_i - y_i|}{\sum_{i=1}^{n} (x_i + y_i)} \\ & = 1 - \frac{2 \sum_{i=1}^{n} \min(x_i, y_i)}{\sum_{i=1}^{n} (x_i + y_i)}. \end{align*} $$

範例

假設存在兩樣本

$$ \begin{align*} & x=(1, 2, 3); \\ & y=(1, 0, 6). \end{align*} $$

則其布雷-柯蒂斯相異度為

$$ \frac{|1 - 1| + |2 - 0| + |3 - 6|}{(1 + 1) + (2 + 0) + (3 + 6)} = \frac{5}{13} \approx 0.38 $$

漢明距離

漢明距離（Hamming Distance）是指兩個等長字串對應位置的不同字元的個數。也就是說，將一個字串變換成另外一個字串所需要替換的字元數量。需要注意的是，漢明距離不能用於連續數值向量。

假設存在兩字串

$$ \begin{align*} & x=(x_1, \cdots, x_n); \\ & y=(y_1, \cdots, y_n). \end{align*} $$

則兩字串間的漢明距離為

$$ d(x, y) = \sum_{i=1}^{n} \delta(x_i, y_i), $$

其中，$ \delta(x_i, y_i) = \begin{cases} 0, & \text{if } x_i = y_i; \\ 1, & \text{if } x_i \ne y_i. \end{cases} $

範例

假設有三筆等長數據如下：

第一組為 $x = 1234567$
第二組為 $y = 7654321$
第三組為 $z = 1234321$

我們可以得到各數據間的漢明距離為

組合	比較	漢明距離
$d(x, y)$	第一組：1234567 第二組：7654321	6
$d(x, z)$	第一組：1234567 第三組：1234321	3
$d(y, z)$	第二組：7654321 第三組：1234321	3

其中，以紅色標記者為對應位置不同的字元。

雅卡爾距離

提到雅卡爾距離（Jaccard Distance）就不得不提到雅卡爾指數（Jaccard Index）了。

雅卡爾指數又稱為雅卡爾相似係數（Jaccard similarity coefficient），是用於比較兩有限集合相似度的一個方法。其定義如下

假設存在兩個有限集合 $A \in \mathbb{R}^m$ 、 $B \in \mathbb{R}^n$ ，則

$$ \begin{align*} \text{Jaccard Index} = J(A, B) & = \frac{|A \cap B|}{|A \cup B|} \\ & = \frac{|A \cap B|}{|A| + |B| - |A \cap B|}, \end{align*} $$

其中， $0 \le J(A, B) \le 1$ 。

由此，可以衍伸出雅卡爾距離

$$ d(A, B) = 1 - \frac{|A \cap B|}{|A \cup B|} $$

範例

假設存在兩集合

$$ \begin{align*} & A=\{1, 2, 3\}; \\ & B=\{1, 0, 6\}. \end{align*} $$

則其雅卡爾距離為

$$ 1 - \frac{|{1}|}{|{0,1,2,3,6}|} = 1 - \frac{1}{5} = 0.8 $$

結語

不同的距離度量方法適用於不同的資料型態與應用情境，更是衡量資料間關係的核心工具。距離不只代表點與點之間的間隔，也可能代表兩集合間的相似度，為模型計算帶來不一樣的視角，捕捉到更有意義的模式與差異。

參考資料

歐幾里得距離。（2025年3月9日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/欧几里得距离
曼哈頓距離。（2023年12月12日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/曼哈頓距離
切比雪夫距離。（2024年4月16日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/切比雪夫距离
Minkowski distance。（2025年6月20日）。維基百科，自由的百科全書。2025年6月28日參考自 https://en.wikipedia.org/wiki/Minkowski_distance
Canberra distance。（2024年3月30日）。維基百科，自由的百科全書。2025年6月28日參考自 https://en.wikipedia.org/wiki/Canberra_distance
餘弦相似性。（2025年1月15日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/余弦相似性
布雷-柯蒂斯相異度。（2021年9月26日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/布雷-柯蒂斯相异度
漢明距離。（2025年5月30日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/汉明距离
雅卡爾指數。（2023年8月30日）。維基百科，自由的百科全書。2025年6月28日參考自 https://zh.wikipedia.org/zh-tw/雅卡尔指数

目錄

常用的距離度量方法

前言

歐幾里得距離

曼哈頓距離

柴比雪夫距離

明可夫斯基距離

坎培拉距離

餘弦距離

布雷-柯蒂斯相異度

漢明距離

雅卡爾距離

結語

參考資料

相關文章