資料集探索與分析 #2
多變量分析 final project 。

封面圖片為 ChatGPT 生成的資料集探索與分析的圖片,提示詞為 “A digital illustration in a 16:9 aspect ratio, showing a young male data analyst working in a modern high-tech office, analyzing a large dataset on a widescreen monitor. The screen displays various data visualizations: bar charts, scatter plots, histograms, and data tables. The interface is sleek and futuristic, with turquoise and blue tones, glowing UI elements, and a clear emphasis on Dataset Exploration and Analysis” 。
前言
本次使用的資料集取自 kaggle 上由 Adil Shamim 所提供的數學學生成績資料集。此資料集源自 UCI 機器學習庫,最初由 P. Cortez 和 A. Silva 在題為「使用資料探勘預測中學學生成績」的研究中提出。此資料集是葡萄牙波爾圖舉行的第五屆 FUBUTEC 2008 會議上提出的研究的一部分。此資料集的 G1, G2, G3, absences 是直接來自學校提供之資料,其他變數則是透過問卷調查蒐集。
本文將以 Python 作為資料分析的程式語言,且目標為找出會影響學期成績的變數 G3 。
資料集
變數說明
此資料集共有 399 筆資料, 33 個變數。變數說明如下:
| 變數 | 說明 | 資料類型 | 範圍 |
|---|---|---|---|
school | 學生學校 | 二元型 | GP - Gabriel Pereira MS - Mousinho da Silveira |
sex | 學生的性別 | 二元型 | F - 女性 M - 男性 |
age | 學生年齡 | 數值型 | 15 到 22 |
address | 學生家庭住址類型 | 二元型 | U - 城市 R - 鄉村 |
famsize | 家庭規模 | 二元型 | LE3 - 小於等於 3 GT3 - 大於 3 |
Pstatus | 父母的同居狀態 | 二元型 | T - 同居 A - 分開 |
Medu | 母親教育程度 | 數值型 | 0 - 無 1 - 4 年級 2 - 5 至 9 年級 3 - 中學教育 4 - 高等教育 |
Fedu | 父親教育程度 | 數值型 | 0 - 無 1 - 4 年級 2 - 5 至 9 年級 3 - 中學教育 4 - 高等教育 |
Mjob | 母親的工作 | 名目型 | teacher - 教師 health - 醫療相關 services - 公務員 at_home - 在家工作 other - 其他 |
Fjob | 父親的工作 | 名目型 | teacher - 教師 health - 醫療相關 services - 公務員 at_home - 在家工作 other - 其他 |
reason | 選擇學校的原因 | 名目型 | home - 離家近 reputation - 學校聲望 course - 課程偏好 other - 其他 |
guardian | 監護人 | 名目型 | mother - 母親 father - 父親 other - 其他 |
traveltime | 通勤時間 | 數值型 | 1 - < 15 分鐘 2 - 15 到 30 分鐘 3 - 30 分鐘到 1 小時 4 - > 1 小時 |
studytime | 每週學習時間 | 數值型 | 1 - < 2 小時 2 - 2 到 5 小時 3 - 5 到 10 小時 4 - > 10 小時 |
failures | 課程失敗次數 | 數值型 | 0 到 3;4 表示超過 3 次 |
schoolsup | 額外教育支持 | 二元型 | yes no |
famsup | 家庭教育支持 | 二元型 | yes no |
paid | 額外付費課程 | 二元型 | yes no |
activities | 課外活動 | 二元型 | yes no |
nursery | 是否上過幼兒園 | 二元型 | yes no |
higher | 是否想上大學 | 二元型 | yes no |
internet | 家中是否有網路 | 二元型 | yes no |
romantic | 是否有戀愛關係 | 二元型 | yes no |
famrel | 家庭關係品質 | 數值型 | 1(非常差)到 5(非常好) |
freetime | 放學後空閒時間 | 數值型 | 1(非常少)到 5(非常多) |
goout | 與朋友外出頻率 | 數值型 | 1(非常少)到 5(非常多) |
Dalc | 平日酒精消費量 | 數值型 | 1(非常少)到 5(非常多) |
Walc | 週末酒精消費量 | 數值型 | 1(非常少)到 5(非常多) |
health | 健康狀況 | 數值型 | 1(非常差)到 5(非常好) |
absences | 缺席次數 | 數值型 | 0 到 93 |
G1 | 第一階段成績 | 數值型 | 0 到 20 |
G2 | 第二階段成績 | 數值型 | 0 到 20 |
G3 | 最終成績 | 數值型 | 0 到 20 |
資料集
以下使用 Python 作為資料分析的程式語言,資料集原始內容如下:
| index | school | sex | age | address | famsize | Pstatus | Medu | Fedu | Mjob | Fjob | famrel | freetime | goout | Dalc | Walc | health | absences | G1 | G2 | G3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | GP | F | 18 | U | GT3 | A | 4 | 4 | at_home | teacher | 4 | 3 | 4 | 1 | 1 | 3 | 6 | 5 | 6 | 6 |
| 1 | GP | F | 17 | U | GT3 | T | 1 | 1 | at_home | other | 5 | 3 | 3 | 1 | 1 | 3 | 4 | 5 | 5 | 6 |
| 2 | GP | F | 15 | U | LE3 | T | 1 | 1 | at_home | other | 4 | 3 | 2 | 2 | 3 | 3 | 10 | 7 | 8 | 10 |
| 3 | GP | F | 15 | U | GT3 | T | 4 | 2 | health | services | 3 | 2 | 2 | 1 | 1 | 5 | 2 | 15 | 14 | 15 |
| 4 | GP | F | 16 | U | GT3 | T | 3 | 3 | other | other | 4 | 3 | 2 | 1 | 2 | 5 | 4 | 6 | 10 | 10 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | .. | .. | .. |
| 394 | MS | M | 19 | U | LE3 | T | 1 | 1 | other | at_home | 3 | 2 | 3 | 3 | 3 | 5 | 5 | 8 | 9 | 9 |
| 395 | MS | M | 18 | U | GT3 | T | 4 | 4 | teacher | services | 5 | 3 | 2 | 1 | 2 | 4 | 0 | 8 | 7 | 7 |
| 396 | MS | M | 17 | U | GT3 | T | 4 | 4 | teacher | services | 5 | 3 | 2 | 1 | 2 | 4 | 0 | 8 | 7 | 7 |
| 397 | MS | M | 19 | U | GT3 | T | 4 | 4 | teacher | other | 5 | 3 | 2 | 1 | 2 | 4 | 0 | 8 | 7 | 7 |
| 398 | MS | M | 18 | U | GT3 | T | 4 | 4 | teacher | at_home | 5 | 3 | 2 | 1 | 2 | 4 | 0 | 8 | 7 | 7 |
原資料長條圖
接下來,為了能更好的處理資料,這裡先繪製各變數長條圖,讓我們能從圖中獲取各變數的一些基本資訊。
由圖中,我們可以發現:
- 各年齡的人數有些許不同,以 15 至 18 歲居多。若以臺灣的標準來看,這份資料應以高中生居多。
- 年齡存在 20、21、22 等年紀,推測有可能是留級生或有特殊因素的學生。
- 學生最少的每周學習時間約落於 2 小時左右。
- 學生放學後的空閒時間、第一階段成績、第二階段成績與最終成績呈現類似常態分布。
- 缺席次數、平日酒精消費量與週末酒精消費量呈現右偏態。
- 家庭關係品質與當前健康狀況呈現左偏態。
- 父母工作以其他與公務員居多。
- 男女比例差不多。
資料清理
為了順利分析這筆資料,我們首先將類別型資料分類,指定為因子(factor)或獨熱編碼(one-hot encoding),同時將變數分組與指定要預測的變數 G3。
| 組別 | 變數 |
|---|---|
support | schoolsup, famsup, paid |
family | address, famsize, Pstatus, guardian, traveltime, famrel |
parents | Medu, Fedu, Mjob, Fjob |
performance | failures, studytime, absences |
alcohol | Dalc, Walc, health |
after_class | activities, freetime, goout |
school_choice | reason, nursery, higher |
score | G1, G2, G3 |
| |
接下來,為了方便資料處理,這裡將要轉換為因子的類別型變數依照弱至強的方式進行排列,要使用獨熱編碼的變數因無強弱之分,則盡量將各變數內的順序調整至一致,方便後面畫圖檢查。
在先前的長條圖中,我們發現 MS 這間學校的資料量過少,在進行資料分析時可能會因某校資料量較大而造成分析結果偏向某校,造成偏誤。因此,此處移除資料量較少的 MS 學校,並僅分析 GP 學校。
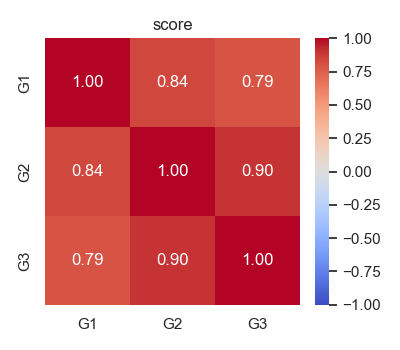
同時, G1 、 G2 與 G3 皆是對學生學期成績評估的總結性評量(summative assessment),這些考試結果都用於評估學生在各階段中的學習成果,此後將繪製三者間的相關係數圖,證明三者存在強烈的相關性。為了分析並找出會影響學生學期成績的變數,此處將原始資料變數另存,並移除 G1 與 G2 ,將 G3 作為需要進行預測的目標。
資料清理後長條圖
以下是經過資料清理後的長條圖,在將 MS 學校的資料移除後,剩下的資料雖大致相同,但也能看出與原資料集的差異。而部分資料由於已從類別型變數被轉換成數值型,因此皆呈現數值。
而以下長條圖也能完整地顯示出 GP 學校的資訊。
相關係數矩陣與散佈圖
我們可以藉由找出相關係數矩陣,判斷變數兩兩間的關係。或是更進階的,繪製相關係數矩陣圖。在下圖中,顏色越紅代表越接近高度正相關;反之,顏色越藍代表越接近高度負相關。
在下圖中,我們可以很明確地看到 G1 、 G2 與 G3 之間有很強烈的相關性。這也是我們為什麼要將 G1 與 G2 從資料集中移除,因為這會使資料分析時的結果總是偏向 G1 、 G2 ,而看不出其他變數與 G3 的關係。
以下也呈現 G1 、 G2 與 G3 的三維散佈圖,我們可以從中發現 G1 、 G2 與 G3 之間有很強烈的線性關係。
若無法查看互動式三維散佈圖,或是需要全螢幕檢視,請點此處前往。
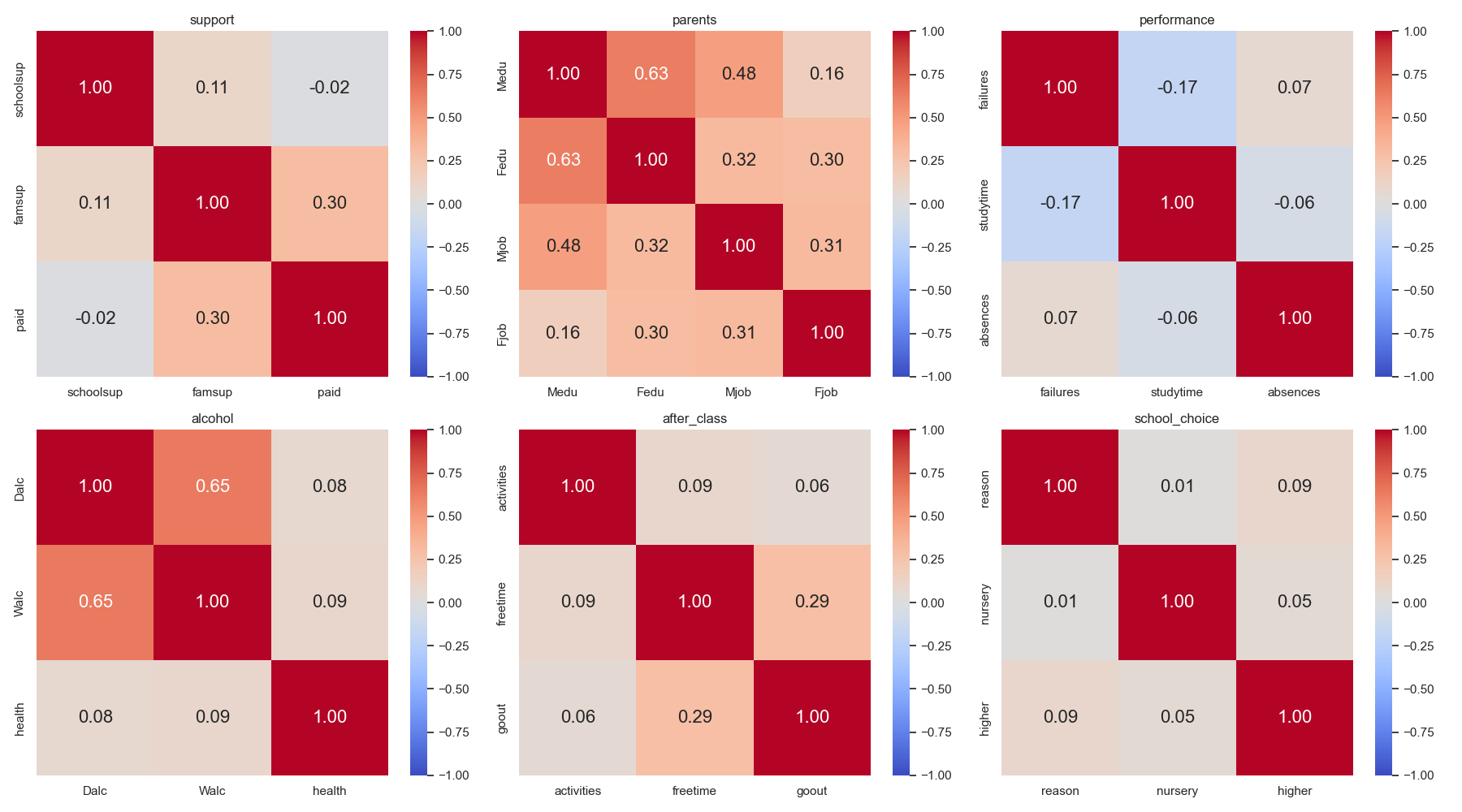
接下來呈現的是其他各組組內的相關係數圖。從以下的圖中,我們可以觀察到:
- 在
parents組內,父母間的教育程度與工作皆呈現高度正相關,這可以將parents組用於分析學生學習成績與其父母親是否有影響。 - 在
alcohol組內,我們發現平日飲酒與周末飲酒呈現高度的正相關,但與學生自己評估的健康狀態呈現幾乎無相關。 - 在
support組內,可以發現家庭給予學生的學業支持與額外的付費課程有正相關,這可能代表家庭會影響課外課程。 - 在
after_class組內,可以發現放學後的空閒時間和與朋友外出頻率有正相關,這可能代表學生放學後大多都會與朋友一起外出。
變數交互長條圖
以下挑選並繪製一些變數交互情形的長條圖,並觀察其資料呈現。
首先,繪製各年紀與其平均每週最少學習時間(studytime),因為已知
1表示每週少於 2 小時2表示每週 2 到 5 小時3表示每週 5 到 10 小時4表示每週至少 10 小時
因此,我們可以得知
1每週至少學習 0 小時2每週至少學習 2 小時3每週至少學習 5 小時4每週至少學習 10 小時
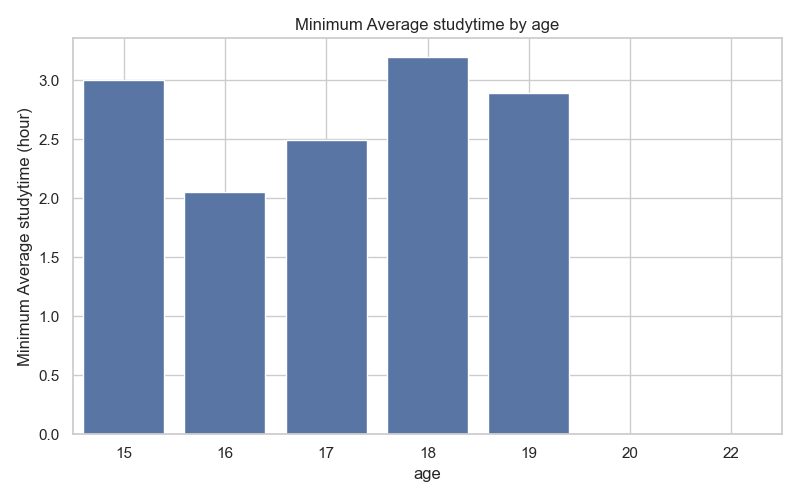
所以我們可以畫出以下各年紀與其平均每週最少學習時間長條圖。從圖中,我們可以發現 15 歲至 19 歲的學生每週平均至少會學習 2 至 3 小時,而 18 歲甚至每週至少學習 3 小時。我們推測 18 至 19 歲的學生可能因為有升學壓力,故每周學習時間較其他年齡段多;而 20 歲以上可能多為不喜歡學習或已有其他生涯打算的學生。
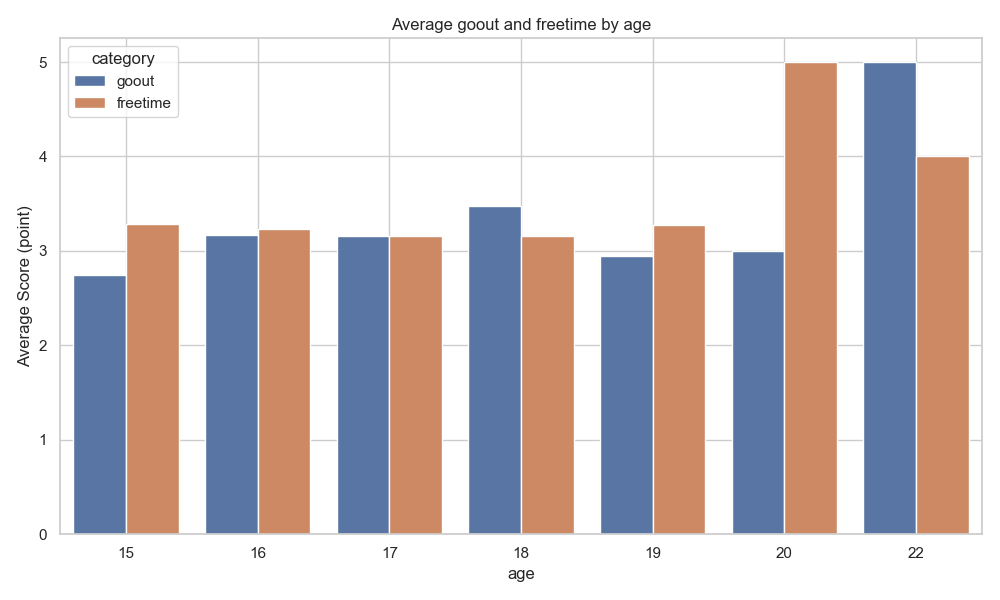
以下繪製放學後空閒時間(freetime)和與朋友外出頻率(goout)的長條圖,我們可以發現 15 歲至 19 歲的學生的放學後空閒時間和與朋友外出頻率平均皆為 3 點左右,而 20 歲以上的學生則較 15 歲至 19 歲的學生還高。與前一張圖進行比較,我們可以發現兩張圖的 20 歲以上的學生都與 15 歲至 19 歲的學生有許多不同之處,往後的分析可以多注意 age 這個變數產生的影響。
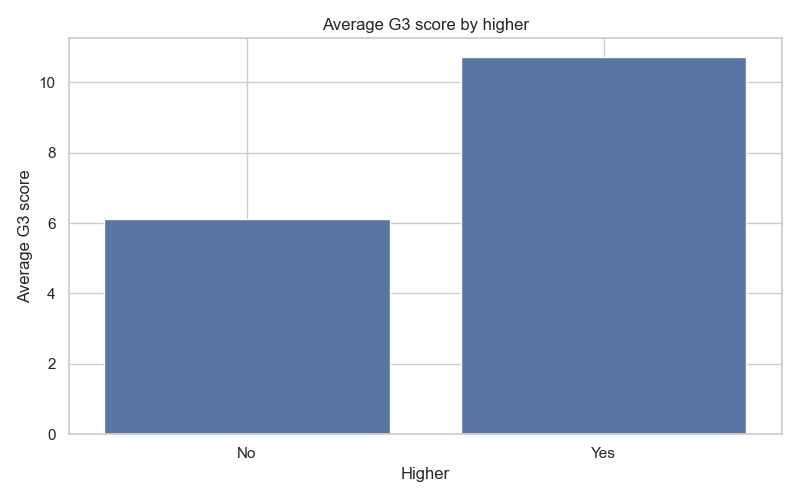
接下來繪製的是學生的升學意願(higher)與其平均 G3 成績長條圖。從此圖中,我們可以觀察到想進行升學的學生平均的 G3 成績較不想進行升學的學生高,顯示升學意願是影響學生學習成績的因素之一。
下面的這張圖是比較有意思的圖。根據葡萄牙的法律,成年年齡為 18 歲,購買與飲酒的合法年齡也同樣是 18 歲。在原始資料集的問卷中,飲酒行為的評分最低為 1 分,代表極少飲酒。因此如果學生完全不喝酒,多數分數應該要會集中在 1 。
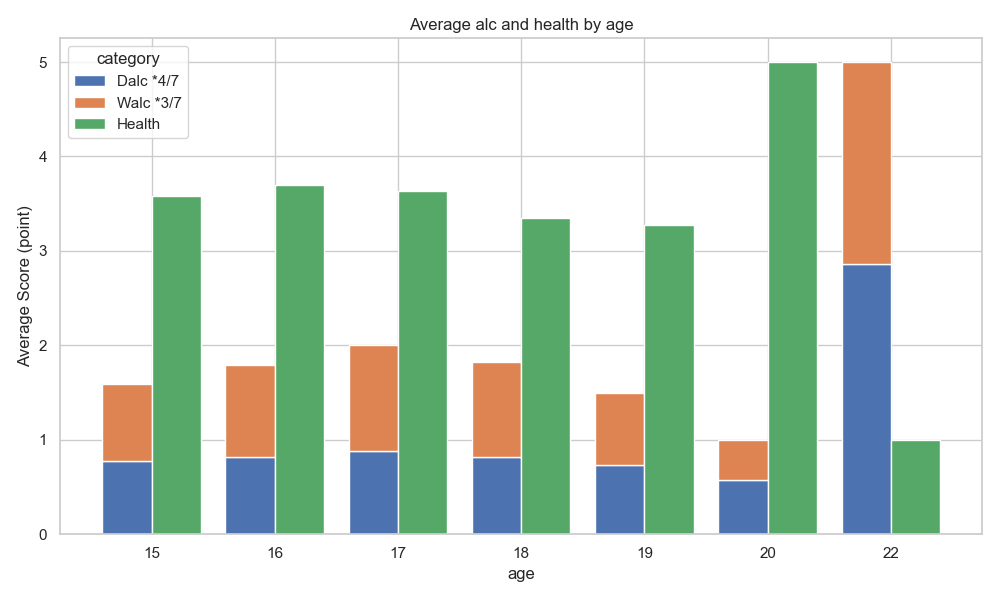
在下圖中的各年紀健康與平日、週末平均飲酒量長條圖中,我們繪製了學生自評的健康狀況與平日、週末平均飲酒量。其中,為了能直觀的以一週飲酒量與健康狀況進行比較,我們將平日、週末平均飲酒量疊在一起,且平日佔一週的 4 天,週末則佔了 3 天。這是因為學生大多在白天於學校學習,而飲酒的時間應該多在晚間,且許多人會把週五晚間視為週末,盡情玩樂放鬆。因此,此處將平日與週末各設為 4 天與 3 天。
我們同時可以看到部分 18 歲以下的學生平均飲酒量竟然會超過 1 點,這意味著這些學生中有一部分人實際上存在飲酒行為。
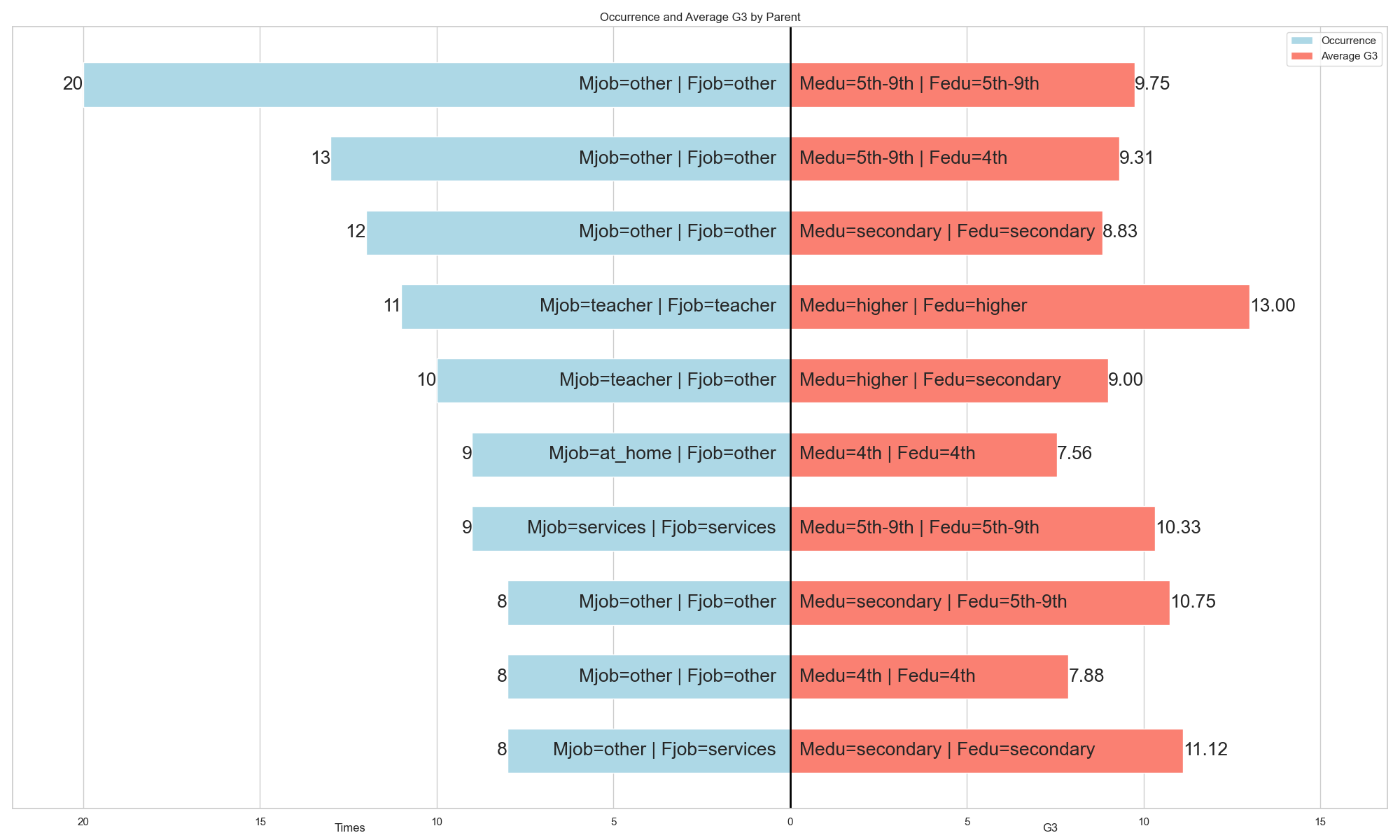
我們希望找出出現頻率最高的前 10 組由 Medu 、 Fedu 、 Mjob 、 Fjob 組成的組合,並計算每個組合對應的平均 G3 。
在下方的兩張圖中,左側的藍色長條顯示每個組合出現的次數,右側的紅色長條則顯示該組合的平均 G3 。
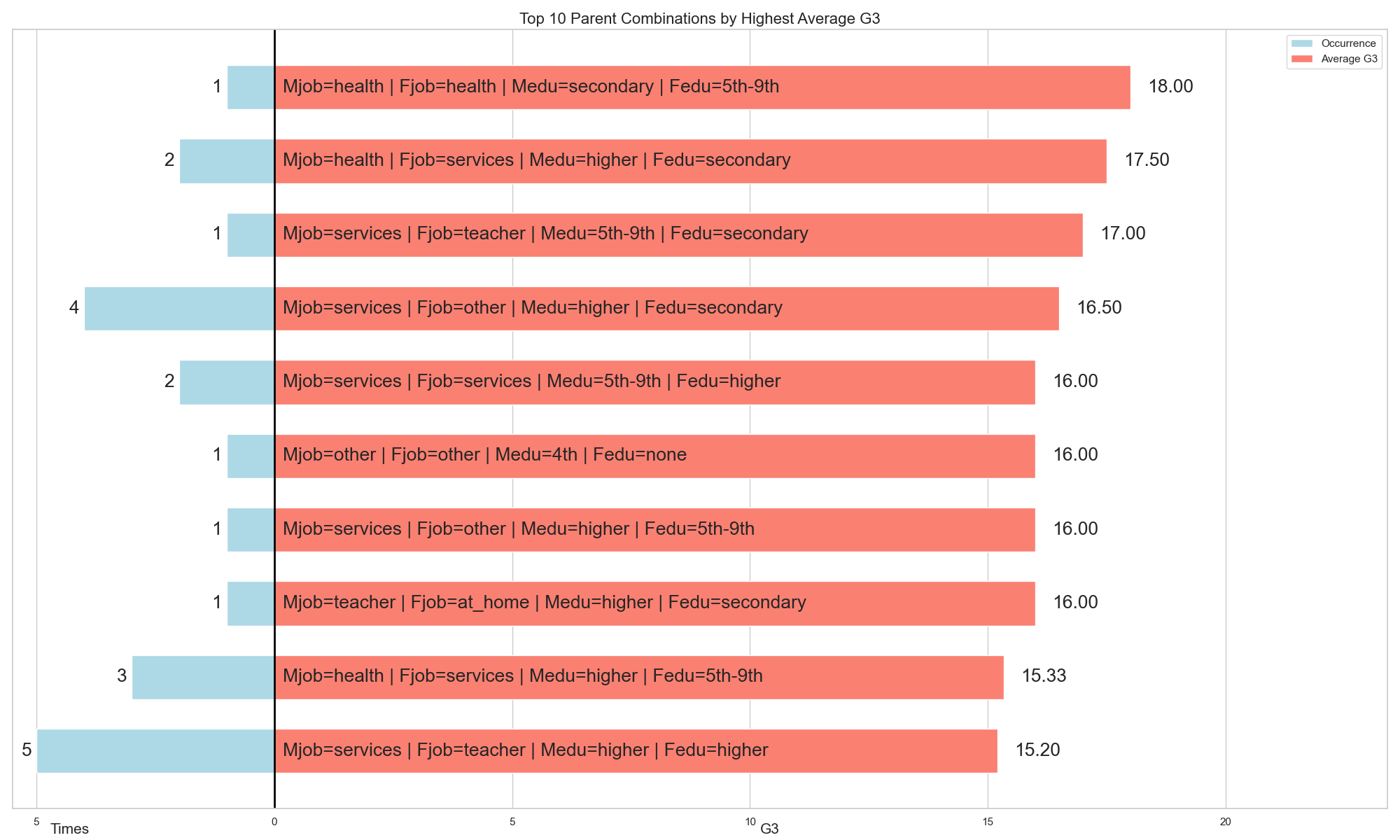
在計算出前 10 個最常出現的組合的平均 G3 之後,我們接著想找出平均 G3 最高的前 10 組合。
我們可以看到,當 Medu 和 Fedu 均為較高時,且 Mjob 和 Fjob 都是老師(teachers),學生的平均 G3 為 13.00;當 Fjob 為其他(other)時,平均 G3 為 9.00;而當 Mjob 為服務業(services)時,平均 G3 為 15.20。
因此我們可以看出,在相同的教育程度下,不同的 Mjob 和 Fjob 組合也會影響 G3 。
多維尺度分析
原始資料集中共有 33 個變數,且大多數變數之間的相關性相當低(接近於零),因此難以直接判斷哪些變數與 G3 成績相關。為了解決變數過多且解釋力分散的問題,我們首先依照先前對於變數的屬性與意義進行分組,再對每一組的變數套用多維尺度分析(MDS)以進行降維處理。
在 MDS 過程中,我們比較組內各筆學生資料的距離,將原本處於高維空間中的變數壓縮至二維,同時盡可能保留樣本間的相對關係,減少了變數數量,┼同時提升了各組對 G3 解釋能力。每組經過 MDS 降維後所產生的兩個新變數,會以該組名稱為前綴,並分別命名為 _dim1 與 _dim2。
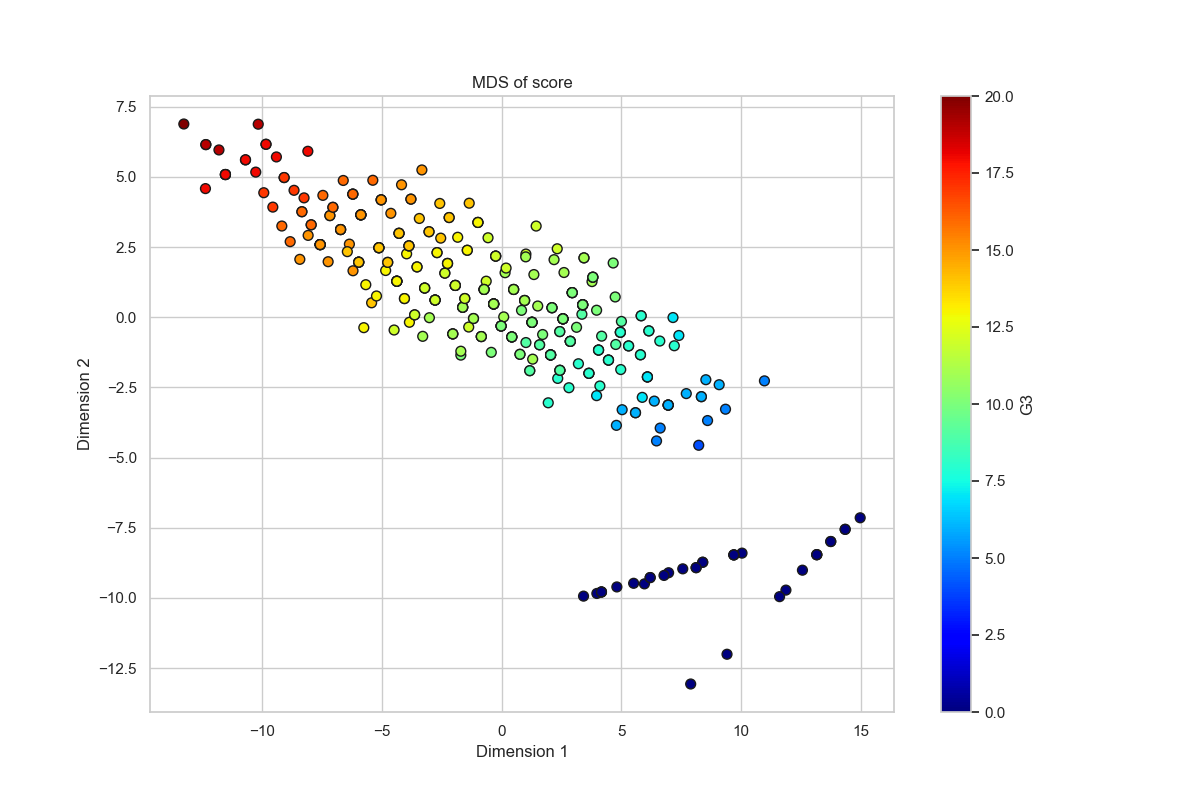
以下同時繪製各組經 MDS 降維後的結果,並同時將不同學生樣本以對應的 G3 成績上色,以視覺化呈現不同維度與學業表現之間的潛在關係。
雖然我們不分析 G1 、 G2 和 G3 ,但我們仍繪製出該變數經 MDS 降維後的樣本圖,可以與上面一起做比較。
經過 MDS 後,我們再繪製相關係數圖,用於查看降維後各變數間的關係。
若無法查看互動式相關係數圖,或是需要全螢幕檢視,請點此處前往。
成對圖
以下繪製成對圖,讓我們看看經過 MDS 後的變數有無較高的關聯性。
主成分分析
在進行主成分分析(PCA)前,我們先將變數進行標準化。將目標變數 G3 以外的變數進行標準化後會呈現如下形式:
| index | age | support_dim1 | support_dim2 | family_dim1 | family_dim2 | … | school_choice_dim1 | school_choice_dim2 | internet | romantic | sex_M |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.217015 | 1.087782 | -2.045391 | -0.911204 | -0.570128 | … | 0.238088 | -0.047286 | -2.38988 | -0.69196 | -0.952 |
| 1 | 0.393879 | -0.207043 | -0.836019 | 0.060769 | 1.546435 | … | 0.817325 | 0.615202 | 0.41843 | -0.69196 | -0.952 |
| 2 | -1.25239 | -2.043003 | -0.695022 | 0.514605 | 0.288704 | … | -1.813855 | 1.842271 | 0.41843 | -0.69196 | -0.952 |
| 3 | -1.25239 | -0.697640 | 1.009037 | 0.877950 | -0.557109 | … | -0.814591 | 0.867946 | 0.41843 | 1.44516 | -0.952 |
| 4 | -0.42925 | -0.697640 | 1.009037 | 0.700091 | 0.735734 | … | -0.814591 | 0.867946 | -2.38988 | -0.69196 | -0.952 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 344 | 1.217015 | -0.207043 | -0.836019 | 0.027745 | 0.240671 | … | 0.238088 | -0.047286 | 0.41843 | -0.69196 | -0.952 |
| 345 | 1.217015 | 1.386098 | -0.426182 | -0.600978 | 0.964057 | … | -1.803388 | 1.853657 | 0.41843 | 1.44516 | -0.952 |
| 346 | 1.217015 | 1.386098 | -0.426182 | -1.135662 | 0.929772 | … | 0.238088 | -0.047286 | 0.41843 | 1.44516 | 1.049 |
| 347 | 1.217015 | -0.697640 | 1.009037 | -0.600978 | 0.964057 | … | 0.238088 | -0.047286 | 0.41843 | 1.44516 | 1.049 |
| 348 | 0.393879 | -0.697640 | 1.009037 | 0.027745 | 0.240671 | … | 1.254272 | -1.000397 | 0.41843 | 1.44516 | -0.952 |
以下顯示經過 PCA 處理後各主成分的權重(loadings),並且同時寫出每一個主成分的解釋變異量(Explained Variance)、重要變數(Most Important Feature)以及累積解釋變異量(Cumulative Explained Variance)。
其中,重要變數的選擇是每一個主成分中的 loadings 取絕對值後最大的一個變數。
| age | support_dim1 | support_dim2 | family_dim1 | family_dim2 | parents_dim1 | parents_dim2 | performance_dim1 | performance_dim2 | alcohol_dim1 | … | after_class_dim1 | after_class_dim2 | school_choice_dim1 | school_choice_dim2 | internet | romantic | sex_M | Explained Variance | Cumulative Explained Variance | Most Important Feature | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | -0.31428 | -0.01492 | -0.09142 | 0.02471 | 0.07027 | 0.00225 | -0.01428 | 0.56291 | 0.56998 | -0.13261 | … | 0.12635 | 0.18285 | 0.12075 | -0.14428 | -0.12218 | -0.24775 | 0.05817 | 0.123739 | 0.123739 | performance_dim2 |
| PC2 | 0.05854 | -0.15301 | -0.05277 | -0.01508 | -0.08101 | 0.11834 | 0.12734 | -0.20177 | -0.15329 | -0.33308 | … | 0.27279 | -0.08147 | 0.55584 | -0.46000 | -0.06047 | 0.01056 | -0.35919 | 0.104542 | 0.228281 | school_choice_dim1 |
| PC3 | -0.25162 | -0.33288 | 0.12403 | 0.25912 | 0.04080 | -0.21617 | -0.19674 | -0.10099 | -0.08990 | -0.25778 | … | 0.42266 | 0.06376 | -0.24370 | 0.41533 | 0.16350 | 0.03533 | -0.27323 | 0.089062 | 0.317343 | after_class_dim1 |
| PC4 | 0.18089 | 0.23004 | -0.21277 | -0.12089 | -0.06424 | 0.55154 | 0.12192 | 0.08621 | 0.02896 | -0.15634 | … | 0.18814 | -0.14339 | -0.29892 | 0.29881 | -0.42365 | 0.07793 | -0.25812 | 0.082954 | 0.400297 | parents_dim1 |
| PC5 | 0.09728 | 0.23079 | -0.27532 | -0.35041 | 0.51664 | -0.11613 | -0.15667 | -0.16518 | -0.18069 | -0.06037 | … | 0.03337 | 0.38923 | 0.02474 | 0.00286 | 0.01517 | 0.10256 | 0.14521 | 0.076042 | 0.476339 | family_dim2 |
| PC6 | 0.16847 | -0.20377 | 0.52457 | -0.37602 | 0.41667 | 0.08991 | 0.33865 | 0.10907 | 0.18200 | -0.12810 | … | -0.16270 | -0.13117 | -0.06696 | 0.05962 | 0.24155 | 0.02600 | -0.20855 | 0.066698 | 0.543037 | support_dim2 |
| PC7 | -0.13403 | 0.16553 | 0.03740 | 0.34388 | -0.02806 | 0.25739 | 0.60921 | -0.03758 | -0.04892 | -0.08187 | … | 0.13169 | 0.40514 | -0.01908 | 0.00350 | 0.28333 | 0.25359 | 0.24462 | 0.060366 | 0.603402 | parents_dim2 |
| PC8 | 0.37215 | 0.32579 | 0.02033 | 0.26236 | 0.03516 | -0.07732 | -0.35951 | 0.23284 | 0.23434 | -0.24334 | … | -0.00137 | -0.07107 | 0.03513 | -0.09724 | 0.27742 | 0.51081 | -0.13665 | 0.058127 | 0.661529 | romantic |
| PC9 | -0.04030 | -0.39534 | 0.04481 | -0.07430 | -0.22586 | 0.09811 | -0.06035 | 0.07540 | 0.07128 | 0.42277 | … | -0.20239 | 0.26401 | 0.05025 | -0.02830 | -0.17433 | 0.56876 | -0.17478 | 0.054081 | 0.715610 | romantic |
| PC10 | 0.32727 | 0.17252 | 0.61629 | 0.01171 | -0.15288 | -0.13744 | -0.04751 | 0.01093 | -0.02539 | 0.12011 | … | 0.40903 | 0.11550 | 0.07008 | -0.01209 | -0.35258 | -0.04926 | 0.29073 | 0.049724 | 0.765334 | support_dim2 |
| PC11 | 0.22969 | -0.26312 | -0.00117 | -0.06563 | -0.09572 | -0.07595 | -0.05341 | -0.03554 | 0.03893 | -0.45823 | … | -0.19930 | 0.58174 | -0.09997 | 0.01158 | -0.27012 | -0.07807 | -0.03096 | 0.046235 | 0.811570 | after_class_dim2 |
| PC12 | 0.25752 | -0.17788 | 0.00275 | 0.60756 | 0.52036 | 0.23676 | -0.08113 | -0.06917 | 0.01976 | 0.27676 | … | -0.08760 | 0.07145 | 0.02855 | -0.07412 | -0.17312 | -0.23242 | -0.12077 | 0.041150 | 0.852720 | family_dim1 |
| PC13 | 0.18436 | 0.12262 | 0.09962 | -0.08477 | -0.35041 | 0.33747 | -0.24372 | 0.01910 | -0.05377 | 0.13521 | … | -0.07200 | 0.31544 | -0.03596 | -0.00568 | 0.48422 | -0.43045 | -0.22621 | 0.035231 | 0.887951 | internet |
| PC14 | -0.23559 | -0.18653 | 0.09688 | -0.21986 | 0.19514 | 0.50116 | -0.39481 | -0.01050 | -0.01521 | 0.05864 | … | 0.36308 | 0.02747 | 0.04392 | -0.10603 | 0.10683 | 0.14587 | 0.26635 | 0.034410 | 0.922361 | parents_dim1 |
| PC15 | 0.51158 | -0.48800 | -0.35236 | -0.03468 | -0.11947 | -0.00802 | 0.11331 | 0.09324 | 0.08548 | -0.02816 | … | 0.20338 | -0.17840 | -0.11567 | -0.01638 | 0.21865 | -0.03666 | 0.41258 | 0.032990 | 0.955352 | age |
| PC16 | 0.12207 | 0.07406 | -0.20073 | -0.16652 | 0.07581 | -0.29201 | 0.21268 | 0.08410 | 0.09351 | 0.42624 | … | 0.46395 | 0.18854 | -0.14068 | -0.13191 | 0.07381 | -0.02104 | -0.39930 | 0.024505 | 0.979856 | after_class_dim1 |
| PC17 | 0.11616 | -0.00761 | -0.09411 | -0.03805 | 0.02841 | -0.00119 | 0.03888 | 0.17998 | -0.03532 | 0.09370 | … | 0.02228 | 0.05660 | 0.67791 | 0.66363 | 0.04566 | -0.01960 | -0.00163 | 0.013824 | 0.993680 | school_choice_dim1 |
| PC18 | 0.00832 | 0.06218 | -0.03136 | -0.03381 | -0.06435 | 0.02330 | -0.01424 | -0.68519 | 0.70113 | 0.04366 | … | 0.02955 | 0.00129 | 0.08253 | 0.12981 | 0.02290 | -0.00060 | 0.02883 | 0.006320 | 1.000000 | performance_dim2 |
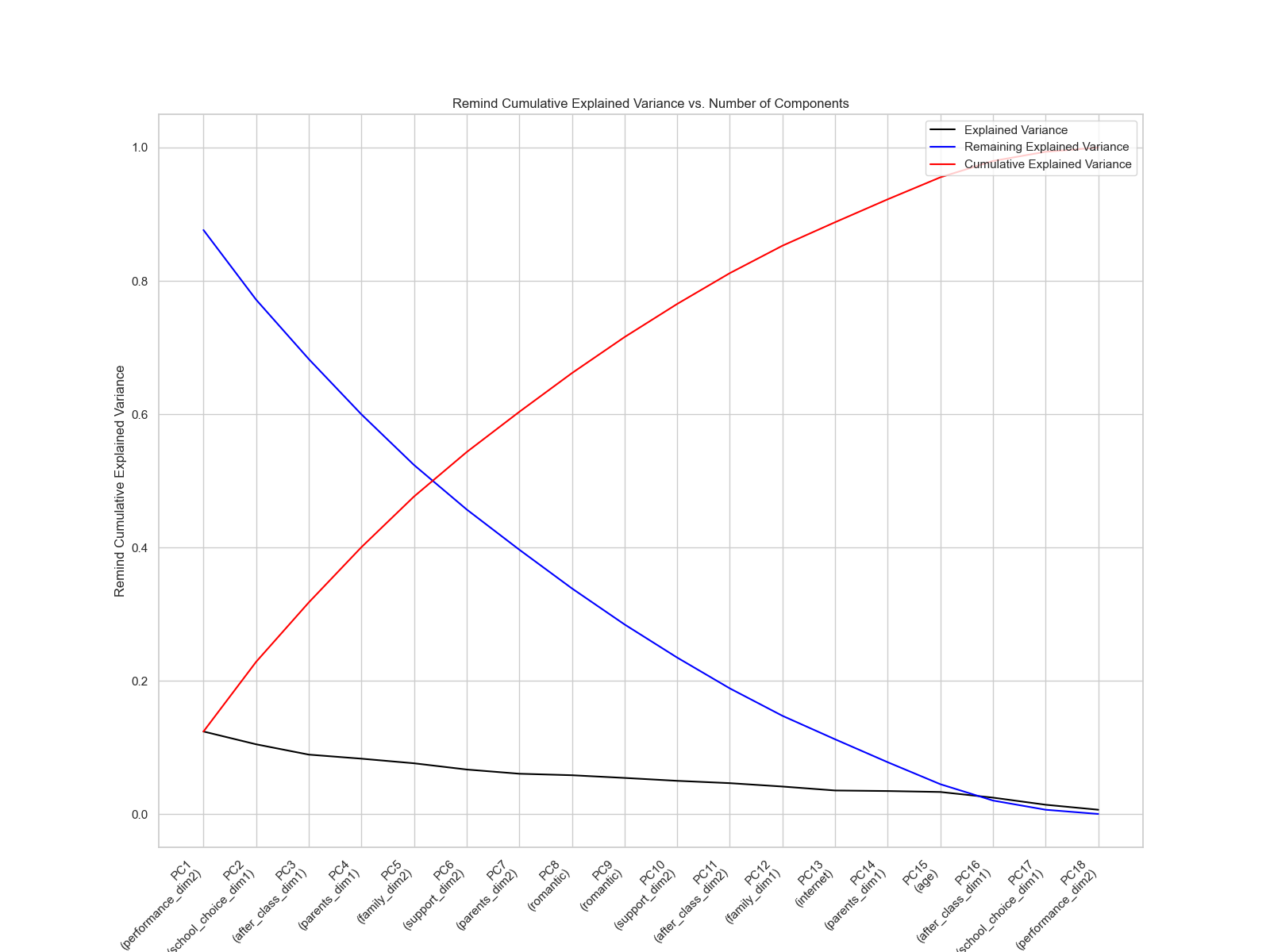
繪製變異數圖可以協助我們更好地分析這一筆資料。其中黑線表示各成分的解釋變異量,藍線表示剩餘的解釋變異量,紅線則表示累積的解釋變異量。
當然,我們也可以將經過 PCA 轉換後的所有變數算出來,呈現如下。
| Index | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | … | PC15 | PC16 | PC17 | PC18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -5.510839 | 1.127293 | -4.117657 | 3.107669 | 2.864756 | 1.596422 | -5.251726 | … | 9.138033 | 0.807222 | 1.855121 | 0.349057 |
| 1 | -3.477549 | 1.540630 | -4.339357 | 4.639965 | 1.925990 | 4.441370 | -1.301991 | … | 9.372359 | 0.938431 | 2.687517 | 0.665990 |
| 2 | -7.996224 | 0.857119 | -2.236678 | 4.270145 | 1.455193 | 2.076697 | -0.357673 | … | 8.280973 | 1.682065 | 2.160862 | -3.14570 |
| 3 | -1.713179 | -0.138464 | -1.645506 | 2.585313 | 0.984078 | 2.730721 | -2.543466 | … | 8.935648 | 2.044699 | 1.432726 | 2.032150 |
| 4 | -3.250539 | 0.438469 | -3.461779 | 4.108225 | 1.205912 | 4.030496 | -0.474944 | … | 8.956492 | 2.556946 | 1.910259 | 0.608520 |
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| 344 | -4.299600 | 1.316663 | -4.763758 | 3.739167 | 1.177631 | 4.059481 | -1.511099 | … | 10.022404 | 2.260172 | 2.207069 | 1.525158 |
| 345 | -7.601288 | -0.275631 | -3.954244 | 4.220185 | 2.496979 | 3.148704 | -2.224165 | … | 8.215032 | 1.755102 | 2.104987 | 0.928338 |
| 346 | -8.095515 | 1.264441 | -3.196450 | 1.115171 | 4.848870 | 1.962490 | -3.098767 | … | 9.138925 | 2.697971 | 1.810029 | 0.542200 |
| 347 | -1.969261 | -1.791564 | -6.257189 | 0.902714 | 0.909935 | 5.697392 | -2.812854 | … | 10.234261 | 3.180343 | 2.534447 | 2.330287 |
| 348 | -1.054689 | 0.131606 | -5.522433 | 1.743504 | 0.374565 | 5.017756 | -1.248375 | … | 9.365234 | 3.594221 | 2.535474 | 2.333115 |
以下繪製 PC1 、 PC2 以及 PC3 累積變異量的每個變數的三維權重散佈圖。
若無法查看 PC1 vs. PC2 vs. PC3 權重散佈圖,或是需要全螢幕檢視,請點此處前往。
迴歸模型
Python 有許多模組都提供計算迴歸模型的工具,如 sklearn 和 statsmodels 等模組。其中
sklearn偏向機器學習設計,強調預測與泛化能力,但許多統計指標都需要自行使用程式碼撰寫。statsmodels偏向統計建模與推論,更適合做學術或統計分析,並提供簡單的模型摘要(summary)。
以下使用 statsmodels 模組進行分析與繪圖。
原始資料集
這裡先對整理後的原始資料進行迴歸,我們可以發現:
- 原始資料的 $R^2$ 為 0.269 ,這表示此迴歸模型的解釋力偏低。且 Adj. $R^2$ 更低,表示部分變數可能是冗餘的。
- P-value = $1.80 \times 10^{-9}$,這表示有變數對
G3有顯著影響。failures的 P-value 是 0.000,且其係數為負,這表示failures對G3有顯著負面影響,失敗次數越多,成績越差。goout的 P-value 是 0.001,且其係數為負,這表示外出頻率對G3有顯著負面影響。schoolsup的 P-value 是 0.000,且其係數為負,這表示接受學校額外支援者成績較差,可能因學習困難需要支援。romantic的 P-value 是 0.019,且其係數為負,這表示戀愛經驗對G3有顯著負面影響。sex_M的 P-value 是 0.015,且其係數為正,這表示男性的成績顯著高於女性。address_0的 P-value 是 0.005,且其係數為正,這表示住在都市區的學生成績較高。famsize_1的 P-value 是 0.004,且其係數為正,這表示大家庭學生的成績顯著較好。Pstatus_1的 P-value 是 0.020,且其係數為正,這表示父母分居的學生成績顯著較高。Mjob_2(母親為醫療人員)的 P-value 是 0.047,且其係數為正,這表示此職業對子女成績有正向影響。Mjob_3(母親為公務員)的 P-value 是 0.012,且其係數為正,這表示此職業對子女成績有顯著正面影響。
| |
經 MDS 轉換後的資料集
- P-value = $4.23 \times 10^{-8}$,表示此模型整體對
G3的預測是顯著的。age的 P-value 是 0.011,且係數為負,表示年齡越大,成績可能愈差。support_dim1的 P-value 是 0.009,且係數為正,表示支援相關特徵(如學校支援、家庭支援)第一維與G3有顯著正向關聯。support_dim2的 P-value 是 0.005,且係數為正,表示支援第二維亦有顯著正向影響。family_dim2的 P-value 是 0.009,且係數為正,表示家庭相關因素的第二維度與G3有顯著正向關聯。parents_dim1的 P-value 是 0.046,且係數為負,表示某些父母背景因素可能對G3有顯著負面影響。performance_dim1的 P-value 是 0.030,且係數為負,可能表示某些學業表現背景對G3有負面關聯。after_class_dim1的 P-value 是 0.014,且係數為正,表示課後活動第一維度對G3有顯著正面影響。after_class_dim2的 P-value 是 0.034,且係數為正,表示課後活動第二維度也有顯著正向影響。romantic的 P-value 是 0.008,且係數為負,表示有戀愛關係對G3有顯著負面影響。
| |
經 MDS 和 PCA 轉換後的資料集
以下將所有資料點經 PCA 轉換後,再進行迴歸。由迴歸模型,我們可以發現:
- PCA 轉換後的資料點所進行的 MSE 與前一個模型相同。
- 使用各成分進行迴歸,可以發現 PC1 、 PC4 、 PC9 、 PC10 、 PC15 對
G3有較顯著影響。
從先前對各主成分中重要變數的分析,我們可以發現對此模型有影響的變數是
| PC1 | PC4 | PC9 | PC10 | PC15 | |
|---|---|---|---|---|---|
| 重要變數 | performance_dim2 | parents_dim1 | romantic | support_dim2 | age |
| 影響 | + | - | - | + | - |
| |
經 MDS 和 PCA 轉換後選取 80% 變異量的資料集
以下使用 PCA 前 80% 解釋變異量的 PC 進行迴歸分析,我們可以發現:
- 前 80% 解釋變異量的 PC 轉換後的資料點的 $R^2$ 為 0.137 ,相比於原始資料的模型解釋力下降。
- 使用各成分進行迴歸,可以發現 PC1 、 PC4 、 PC5 、 PC9 對
G3有較顯著影響。
| PC1 | PC4 | PC5 | PC9 | |
|---|---|---|---|---|
| 重要變數 | performance_dim2 | family_dim2 | romantic | |
| 影響 | + | - | + | + |
由於此資料集仍能夠完整送入迴歸模型進行建模,因此我們不需要使用 PCA 方法進行降維後再建模,因為這反而會降低模型對資料集的解釋力、增加平均平方誤差。
| |
QQ plots
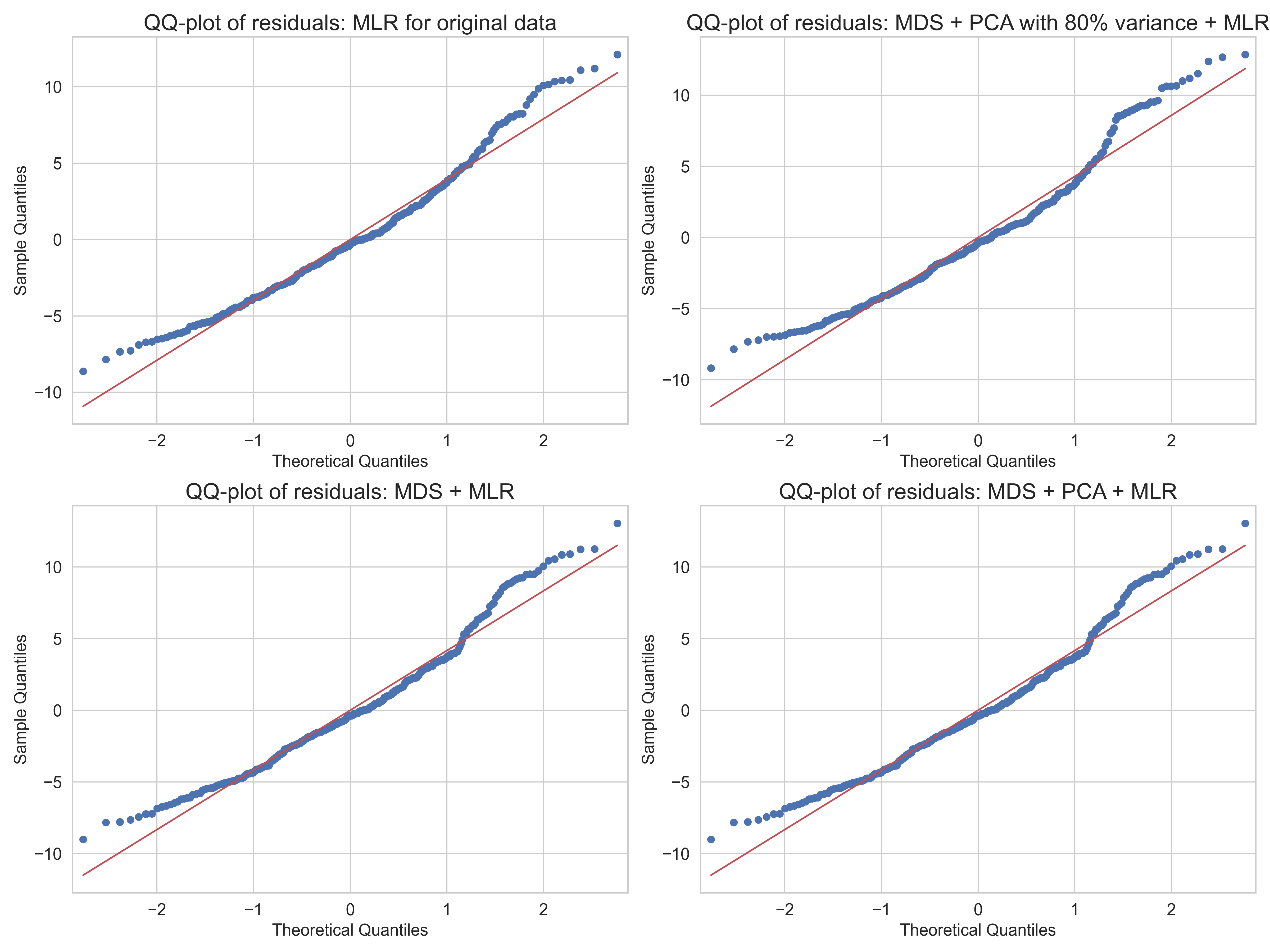
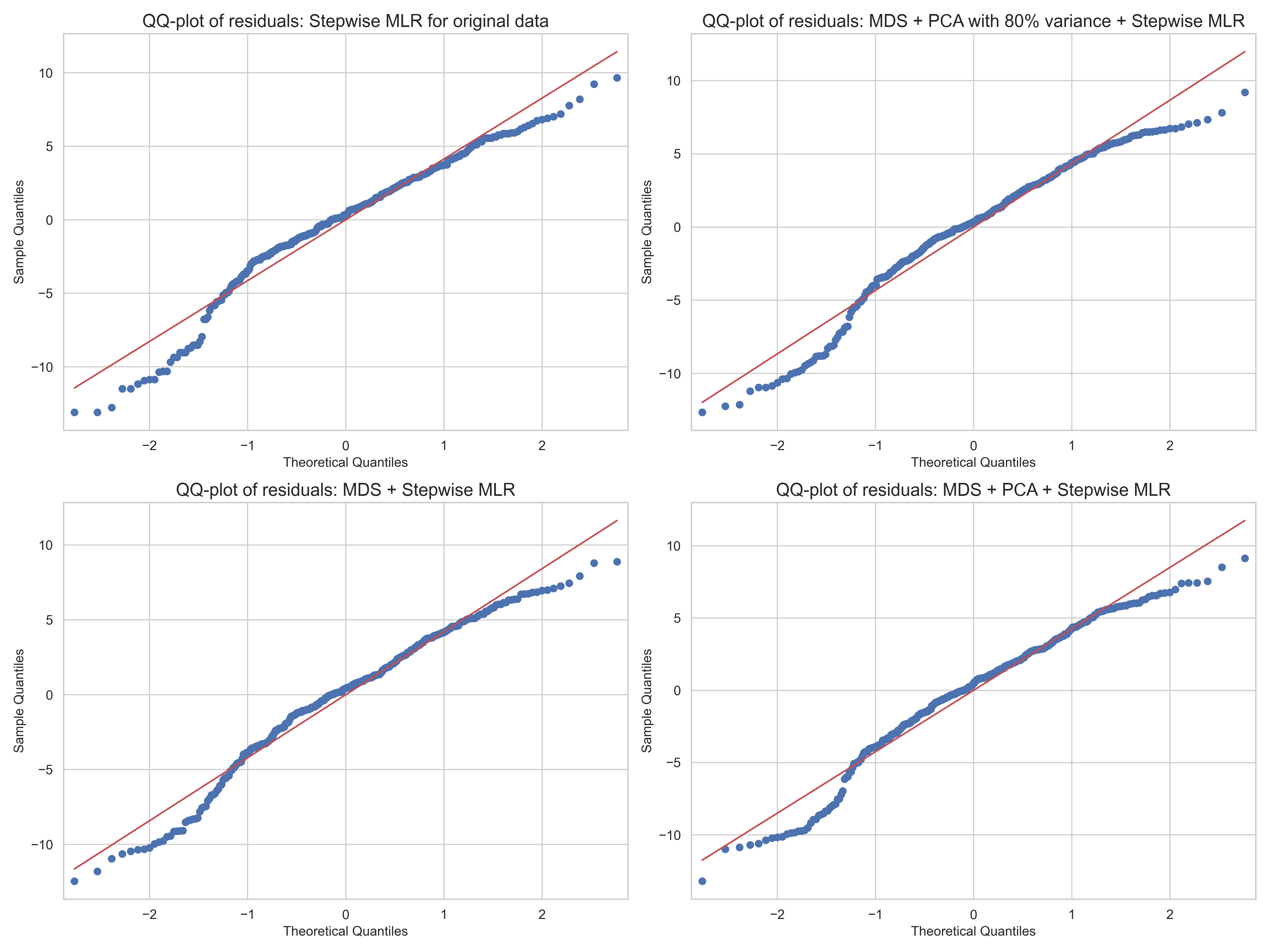
以下繪製上述四模型的 QQ plots 。根據下圖四種模型的 QQ-plot,可觀察殘差是否近似常態分布:
- 原始資料(有刪除
MS和G1、G2) + 迴歸:整體擬合最佳,但右尾偏離明顯,表示存在極端高分預測誤差。 - MDS + 迴歸:模型簡單,但殘差尾部有較大偏差,表示極端值影響較大。
- MDS + PCA + 迴歸:尾部偏離略有改善,但中尾仍未貼近理想直線,殘差分布仍不理想。
- MDS + PCA (80% 解釋變異量) + 迴歸:偏離常態較明顯,特別在右尾,可能是 PCA 資訊壓縮過多。
四種模型皆未完全滿足殘差常態性假設,但以原始資料集的表現最接近常態。
逐步挑選變數
還記得我們的目標嗎?我們想要找出究竟有那些變數會影響 G3 。因此,在這裡我們打算將變數逐步放入迴歸模型中,並建立模型,以逐步查看加入該變數是否能有效提升迴歸模型對於 G3 的擬合能力。
這聽起來很熟悉嗎?沒錯,這裡打算使用類似於 R 語言中的 step() 函數進行實作,以下將會實作出 Bidirectional elimination (雙向淘汰)的逐步迴歸分析函數(stepwise regression),並用於挑選變數。
| |
逐步迴歸包含三個部分:
前向逐步: 在初始設定中,迴歸模型中沒有變數。因此,我們隨後逐步加入變數,然後將這些選定的變數組合成預測變數。
後向消除: 我們在初始步驟中列出所有預測變數。然後,逐一消除變數,檢查模型是否成立。
雙向消除: 它像前向逐步一樣添加預測變數,但也會剔除任何在此過程中變得無關緊要的變數。
透過設定 p-value$ = 0.05$ 的門檻值並逐步挑選完變數,我們可以得到以下結果:
| 方法 | 選擇變數 |
|---|---|
原始資料(有刪除 MS 和 G1 、 G2) + 迴歸 | failures, goout, Mjob_1, Mjob_0, sex_M |
| MDS + 迴歸 | parents_dim1, after_class_dim1, family_dim2, romantic, support_dim2, after_class_dim2, support_dim1, age, performance_dim1, const |
| MDS + PCA + 迴歸 | PC9, PC1, PC15, PC10, PC8, PC18 |
| MDS + PCA (80% 解釋變異量) + 迴歸 | PC4, PC9, PC1, PC8, PC10 |
再次 PCA
此處使用經過 MDS 且挑選過的變數再次進行 PCA ,結果如下:
| PC | parents_dim1 | after_class_dim1 | family_dim2 | romantic | support_dim2 | after_class_dim2 | support_dim1 | age | performance_dim1 | const | Explained Variance | Cumulative Explained Variance | Most Important Feature |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | 0.213121 | -0.205577 | -0.060527 | 0.434094 | 0.056771 | -0.286477 | 0.223825 | 0.623287 | -0.443102 | 0.0 | 0.166152 | 0.166152 | age |
| PC2 | 0.448179 | -0.083659 | 0.074404 | -0.061783 | -0.540231 | 0.133070 | 0.588515 | 0.021220 | 0.355564 | 0.0 | 0.143947 | 0.310098 | support_dim1 |
| PC3 | -0.406978 | -0.415160 | 0.623954 | 0.116911 | 0.022111 | 0.475853 | 0.128447 | 0.110293 | -0.058623 | -0.0 | 0.129111 | 0.439210 | family_dim2 |
| PC4 | 0.081492 | 0.512700 | -0.044706 | 0.497163 | -0.318840 | 0.496922 | -0.143583 | -0.122033 | -0.311816 | -0.0 | 0.113825 | 0.553034 | after_class_dim1 |
| PC5 | 0.258220 | 0.589895 | 0.613767 | -0.218113 | 0.319698 | -0.105588 | 0.107590 | 0.189307 | -0.017143 | -0.0 | 0.104848 | 0.657882 | family_dim2 |
| PC6 | 0.248523 | -0.047805 | -0.180789 | 0.402815 | 0.601967 | 0.323911 | 0.032664 | 0.052785 | 0.519491 | 0.0 | 0.100250 | 0.758132 | support_dim2 |
| PC7 | -0.600307 | 0.359132 | -0.276512 | 0.029457 | 0.122379 | -0.030260 | 0.643747 | 0.043791 | 0.033295 | -0.0 | 0.091065 | 0.849197 | support_dim1 |
| PC8 | -0.128970 | 0.015051 | 0.337069 | 0.578870 | -0.116411 | -0.555072 | -0.001069 | -0.386453 | 0.251855 | 0.0 | 0.083395 | 0.932592 | romantic |
| PC9 | -0.275680 | 0.189882 | -0.003829 | 0.033395 | -0.331180 | -0.042056 | -0.373340 | 0.627789 | 0.491798 | 0.0 | 0.067408 | 1.000000 | age |
| PC10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.0 | 0.000000 | 1.000000 | const |
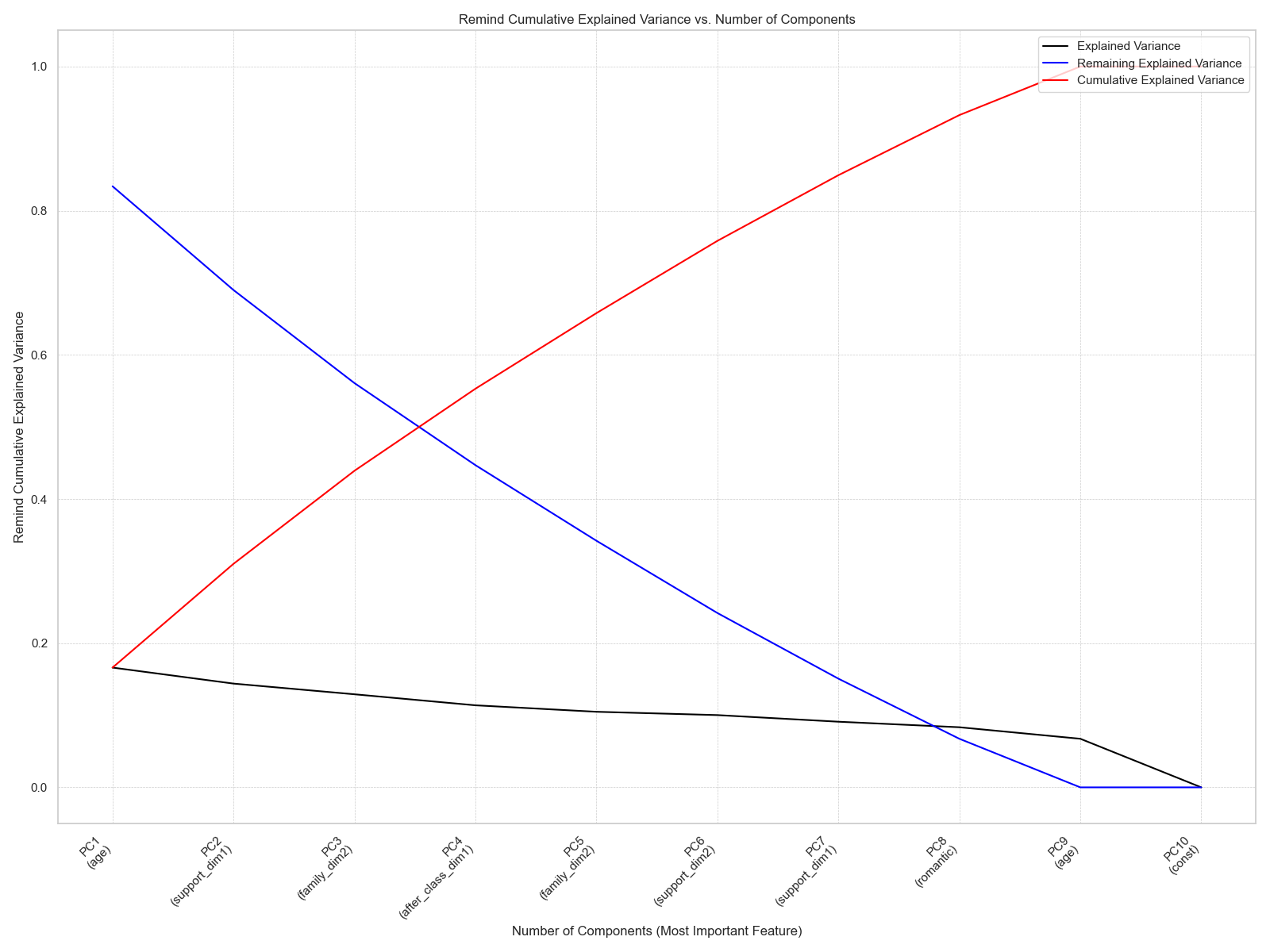
從以上表格可能無法很好看出各變數之間的關係。因此,這裡再次繪製經變數挑選後進行主成分分析的變異數圖。可以發現至少要選取到 PC7 ,才能夠解釋超過 80% 的累積變異量。
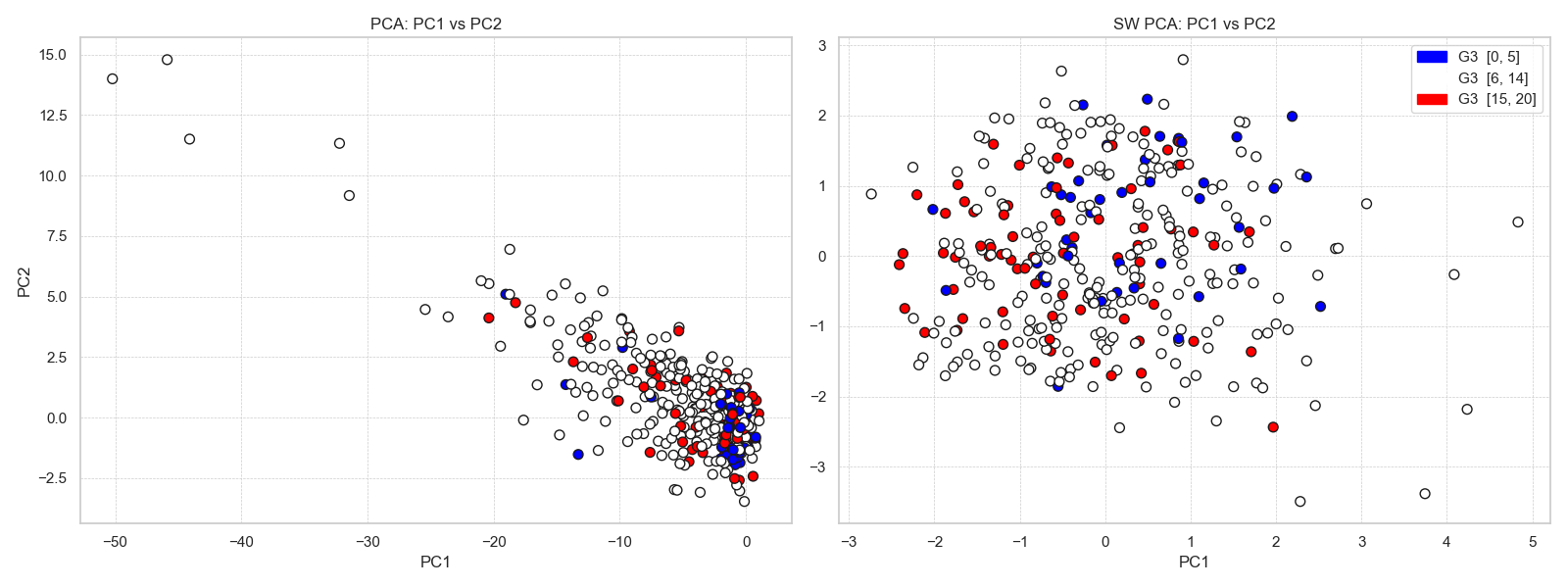
以下繪製原資料集與經變數挑選後的 PC1 與 PC2 樣本散佈圖,並以 G3 作為上色標準。其中,為了能有效看出高分群與低分群的差異,這裡將 G3 中 15 分至 20 分作為高分區,並以紅色表示; 0 至 5 分作為低分區,並以藍色表示。
在上圖中,左圖為原整理後的資料集進行 PCA 後的結果,右圖為挑選變數後的 PCA(SW PCA)。
PCA:PC1 vs. PC2
- 高分、中分與低分樣本在平面上混雜分布,無明顯的群聚或分界。
- 雖然 PC1 和 PC2 捕捉了最多的總變異量,但它們未必與
G3直接相關。 - 這顯示對全體原始變數進行 PCA 時,前兩個主成分對
G3並沒有強烈的區分能力。
SW PCA:PC1 vs. PC2
- 高分群主要集中在PC1 為正值的區域。
- 低分群則集中在PC1 為負值的區域。
這表示在變數選擇後再進行 PCA,能讓主成分(特別是 PC1)更有效地區分不同分數層級。
QQ plots
經過以上變數挑選後,進行迴歸分析的 QQ plots 如下:
模型比較
已知經過 PCA 後但只取前 n% 變異量所含的資訊,一定比完整 PCA 還損失更多資訊。因此,此處暫不討論。
以下比較上述所提出的六個模型。
| 模型 | $R^2$ | Adj. $R^2$ | MSE | P-value | AIC |
|---|---|---|---|---|---|
原始資料(有刪除 MS 和 G1 、 G2) + 迴歸 | 0.268987 | 0.194960 | 62.583249 | 0.915722 | 2015.098094 |
| MDS + 迴歸 | 0.187554 | 0.143239 | 77.576792 | 0.749395 | 2023.958578 |
| MDS + PCA + 迴歸 | 0.187554 | 0.143239 | 77.576792 | 0.614297 | 2023.958578 |
原始資料(有刪除 MS 和 G1 、 G2) + 逐步迴歸 | 0.197138 | 0.185435 | 293.547188 | 0.036654 | 1993.817204 |
| MDS + 逐步迴歸 | 0.169384 | 0.147332 | 140.122389 | 0.020078 | 2013.677881 |
| MDS + PCA + 逐步迴歸 | 0.169384 | 0.147332 | 140.122389 | 0.511294 | 2013.677881 |
由上表,我們可以發現使用原始資料(有刪除 MS 和 G1 、 G2) + 迴歸的模型,對於 G3 能有較好的擬合能力,使得模型解釋能力 $R^2$ 和 Adj. $R^2$ 是所有模型中最高的,且平均平方誤差最低,代表模型能較好地解釋資料變異並具備較小的預測誤差。另一方面,我們也可以發現原始資料(有刪除 MS 和 G1 、 G2) + 逐步迴歸和 MDS + PCA + 逐步迴歸的模型擁有相對較低的 P-value ,顯示這些模型中的變數對 G3 有統計上顯著的影響。這意味著這些模型能挑選出對應變數具高解釋力的自變數。進一步比較 AIC 值,原始資料(有刪除 MS 和 G1 、 G2) + 逐步迴歸模型的 AIC 最低,代表該模型在考量解釋力與模型複雜度後,整體表現最為理想。
以下顯示各模型具有影響力的前三大變數。
| 模型 | Top1 | Top2 | Top3 |
|---|---|---|---|
原始資料(有刪除 MS 和 G1 、 G2) + 迴歸 | failures | schoolsup | paid |
| MDS + 迴歸 | romantic | support_dim2 | support_dim1 |
| MDS + PCA + 迴歸 | PC9 | PC10 | PC15 |
原始資料(有刪除 MS 和 G1 、 G2) + 逐步迴歸 | Mjob_1 | failures | Mjob_0 |
| MDS + 逐步迴歸 | romantic | support_dim2 | support_dim1 |
| MDS + PCA + 逐步迴歸 | PC9 | PC7 | PC5 |
綜上所述,這裡選取原始資料(有刪除 MS 和 G1 、 G2) + 逐步迴歸模型作為評判 G3 的模型。從此模型,我們可以知道影響學生的變數為母親的工作與課程失敗次數,顯示家庭與學生在學校課程的表現是動搖最終成績的關鍵。
結語
透過此次的合作資料分析,我們學習到了許多過去未曾接觸過的分析方法。透過腦力激盪,我們能挖掘出資料中隱藏但具有重要意義的資訊。由於本次資料集主要由類別型變數組成,如何將其適當地轉換為數值型變數,並進一步進行分析,是本專案的核心挑戰之一。不恰當的轉換可能導致資訊流失,因此選擇合適的處理方式至關重要,也是我們所學到的資料分析技巧。
感謝 Wang, Xuan-Chun 與 Sin, Wen-Lee 的協助分析,讓此專案能順利進行。
延伸學習
- 本文使用的 ipynb 檔案。
- 本文的 Github 儲存庫。
參考資料
Adil Shamim(2025年4月)。Math-Students Performance Data。Kaggle。2025年5月1日參考自 https://www.kaggle.com/datasets/adilshamim8/math-students
Cortez, P (2008)。Student Performance [Dataset]。UCI Machine Learning Repository。參考自 https://doi.org/10.24432/C5TG7T
Cortez, P., & Silva, A. M. (2008)。Using data mining to predict secondary school student performance。