戴克斯特拉演算法

封面圖片由 ChatGPT 生成。
前言
戴克斯特拉演算法(Dijkstra’s Algorithm)是探討最短路徑的一種演算法,最早是用於尋找兩點間的最短路徑,後拓展到由固定一點尋找與其他點的最短路徑,稱為該點的「最短路徑樹」。

運作原理
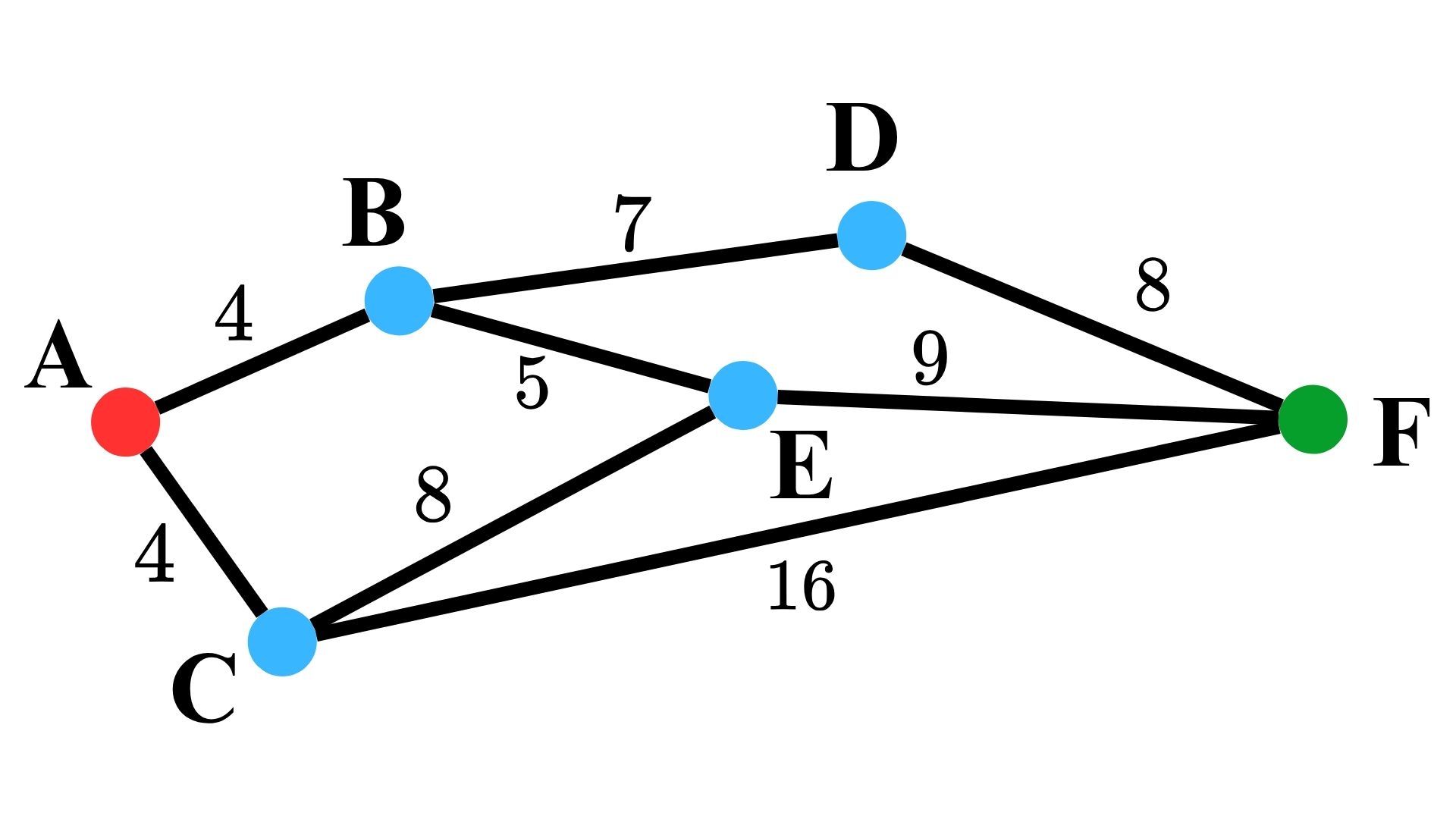
首先,計算各路徑的距離,如下圖所示。
為了找到從 $A$ 點出發的最短路徑,以下建立表格用於記錄路徑尋找過程中的前一個地點與距離。為了比較最短路徑,將距離的預設值寫為無窮大($\infty$),以用於比較大小。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | $\infty$ | ||
| B | $\infty$ | ||
| C | $\infty$ | ||
| D | $\infty$ | ||
| E | $\infty$ | ||
| F | $\infty$ |
因為出發點為 $A$ ,自己與自己的距離為 0 ,因此將表格中 $A$ 的距離記為 0 。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | 0 | ||
| B | $\infty$ | ||
| C | $\infty$ | ||
| D | $\infty$ | ||
| E | $\infty$ | ||
| F | $\infty$ |
接下來,檢查所有未標記的地點,找到未標記的地點中距離最短的那一個並進行標記,表示為最佳路徑。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | $\infty$ | ||
| C | $\infty$ | ||
| D | $\infty$ | ||
| E | $\infty$ | ||
| F | $\infty$ |
由前項計算完 $A$ 地點後,將與 $A$ 地點相鄰的所有地點的前一個地點記為 $A$ ,同時更新其距離。由先前的圖可以看到, $A$ 地點與 $B$ 和 $C$ 相鄰,且 4 小於預設距離 $\infty$ ,將其更新為 4 。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | 4 | A | |
| C | 4 | A | |
| D | $\infty$ | ||
| E | $\infty$ | ||
| F | $\infty$ |
接下來,再次重新尋找未標記的地點中距離最短的那一個並進行標記,表示為最佳路徑。可以看到目前 $B$ 和 $C$ 都擁有最短距離,這裡先標記 $B$ 。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | ✓ | 4 | A |
| C | 4 | A | |
| D | $\infty$ | ||
| E | $\infty$ | ||
| F | $\infty$ |
現在,更新 $B$ 地點相鄰的幾個地點 $D$ 和 $E$ 。從 $D$ 開始計算,可以發現 $A$ 經過 $B$ 抵達 $D$ 的距離為 $4 + 7 = 11$ , 11 比表格上 $D$ 的距離欄之值 $\infty$ 還小,將 11 更新取代 $\infty$ 並將前一個地點記為 $B$ ;而從 $A$ 經過 $B$ 再到 $E$ 的距離是 $9$ ,也小於 $\infty$,這裡也做相同的動作。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | ✓ | 4 | A |
| C | 4 | A | |
| D | 11 | B | |
| E | 9 | B | |
| F | $\infty$ |
接下來,繼續尋找未標記的地點中距離最短的那一個並進行標記,找到 $C$ 地點為距離最小,並嘗試更新其鄰近地點 $E$ 和 $F$ 。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | ✓ | 4 | A |
| C | ✓ | 4 | A |
| D | 11 | B | |
| E | 9 | B | |
| F | $\infty$ |
$E$ 和 $F$ 的距離為 12 和 20。我們可以發現到 F 的距離為 $C$ 點距離 $4$ 加上 $C 到 $F$ 的路徑長 16 ,得到 $ $20 < \infty$ ,更新 $F$ 的資訊;而 E 點的距離為 12 , 比表格上的距離欄位的 9 還大,不是最佳路徑,故不更新。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | ✓ | 4 | A |
| C | ✓ | 4 | A |
| D | 11 | B | |
| E | 9 | B | |
| F | 20 | C |
接下來重複標記未被標記的最短路徑,並更新其相鄰的地點,直到所有地點都被標記。最終可以得到如下表格。
| 地點 | 標記 | 距離 | 前一個地點 |
|---|---|---|---|
| A | ✓ | 0 | |
| B | ✓ | 4 | A |
| C | ✓ | 4 | A |
| D | ✓ | 11 | B |
| E | ✓ | 9 | B |
| F | ✓ | 18 | E |
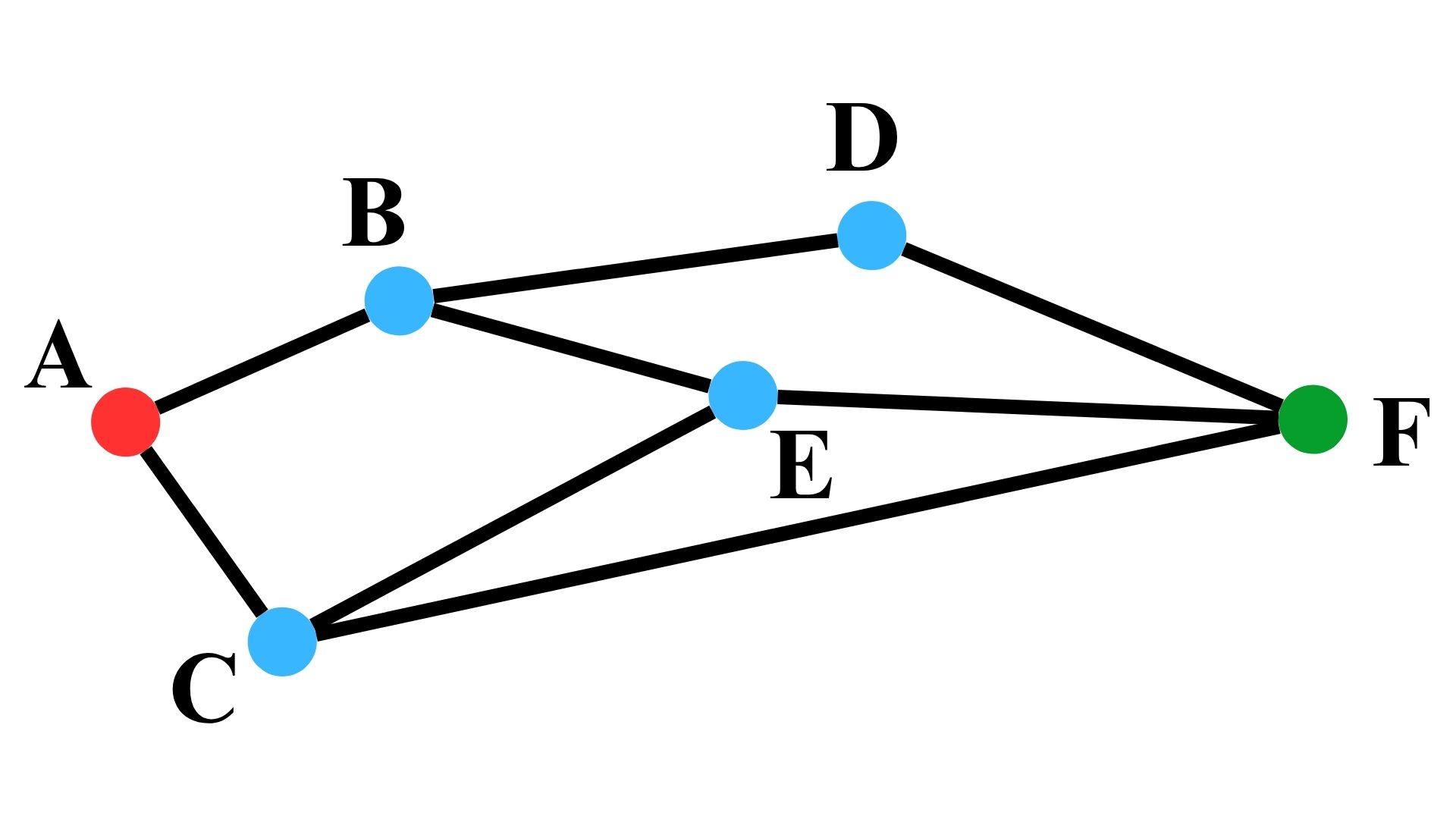
從以上表格,我們不僅可以知道最短路徑距離為 18 ,還能從終點 $F$ 反推最佳路徑到起點 $A$ 。由上表,可以知道最佳路徑為 $$ A \Rightarrow B \Rightarrow E \Rightarrow F $$
演算法
根據以上範例,可以大致總結戴克斯特拉演算法步驟如下:
- 從未標記的地點選擇距離起點的最短路徑。
- 標記該路徑。
- 計算經該路徑到其鄰近地點的距離。
- 若距離總長度小於目前所記錄的距離,更新該地點的距離,並記錄前一個地點;若距離總長度大於目前所記錄的距離,直接進行下一步。
- 回到第 1 步並重複執行,直到所有地點都被標記。
結語
初次見到這個演算法,讓我覺得大受震撼,原來我們所熟悉的最短路徑可以使用簡單的幾個步驟就可以算出來了。如果沒有見識到這一種演算法,或許我會很暴力的,將每一個點之間的距離都算出來吧?
參考資料
戴克斯特拉演算法。(2025年6月19日)。維基百科,自由的百科全書。2025年7月2日參考自 https://zh.wikipedia.org/zh-tw/戴克斯特拉算法
从0开始数。(2021年1月29日)。【算法】最短路径查找—Dijkstra算法 [影片]。YouTube。2025年7月2日參考自https://youtu.be/JLARzu7coEs