從梯度下降到隨機梯度下降

封面圖片由 ChatGPT 生成。
梯度下降是現今多數模型都會使用到的迭代方法,能夠幫助模型找到適合的參數。但對於現在的大數據時代,龐大的資料對梯度下降所帶來的後果就是巨大的時間成本,如何快速且不失準確性的計算參數是現今應要考慮的目標之一。
什麼是梯度
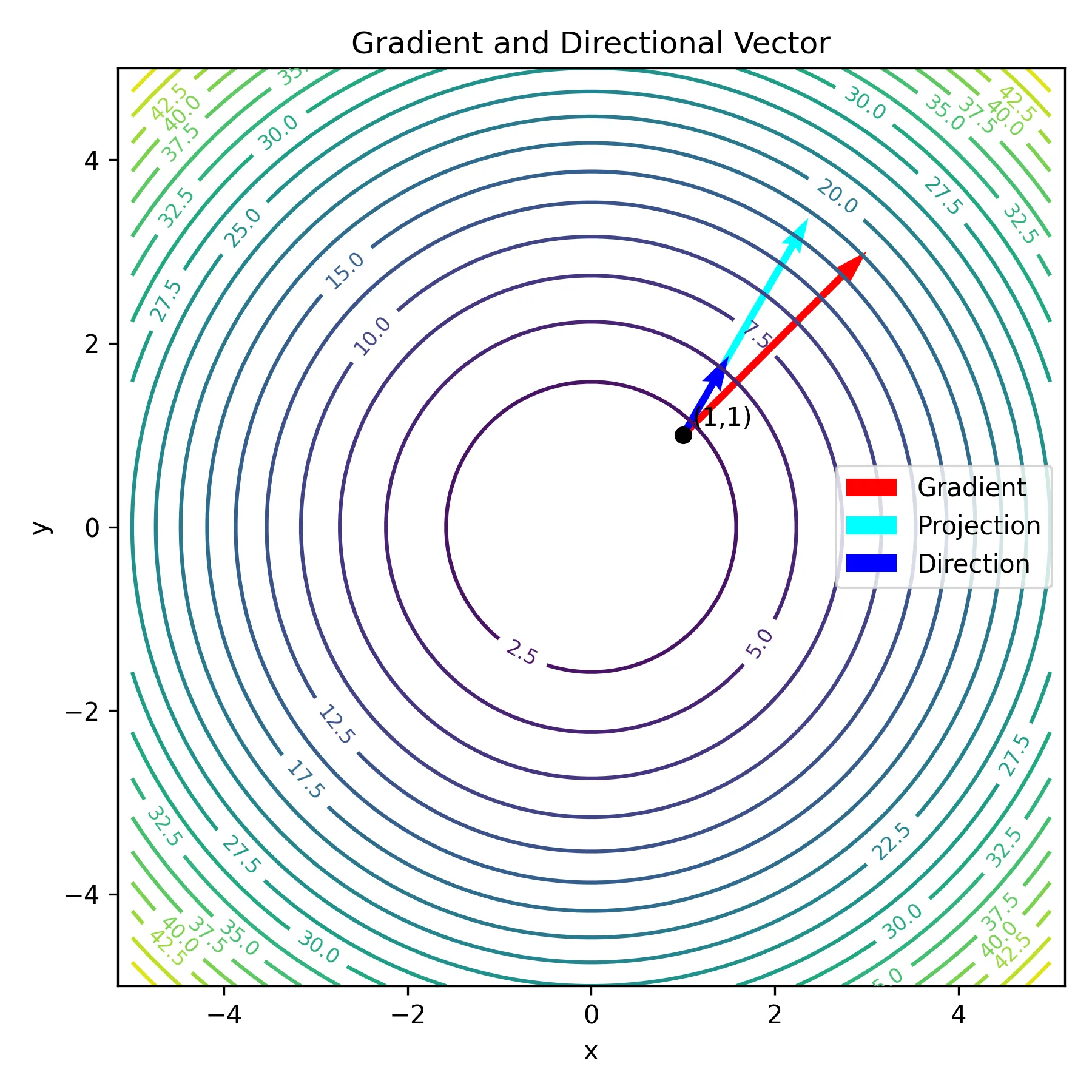
梯度(gradient)是多元函數導數的一種推廣,同時描述了函數在各個變數方向上的變化率。梯度向量指出了函數在某一點變化最快的方向,而其大小(範數)則代表在該方向上的變化速率。簡單來說,如果一維導數是曲線上某點的斜率,那麼梯度就是高維空間中「斜率」的向量化表達。
故在純量函數 $f: \mathbb{R}^n \to \mathbb{R}$ ,其梯度表示為 $\nabla f: \mathbb{R}^n \to \mathbb{R}^n$ ,其中 $\nabla$ 為向量微分算子。即
$$ \nabla f(\boldsymbol{x}) = \begin{pmatrix} \frac{\partial f}{\partial x_1}(\boldsymbol{x}) \\ \vdots \\ \frac{\partial f}{\partial x_n}(\boldsymbol{x}) \end{pmatrix} $$
其中, $\boldsymbol{x} = (x_i, \cdots, x_n)$ 。且
$$ \nabla f(\boldsymbol{x}) \cdot \boldsymbol{v} = \frac{\partial f}{\partial \boldsymbol{v}}(\boldsymbol{x}) = df_{\boldsymbol{x}}(\boldsymbol{v}) $$
其中, $\boldsymbol{v}$ 為任意單位向量,而 $df_{\boldsymbol{x}}(\boldsymbol{v})$ 則是函數 $f$ 在點 $\boldsymbol{x}$ 沿著方向 $\boldsymbol{v}$ 的變化率。
我們會希望使用梯度下降的方法來最小化損失函數(loss function),以便找到能夠最佳描述訓練資料的參數組合,用於逼近模型的最佳解。
梯度下降
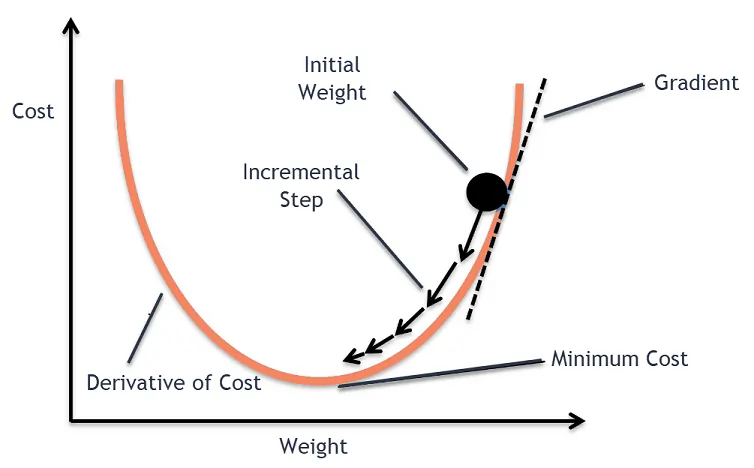
梯度下降(gradient descent, GD)是機器學習和深度學習中最基礎的優化演算法之一,用於在可微損失函數上尋找最小值。其方法為對於當前模型參數(權重與偏差)計算損失函數,而後沿負梯度方向更新參數。實務上所謂的梯度下降方法其實指的是批量梯度下降(Batch Gradient Descent, BGD),也就是用整個訓練資料集計算損失函數的梯度。
$$ w_{n + 1} = w_n - \eta \nabla L (w_n) $$
在上式中, $w_n$ 表示第 $n$ 次迭代的參數向量; $w_{n+1}$ 表示更新後的參數; $\eta > 0$ 為學習率(learning rate),控制更新步伐大小; $L(w)$ 是損失函數,用來衡量模型在訓練資料上的表現; $\nabla L(w_n)$ 是在當前參數 $w_n$ 下的梯度。透過不斷重複迭代多次,我們能逐步逼近損失函數的極小值。
若使用平均平方誤差(mean square error, MSE)作為計算與迭代權重參數的損失函數,假設 $(x_1, \cdots, x_m)$ 為輸入樣本向量,其中 $x_i \in \mathbb{R}^n$ 表示第 $i$ 筆樣本的特徵向量; $(y_1, \cdots, y_m)$ 為輸出標籤,其中 $y_i \in \mathbb{R}$ 表示第 $i$ 筆樣本的真實值;權重參數向量 $\boldsymbol{w} \in \mathbb{R}^n$ 。在不考慮偏差 $\varepsilon_i$ 的情況下,則損失函數可訂為
$$ L(\boldsymbol{w})=\frac{1}{2m}\sum_{i=1}^m (y_i - x_i^\top \boldsymbol{w})^2 $$
其中,使用 $2m$ 可使梯度計算較為簡潔。而梯度計算如下:
$$ \begin{align*} \nabla L(\boldsymbol{w}) & = \frac{1}{2m}\sum_{i=1}^m 2 (x_i^\top \boldsymbol{w} - y_i) x_i \\ & = \frac{1}{m}\sum_{i=1}^m (x_i^\top \boldsymbol{w} - y_i) x_i \end{align*} $$
隨著模型規模與資料量快速增長,需要計算所有參數才能計算梯度的 BGD 往往會導致運算速度緩慢且資源消耗過大。因此,隨機梯度下降及其變體被廣泛應用於實際任務中,以提高效率與收斂速度。
隨機梯度下降
相較於需要計算整個訓練資料集後才能更新參數的 BGD ,隨機梯度下降(stochastic gradient descent, SGD)每次迭代只隨機抽取一個訓練樣本來估計梯度並更新參數。也就是說,在第 $n$ 次迭代中,從訓練集中隨機選取索引 $i_n \in \{ 1, \cdots, m \}$ , 並只計算樣本 $(x_{i_n}, y_{i_n})$ 的梯度 $\nabla L_{i_n} (w_n)$ 用於更新參數。
$$ w_{n + 1} = w_n - \eta \nabla L_{i_n} (w_n) $$
如此,每處理一個樣本就更新一次模型參數。與 BGD 相比, SGD 更新頻率更高,但每次更新的梯度估計帶有較大隨機噪聲。這種隨機性一方面使得 SGD 有時能跳脫淺層局部極小值(local minima)或鞍點(saddle point),另一方面也使得其收斂軌跡不再單調,而是在最小值附近呈現震盪。隨著迭代次數增加,若採用適當的學習率衰減策略,SGD 最終能在期望意義下收斂至全域最優點或某個良好的局部最優解。
SGD 的主要優勢在於計算與記憶體效率,每次僅需讀取並計算單個樣本,使得在大規模資料集上訓練更加可行,同時在初期階段收斂速度往往快於 BGD。此外,隨機抽樣的特性也有助於避免陷入壞的局部極小值。
然而,因為梯度估計僅基於單個樣本,其波動較大,導致損失函數曲線在訓練過程中劇烈震盪,難以平滑收斂。若學習率設定過高,甚至可能因過度更新而發散。因此,實務上常採用逐漸衰減學習率等策略來穩定收斂。
小批量梯度下降
小批量梯度下降(Mini-batch Gradient Descent, MBGD)是一種介於 BGD 與 SGD 之間的方法。每次迭代時, MBGD 會先將訓練集隨機打亂後劃分為若干個小批次(batch),然後使用每個批次中的多個樣本同時計算梯度並更新參數。
與 BGD 相比,MBGD 每次更新只需使用部分資料,因此計算開銷更小;與 SGD 相比,每次更新又基於多個樣本而非單一樣本,能有效降低梯度估計的隨機波動,使更新方向更穩定。這種比 SGD 更穩定、比 BGD 更新更頻繁的運算策略,讓 MBGD 成為深度學習模型訓練的主流方法。
數學上,若第 $n$ 次迭代隨機選取一個小批次 $B_n \subset \{ 1, 2, \dots, m \}$,其大小為 $|B_n| = b$,則梯度估計為:
$$ \nabla L_{B_n}(w_n) = \frac{1}{b} \sum_{i \in B_n} (x_i^\top w_n - y_i) x_i $$
對應的參數更新規則為:
$$ w_{n+1} = w_n - \eta \nabla L_{B_n}(w_n) $$
其中, $b$ 是批次大小(batch size),常見取值如 $32, 64, 128$ 等; $B_n$ 表示在第 $n$ 次迭代中選取的批次索引集合。當 $b = 1$ 時,MBGD 退化為 SGD ;當 $b = m$ 時,則退化為 BGD 。
MBGD 的優點在於能夠充分利用並行運算的特性,使每個批次的計算可以在 GPU 上高效執行,大幅提升更新效率。與 SGD 相比, MBGD 的更新方向更加平滑,因此能有效避免參數在訓練過程中因梯度波動過大而產生的震盪。此外,由於每次僅使用部分樣本進行更新,小批次數據所帶來的隨機性可以幫助模型跳脫壞的局部極小值,從而提升整體的收斂效果。
然而, MBGD 也存在一定的缺點。最大的挑戰在於如何選擇合適的批次大小。如果批次過小,會導致梯度估計噪聲過大,使模型更新不穩定;反之,若批次過大,則會趨近於批量梯度下降,失去隨機性與效率上的優勢。因此,在實際應用中,批次大小的設定通常需要根據資料規模、硬體資源以及模型特性進行調整,以達到最佳的訓練效果。
三種方法比較
| 方法 | 每次迭代使用資料量 | 更新頻率 | 優點 | 缺點 | 適用情境 |
|---|---|---|---|---|---|
| 梯度下降 | 全部樣本 $m$ | 低 | 更新方向最精確、收斂平滑 | 運算成本高、記憶體需求大 | 小資料集、模型較簡單 |
| 隨機梯度下降 | 單一樣本 $1$ | 高 | 運算快速、可跳脫局部極小值 | 噪聲大、震盪明顯、需學習率衰減 | 大型資料集 |
| 小批量梯度下降 | 小批次 $b$ | 中 | 計算效率高、能並行運算、梯度較平滑 | 批次大小需調整。過大時退化為 BGD ,過小時退化為 SGD | 深度學習訓練主流方法 |
以下使用 $f(x) = (x - 3)^2$ 作為損失函數,並隨機生成資料進行梯度下降。其中, MBGD 使用的批次大小為 5 ,迭代次數為 50 ,學習率為 0.1 。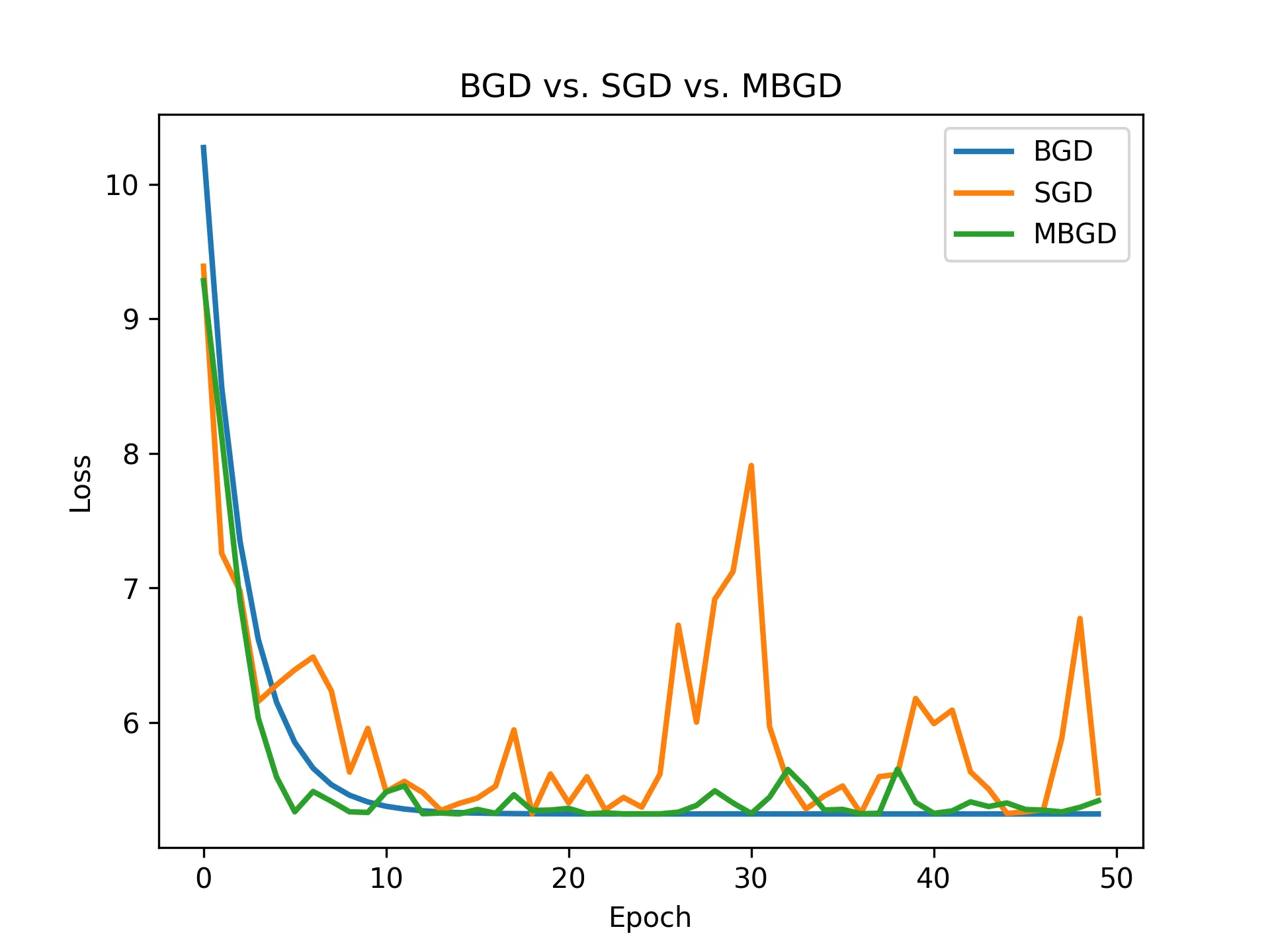
由圖中可以觀察到, BGD 每次更新方向最為精確,因此收斂過程平滑; SGD 則每次僅利用一個樣本進行更新,速度雖快,但梯度方向波動大,曲線呈現明顯震盪;相較之下, MBGD 綜合了兩者的優點,既能維持運算效率,又能得到相對穩定的收斂過程。
結語
實務中, MBGD 已成為深度學習模型訓練的標準做法,但隨著資料規模與模型複雜度持續增加,僅依靠單純的梯度下降方法已無法完全滿足需求。各種自適應學習率演算法(如 Adam、RMSProp、Adagrad 等)便是在 MBGD 的基礎上發展而來,進一步提升了收斂速度與穩定性。理解這些基礎方法之間的差異與優缺點,不僅有助於選擇合適的優化策略,也能幫助我們更好地理解深度學習訓練過程背後的數學原理。
延伸學習
- 本文使用的 Python 程式碼。
參考資料
- 梯度。(2025年7月4日)。維基百科,自由的百科全書。2025年8月30日參考自 https://zh.wikipedia.org/zh-tw/梯度
- Stochastic gradient descent。(2025年8月27日)。維基百科,自由的百科全書。2025年8月30日參考自 https://en.wikipedia.org/wiki/Stochastic_gradient_descent
- Tommy Huang(2018年7月31日)。機器/深度學習-基礎數學(三):梯度最佳解相關算法(gradient descent optimization algorithms)。Medium。2025年8月30日參考自 https://chih-sheng-huang821.medium.com/機器學習-基礎數學-三-梯度最佳解相關算法-gradient-descent-optimization-algorithms-b61ed1478bd7
- 劉智皓 (Chih-Hao Liu)(2021年6月4日)。機器學習_學習筆記系列(54):隨機梯度下降(Stochastic Gradient Decent)。Medium。2025年8月30日參考自 https://tomohiroliu22.medium.com/機器學習-學習筆記系列-54-隨機梯度下降-stochastic-gradient-decent-804229c968c
- 許皓翔(2023年9月27日)。【Day 12】優化器 Optimizer ( 一 )。iT 邦幫忙。2025年8月30日參考自 https://ithelp.ithome.com.tw/articles/10329190
- Alan Hsieh(2025年8月23日)。(Day 23) 深度學習中的優化方法 (Optimization in Deep Learning)。iT 邦幫忙。2025年8月30日參考自 https://ithelp.ithome.com.tw/articles/10375450
- Crypto1(2025年4月4日)。Gradient Descent Algorithm: How Does it Work in Machine Learning? Analytics Vidhya。2025年8月30日參考自 https://www.analyticsvidhya.com/blog/2020/10/how-does-the-gradient-descent-algorithm-work-in-machine-learning/