淺談貪婪演算法

封面圖片由 ChatGPT 生成。

前言

貪婪演算法（Greedy Algorithm）是一種透過每一步都選擇目前看起來最有利的選項進行求解的演算法，透過簡單且直觀地判斷在當前所有選擇中的最優解，並期望這些局部的選擇能累積成整體的最佳解，直到滿足終止條件為止。由於貪婪演算法僅專注於當下的局部環境，故選擇的解法不一定是全局的最優解，甚至可能會繞遠路。但不可否認的是，由於貪婪演算法不考慮全局，僅對局部選項做決策，因此通常具有相當高的執行效率。

運作原理

同戴克斯特拉演算法的範例，只不過這裡不尋找全局的最短路徑，而是尋找局部最短路徑。如上圖，假設現在有六個地點，依序為 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $F$ 。現在以 $A$ 點為起點， $F$ 點為終點，欲尋找 $A$ 點到 $F$ 點的路徑。

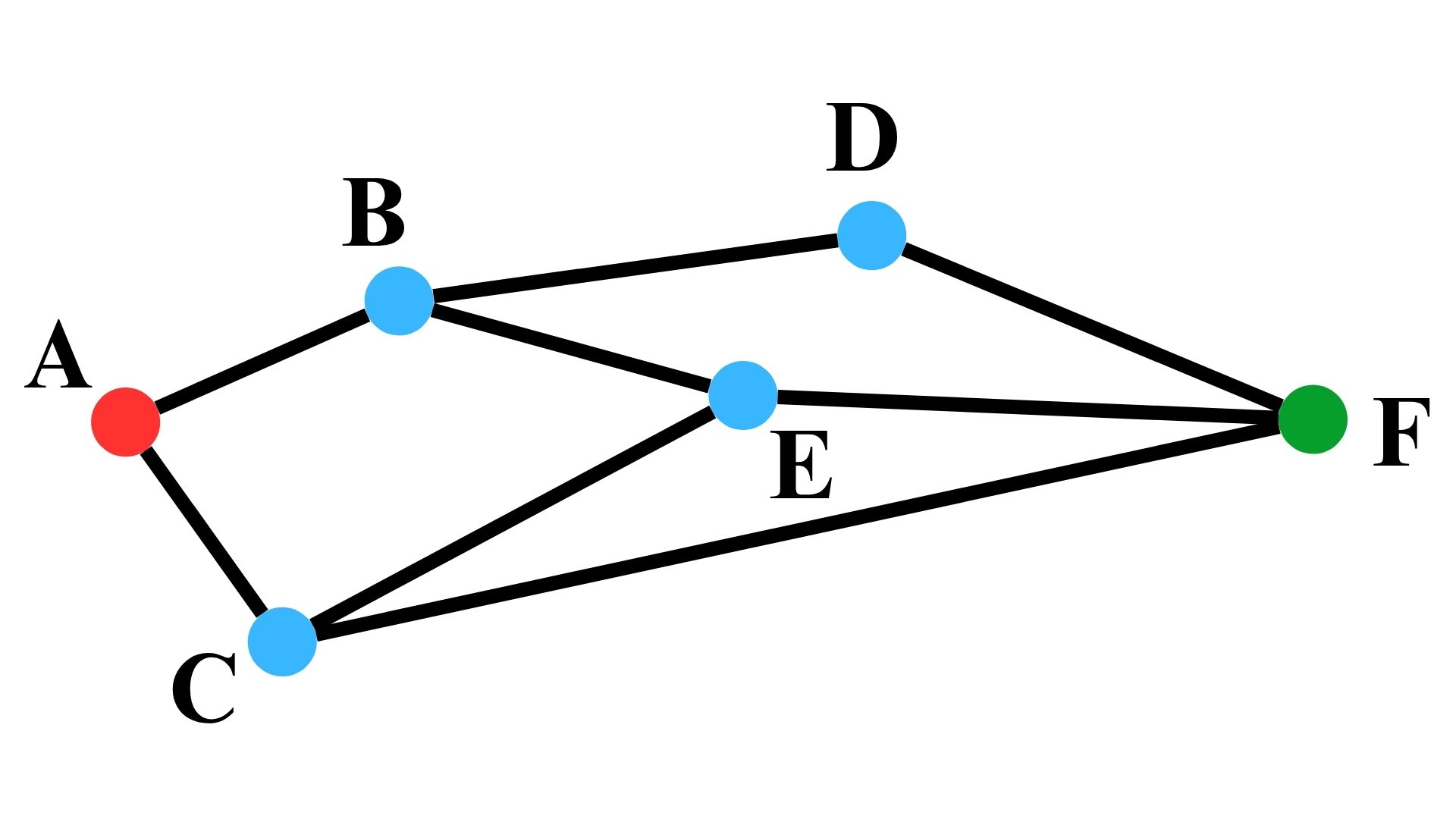
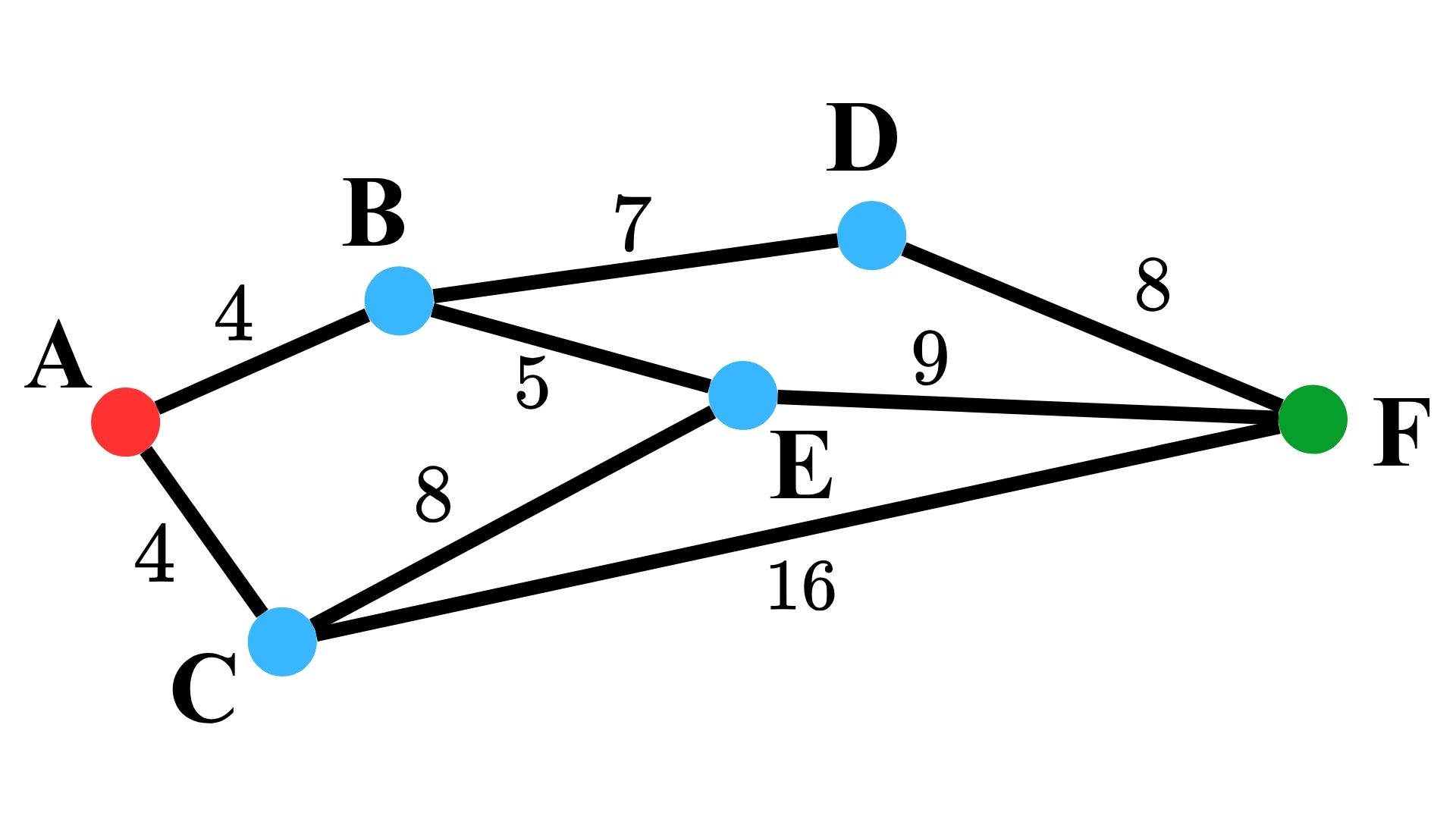
首先，計算各路徑的距離，如下圖所示。

為了找到從 $A$ 點出發到達 $F$ 點的路徑，以下建立表格用於記錄路徑尋找過程中的前一個地點。

地點	標記	前一個地點
A
B
C
D
E
F

因為出發點為 $A$ ，因此標記 $A$ 。

地點	標記	前一個地點
A	✓
B
C
D
E
F

接下來，判斷與 $A$ 點相鄰但未被標記的 $B$ 點與 $C$ 點路徑，尋找最短路徑。發現路徑長相同，我們先選擇 $B$ 點做運算。

將 $B$ 點做標記，並記錄前一個地點為 $A$ 。

地點	標記	前一個地點
A	✓
B	✓	A
C
D
E
F

現在，繼續判斷與 $B$ 點相鄰但未被標記的點，如 $D$ 點與 $E$ 點路徑。發現到 $E$ 點的路徑最短，標記 $E$ 點並做記錄。

地點	標記	前一個地點
A	✓
B	✓	A
C
D
E	✓	B
F

繼續判斷與 $E$ 點相鄰但未被標記的點，如 $C$ 點與 $F$ 點路徑。發現到 $C$ 點的路徑最短，標記 $C$ 點並做記錄。

地點	標記	前一個地點
A	✓
B	✓	A
C	✓	E
D
E	✓	B
F

最後，我們發現與 $C$ 點相鄰但未被標記的點只剩下 $F$ 點，標記 $F$ 點後我們可以得到如下表格。

地點	標記	前一個地點
A	✓
B	✓	A
C	✓	E
D
E	✓	B
F	✓	C

從以上表格，我們可以知道由貪婪演算法求得的最短路徑為 $$ A \Rightarrow B \Rightarrow E \Rightarrow C \Rightarrow F, $$

其距離為 $4 + 5 + 8 + 16 = 33$ ，相較於使用戴克斯特拉演算法所求得的路徑 $A \Rightarrow B \Rightarrow E \Rightarrow F$ 的距離 18 還遠。但我們可以發現，在貪婪演算法下，計算成本大幅下降，僅需比較該地點前往下個地點當下的成本，而不需維護全域狀態或重複更新距離。因此，在資源有限、對即時性要求較高的應用中，貪婪演算法依然有其價值，即便貪婪法不能保證全域最佳解，它仍被廣泛用於各種近似解法。

演算法

根據以上範例，可以大致總結貪婪演算法步驟如下：

1. 從目前所在的地點出發，在相鄰的地點中，選擇未標記且權重、路徑最佳（如最小權重或最大效益）的一個地點。
2. 移動至該處並標記該路徑。
3. 回到第 1 步並重複執行，直到符合終止條件（抵達終點等）。

結語

相較於戴克斯特拉演算法需要對全局資訊更新，計算成本相對較高昂，貪婪演算法則以其單純的決策機制，提供了一種更快速但不保證全局最優解的解法策略。雖然它在某些情況下可能產生次佳解，甚至繞遠路，但在運算資源有限或需要即時反應的場景中，貪婪演算法往往能展現高效的表現。貪婪演算法是一種簡潔而強大的策略工具，雖然不適用於所有問題，但只要掌握其特性與限制，便能在適當的場景下有效應用，達成速度與品質的平衡。

參考資料

• 貪婪演算法。（2022年10月31日）。維基百科，自由的百科全書。2025年7月7日參考自 https://zh.wikipedia.org/zh-tw/贪心算法

• 拉爾夫的技術隨筆。（2022年9月6日）演算法學習筆記：貪婪演算法（Greedy Algorithm）。Medium。2025年7月7日參考自 https://medium.com/@ralph-tech/演算法學習筆記-貪婪演算法-greedy-algorithm-e2666b93d05f

• Sean Chou。（2024年8月15日）演算法筆記系列 — Greedy Algorithm 貪婪演算法。Medium。2025年7月7日參考自 https://medium.com/技術筆記/演算法筆記系列-greedy-algorithm-貪婪演算法-236f509200de