文章
文章 標籤 分類
夥伴
關於
關於作者 隱私權政策
更多
有趣 工具 實用網站 留言板 時間旅行

目錄

k-平均聚類分析

 收錄於 機器學習
 發佈於   更新於    約 2990 字   預計閱讀 6 分鐘   次閱讀
https://raw.githubusercontent.com/Josh-test-lab/website-assets-repository/refs/heads/main/posts/k-means%20clustering/cover%20image.png

封面圖片由 ChatGPT 生成。

前言

k-平均聚類分析（k-means clustering），在中文地區常被稱為 k-平均演算法，簡稱 k-means。這是一種將 $n$ 個資料點分成 $k$ 個群集（clusters）的分群方法，使得每一個點都能歸屬於距離它最近的群集中心（centroid）。

在機器學習的分類中，k-means 屬於非監督式學習（unsupervised learning），因為它在訓練過程中不需要任何資料標籤（label），僅透過計算資料點之間的距離來進行分群。這種方式有點類似人類社會中人們自然形成的小團體：沒有預先的分類規則，僅根據彼此的相似程度自動聚在一起。

K-means 原理

假設有一個資料集 $$ x_1, x_2, \cdots, x_n $$

其中，每一個資料值 $x_i \in \mathbb{R}^d$ ， $i = 1, 2, \cdots, n$。為了將 $n$ 個資料點分配到鄰近的 $k$ 個群集，我們需要知道對於單一點 $x_i$ 來說， $x_i$ 距離哪一個群集中心最近，以將 $x_i$ 分配到該群集。

在此之前，我們得先決定群集中心的初始值。隨機給定 $k$ 個點作為群集中心，接下來就可以計算點 $x_i$ 距離哪一個中心點最近，而將該點歸類到某一群中。至於計算距離的方法，可以使用各種不同的距離度量方法，例如歐式距離。

待每一個點都計算並分類到最近的群集中心後，由各群集重新計算新的群集中心，群中心的算法為計算該群各維度的平均值所得到的那一個點坐標。接下來，重複將點重新分配到群集、找群集中心這些步驟。

最後，當新找出的群集中心不再變化，或是中心點的變化已經小到可以忽略不計時，就完成 k-means 的運算了，而找到群集中心這個步驟，可以看作是將 $n$ 個點分配到 $k$ 個集合中，使得每個集合內的平方和（within-cluster sum of squares, WCSS）最小，可以以下列公式表示：

$$ \argmin_\mathbf{S} \sum_{j=1}^k \sum_{x \in S_j} \| x - \mu_j \|^2, $$

其中， $\mathbf{S}$ 為包含所有點的集合， $\mathbf{S} = \{S_1, S_2, \cdots, S_k\}$ ， $S_j$ 為各群集， $j = 1, 2, \cdots, k$ ， $\mu_j$ 為群集 $S_j$ 的中心， $x$ 為群集 $S_j$ 中的所有點，且各群集內所擁有的點數量不一定一樣多，也就是 $|S_j| \neq |S_m|$ 。

演算法

簡單來說， k-means 演算法的公式如下：

  1. 隨機設定 $k$ 個點作為群集中心。
  2. 計算每一個點到各群集中心的距離。
  3. 將各點分配到最近的群集中心。
  4. 計算分配到群集的資料點的各維度平均值，找出新的群集中心。
  5. 比較新的群集中心與原本的群集中心是否有所差異，如果差異不大就停止演算法，否則回到步驟 2 。

Python 範例

https://raw.githubusercontent.com/Josh-test-lab/kmeans-example/refs/heads/main/kmeans_iris_iter/kmeans_iterations.gif
K-means 範例。

資料集說明

以下將使用 Iris 資料集作為範例， Iris 資料集是一個經典的機器學習與統計分析資料集，常被用於分類與視覺化的練習，其目標為預測鳶尾花（iris flower）的品種。

在此資料集中，包含：

  • 樣本數：150 筆。
  • 特徵數：4 個數值型特徵。
    • 花萼長度（sepal length，單位：公分）
    • 花萼寬度（sepal width，單位：公分）
    • 花瓣長度（petal length，單位：公分）
    • 花瓣寬度（petal width，單位：公分）
  • 類別數：3 種花的品種。
    • 山鳶尾（setosa）
    • 變色鳶尾（versicolor）
    • 維吉尼亞鳶尾（virginica）

前置準備

在 Python 中，我們可以從 sklearn 模組讀取 Iris 資料集。在以下範例中，我們使用後兩個特徵值，也就是花瓣長度與花瓣寬度作為視覺化的分類項目。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# import modules
import numpy as np
import matplotlib.pyplot as plt
import os
from sklearn.datasets import load_iris
from sklearn.metrics import pairwise_distances_argmin

# Iris data
iris = load_iris()  # load data
X = iris.data[:, 2:]  # data
y_true = iris.target  # target
class_names = iris.target_names  # Iris class names

print(f'\nclass names: \n{class_names}')
print(f'\nfeature names: \n{iris.feature_names}')
執行結果參考
1
2
3
4
5

class names: 
['setosa' 'versicolor' 'virginica']

feature names: 
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

以下設定需要的分類數量。由於我們已知鳶尾花共有 3 種，因此這裡直接將真值數量 true_clusters 由資料集形狀讀取，並設定需要分群的數量 n_clusters 為 3 。如想要試試分成更多群集，也可以調整 n_clusters 。

1
2
3
4
5
6

# configs
true_clusters = iris.target_names.shape[0]  # true clusters
n_clusters = 3  # number of clusters we want to classify

output_dir = 'kmeans_iris_iter'  # output directory
os.makedirs(output_dir, exist_ok=True)

以下設定真值得群集中心，方便後續比較 k-means 的分群效果。同時，設定不同顏色，方便後續視覺化比較。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

# true centers
true_centers = np.array([X[y_true == i].mean(axis=0) for i in range(true_clusters)])

print(true_centers)

# colors
cmap = plt.get_cmap('tab10')
colors = [cmap(i) for i in range(max(true_clusters, n_clusters))]

# markers
markers = ['o', 's', 'D']
執行結果參考
1
2
3
4
5
6

# colors
cmap = plt.get_cmap('tab10')
colors = [cmap(i) for i in range(max(true_clusters, n_clusters))]

# markers
markers = ['o', 's', 'D']

真值散佈圖

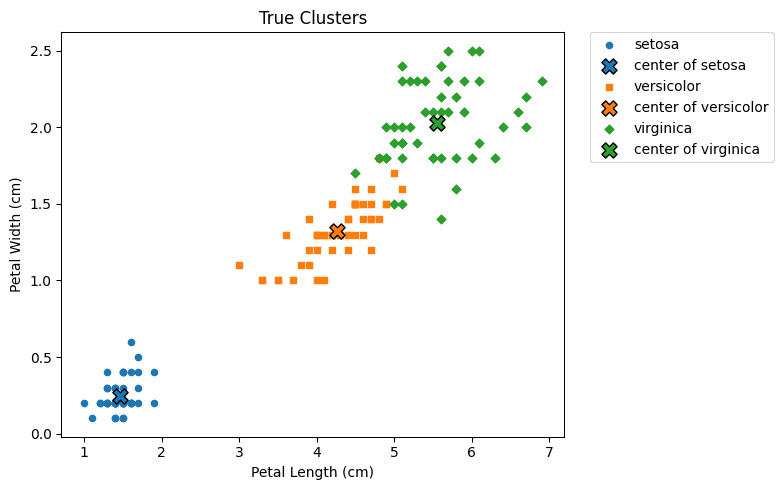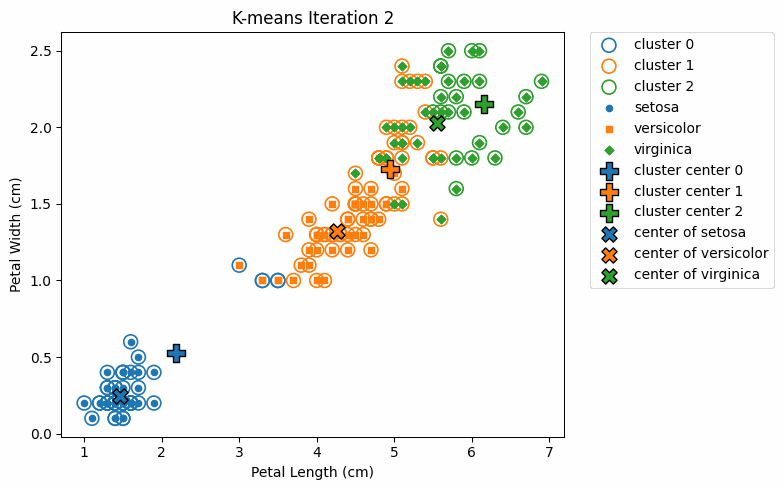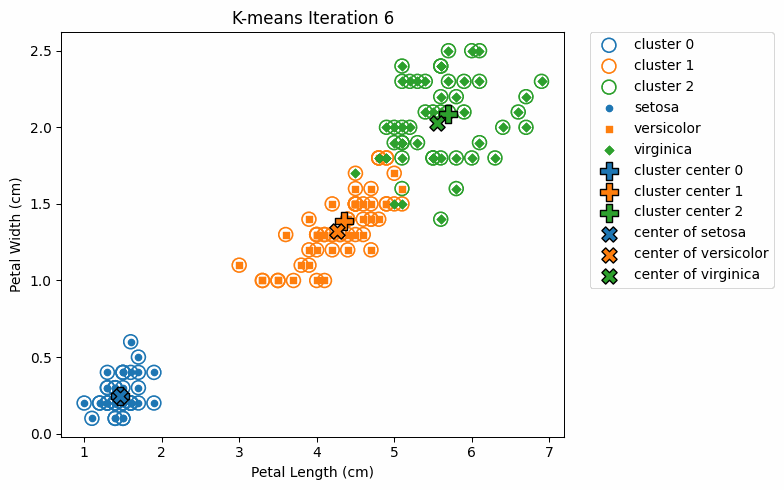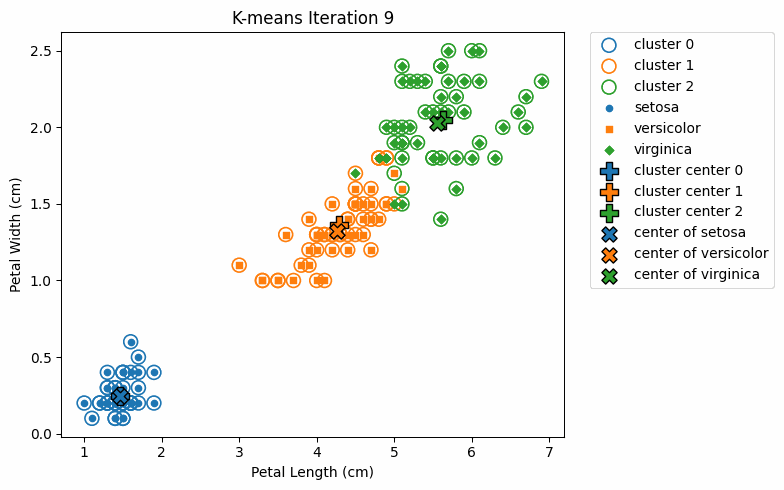
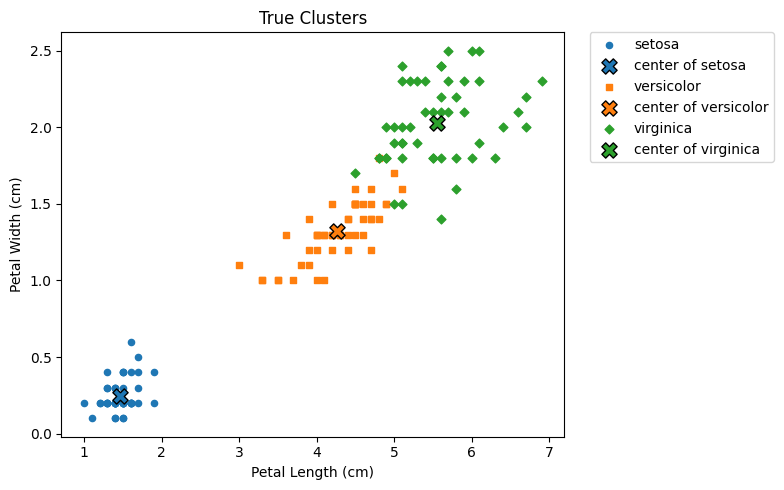
做好前置準備後，現在繪製實際的鳶尾花分類情形，如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

# plot of true values
plt.figure(figsize=(8, 5))
for i in range(true_clusters):
    # true values
    plt.scatter(X[y_true == i, 0], X[y_true == i, 1], color=colors[i], marker=markers[i], s=20, label=f'{class_names[i]}')
    # true centers
    plt.scatter(true_centers[i, 0], true_centers[i, 1], color=colors[i], marker='X', edgecolor='black', s=120, label=f'center of {class_names[i]}')

plt.title(f'True Clusters')
plt.xlabel('Petal Length (cm)')
plt.ylabel('Petal Width (cm)')
plt.legend(loc='upper left', bbox_to_anchor=(1.05, 1.0), borderaxespad=0)
plt.tight_layout()
plt.savefig(f'{output_dir}/true.png', bbox_inches='tight')
plt.show()
plt.close()

https://raw.githubusercontent.com/Josh-test-lab/kmeans-example/refs/heads/main/kmeans_iris_iter/true.png
鳶尾花使用花瓣特徵值分類的真實值。

如上圖，藍色表示山鳶尾，橘色表示變色鳶尾，綠色表示維吉尼亞鳶尾；而 ✕ 表示各群集中心。

K-means

首先，初始化群集中心。這裡固定種子為 123 ，並隨機選取 n_clusters 個值作為分類的群集中心。

1
2
3
4

# initialize k-means center points
np.random.seed(123)  # set random seed
init_idx = np.random.choice(len(X), size=n_clusters, replace=False)
centers = X[init_idx]

接下來，就可以進行迭代訓練並找出群集中心。以下將在迭代的同時，繪製各迭代的圖片，方便觀察群集中心的移動，並且也將真值繪製於圖上。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# k-means
iteration = 0
while True:
    # assign each point to the nearest center
    labels = pairwise_distances_argmin(X, centers)

    plt.figure(figsize=(8, 5))
    # cluster values
    for i in range(n_clusters):
        plt.scatter(X[labels == i, 0], X[labels == i, 1], facecolors='none', edgecolors=colors[i], linewidths=1.2, s=100, label=f'cluster {i}')

    # true values
    for i in range(true_clusters):
        plt.scatter(X[y_true == i, 0], X[y_true == i, 1], color=colors[i], marker=markers[i], s=20, label=f'{class_names[i]}')
    
    # cluster centers
    for i in range(n_clusters):
        plt.scatter(centers[i, 0], centers[i, 1], color=colors[i], marker='P', edgecolor='black', s=180, label=f'cluster center {i}')

    # true centers
    for i in range(true_clusters):
        plt.scatter(true_centers[i, 0], true_centers[i, 1], color=colors[i], marker='X', edgecolor='black', s=120, label=f'center of {class_names[i]}')

    plt.title(f'K-means Iteration {iteration}')
    plt.xlabel('Petal Length (cm)')
    plt.ylabel('Petal Width (cm)')
    plt.legend(loc='upper left', bbox_to_anchor=(1.05, 1.0), borderaxespad=0)
    plt.tight_layout()
    plt.savefig(f'{output_dir}/kmeans_iter_{iteration:02d}.png', bbox_inches='tight')
    plt.show()
    plt.close()

    # update cluster centers
    new_centers = np.array([X[labels == i].mean(axis=0) if np.any(labels == i) else centers[i] for i in range(n_clusters)])

    # stop condition
    if np.sum((new_centers - centers)**2) < 1e-20:
        break
    
    # next iteration
    centers = new_centers
    iteration += 1

最後，整個迭代過程如下顯示：

gallery_made_with_nanogallery2-kmeans

在上圖中，實心點表示各鳶尾花種的實際分類，而空心圓圈 ◯ 則表示分類的群集； ✕ 表示各花種的真實中心，而 ✛ 則表示各分類群集的中心。

我們可以發現，在每次的迭代過程中，分類所得的群集中心 ✛ 逐漸接近真實中心 ✕。雖然在邊界區域仍出現少數分類錯誤的情況，但整體而言，k-means 在大多數區域已能正確地將資料點分配至對應的群集。

結語

k-means 演算法是一種簡單且高效的分群方法，廣泛應用於圖像處理、市場區隔、生物資訊等多種領域。透過反覆地更新群集中心與重新分配資料點，k-means 能夠在不需要標籤資料的情況下，自動找出潛在的結構與模式。

雖然 k-means 在許多情況下表現良好，但它也存在一些限制，例如對初始中心點敏感、只能處理凸型群集，以及對離群值較為脆弱等。因此，在實際應用中，我們需根據資料特性謹慎選擇演算法，或考慮與其他方法搭配使用，以獲得更穩定與準確的分群結果。

運行環境

  • 作業系統：Windows 11 24H2
  • 程式語言：Python 3.12.9

延伸學習

參考資料

更新於 2025-07-11 20:17 UTC+0800   4cbde75d
Creative Commons License
 演算法, 機器學習
返回 | 首頁