邏輯迴歸

封面圖片由 ChatGPT 生成。

前言

邏輯迴歸（logistic regression），又稱為邏輯斯迴歸、羅吉斯迴歸，是由線性迴歸（linear regression）變化而成的一種二元分類模型。與線性迴歸模型不同的是，線性迴歸會找出一條能夠穿越所有數據點的迴歸線，且每個點到迴歸線的平方和是最小的，稱為最小平方法（least squares method）；而邏輯迴歸模型的目標則是找出一條迴歸線，使迴歸線能夠明確地將所有數據點分為兩類。

勝算與勝算比

提到邏輯迴歸，就不得不先提到勝算與勝算比這兩個概念。

勝算

若某事件在特定條件下發生的機率為 $p$，則其勝算（odds）定義為該事件發生的機率與不發生的機率之比值：

$$ \text{odds} = \frac{p}{1 - p} $$

也就是說，若勝算為 $w$，表示事件發生的機會是未發生的 $w$ 倍。

勝算比

勝算比（odds ratio, OR）是兩組勝算的比值，通常比較「有某特徵」與「無此特徵」的情況下事件發生的機率差異：

$$ \text{OR} = \frac{\text{odds}_1}{\text{odds}_2} = \frac{p_1 / (1 - p_1)}{p_2 / (1 - p_2)} $$

由勝算比，我們可以得知

• 若 OR $> 1$：表示在特定條件下，事件發生的可能性較高。
• 若 OR $= 1$：表示在特定條件下，事件發生的可能性和沒有該條件時相同，與事件無關。
• 若 OR $< 1$：表示在特定條件下，事件發生的可能性較低。

邏輯與邏輯函數

邏輯

邏輯（logit / logit function）與勝算息息相關，其源於邏輯轉換（logit transformation），是將介於 0 到 1 之間的值映射到實數線 $\mathbb{R}$ 上，定義如下：

$$ \text{logit}(p) = \ln \left( \frac{p}{1 - p} \right) $$

因此邏輯可以理解為「勝算的對數」。這個轉換讓我們能將原本非線性的機率問題轉換為一個線性的預測模型。

而任意兩機率 $p_1$ 與 $p_2$ 的邏輯的差也可以被證明為勝算比的對數：

邏輯函數

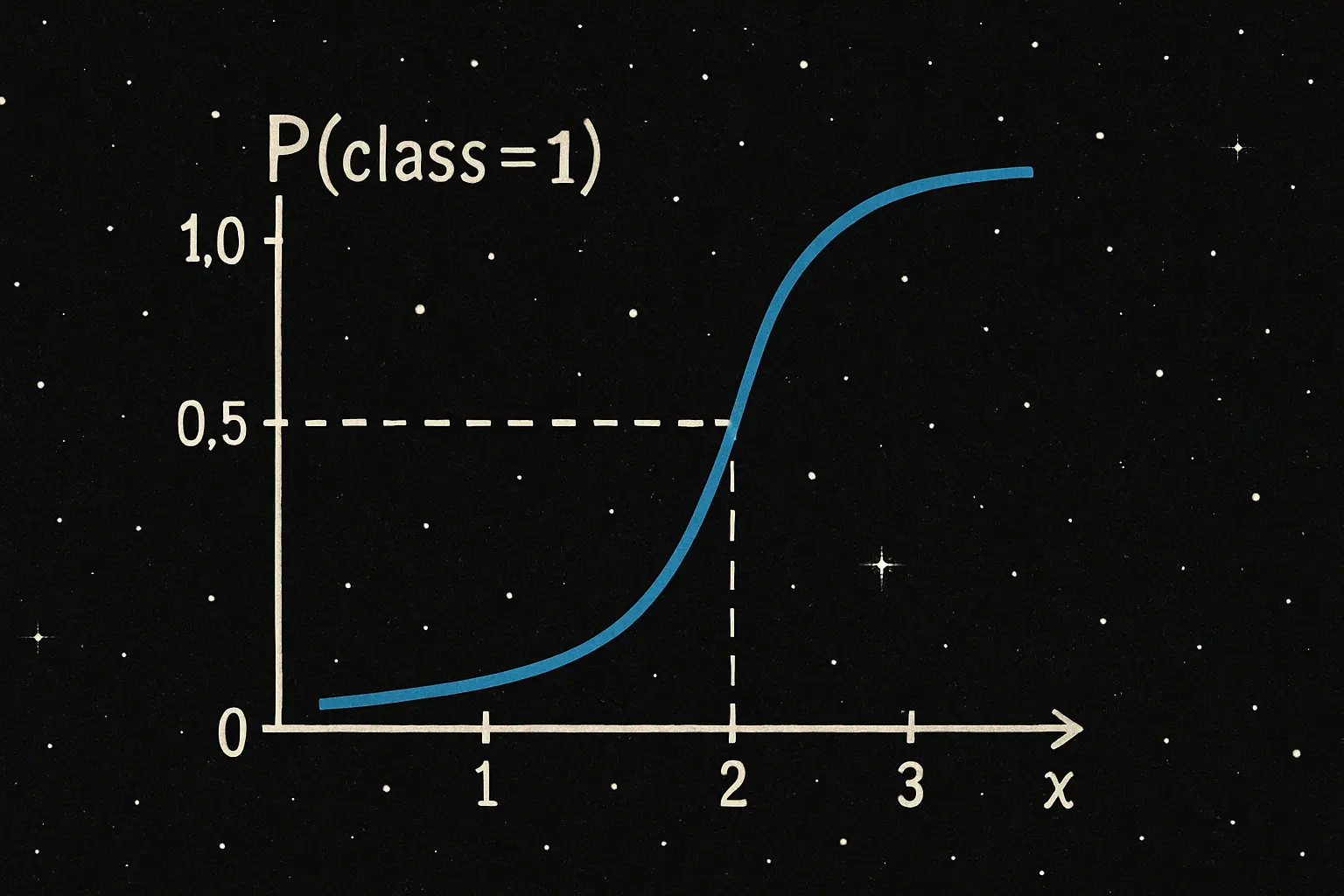
邏輯函數（logistic function）是邏輯迴歸的核心，也稱為 S 型函數（sigmoid function）。其公式如下：

$$ \sigma(x) = \frac{1}{1 + e^{-x}} $$

邏輯函數的輸入值 $x$ 可為任意實數，輸出值則會被限制在 $[0, 1]$ 。

邏輯迴歸

現在，假設應變數 $Y$ 是一個二元隨機變數，且 $Y \in [0, 1]$ 。其中 $1$ 表示事件成功， $0$ 表示失敗。令 $Y = f(\boldsymbol{X})$ ，其條件機率用邏輯建立：

$$ \begin{align*} f(\boldsymbol{X}) & = \ln \left( \frac{\boldsymbol{p}}{1 - \boldsymbol{p}} \right) \\ & = \begin{bmatrix} \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + \cdots + \beta_n x_{1n} \\ \beta_0 + \beta_1 x_{21} + \beta_2 x_{22} + \cdots + \beta_n x_{2n} \\ \vdots \\ \beta_0 + \beta_1 x_{m1} + \beta_2 x_{m2} + \cdots + \beta_n x_{mn} \\ \end{bmatrix}_{m \times 1} \\ & = \boldsymbol{X} \boldsymbol{\beta} \end{align*} $$

其中， $\boldsymbol{X}$ 為含常數項的輸入變數矩陣（自變數矩陣），每列為一筆資料，第一欄為常數項 $1$，其餘為 $n$ 個自變數（特徵）； $\boldsymbol{\beta} = (\beta_0, \beta_1, \beta_2, \cdots, \beta_n)^\top$ 為係數向量。

$$ \boldsymbol{X} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1n} \\ 1 & x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m1} & x_{m2} & \cdots & x_{mn} \end{bmatrix}_{m \times (n+1)} $$

而 $\boldsymbol{p} = \Pr(Y = 1 \mid \boldsymbol{X}) = (p_1, \cdots, p_m)$ 為事件成功的機率向量。我們可以從前次的證明，套用邏輯函數得到 $\boldsymbol{p}$ 的估計值 $\hat{\boldsymbol{p}}$ 為

$$ \hat{\boldsymbol{p}} = \sigma(f(\boldsymbol{X})) = \sigma(\boldsymbol{X} \boldsymbol{\beta}) = \frac{\exp(\boldsymbol{X} \boldsymbol{\beta})}{1 + \exp(\boldsymbol{X} \boldsymbol{\beta})} $$

同理，事件失敗的機率 $1 - \hat{\boldsymbol{p}} = \Pr(Y = 0 \mid \boldsymbol{X})$ 也可寫作

$$ 1 - \hat{\boldsymbol{p}} = \frac{1}{1 + \exp(\boldsymbol{X} \boldsymbol{\beta})} $$

損失函數

對於邏輯迴歸，損失函數（loss function）常用交叉熵（cross-entropy）。由於應變數 $Y$ 是二元變量，因此此處使用離散變量的交叉熵，其公式如下。

$$ \text{entropy} = -y \ln (p) $$

其中， $y$ 是分佈， $p$ 是機率。因此，對於單一變數的損失函數可以定義如下：

$$ \begin{align*} L(y_i, \hat{p_i}) & = \left\{\begin{matrix} -\ln (\hat{p_i}), & \text{if } y_i = 1; \\ -\ln (1 - \hat{p_i}), & \text{if } y_i = 0. \end{matrix}\right. \\ & = -y_i \ln (\hat{p_i}) - (1 - y_i) \ln (1 - \hat{p_i}) \end{align*} $$

其中， $i = 1, \cdots, m$ ， $\hat{p}_i = \sigma(X_i^\top \boldsymbol{\beta})$ ， 是第 $i$ 筆資料的預測機率， $X_i = (1, x_{i1}, x_{i2}, \cdots, x_{in})^\top$ ， $\boldsymbol{\beta} = (\beta_0, \beta_1, \beta_2, \cdots, \beta_n)^\top$ 。

對於前述的整個樣本資料集 $\boldsymbol{X}$ 矩陣，損失函數定義如下：

$$ \begin{align*} L(Y, \hat{\boldsymbol{p}}) & = \sum_{i = 1}^m \left[ -y_i \ln (\hat{p_i}) - (1 - y_i) \ln (1 - \hat{p_i}) \right] \\ & = -\sum_{i = 1}^m \left[ y_i \ln(\sigma(X_i^\top \boldsymbol{\beta})) + (1 - y_i) \ln(1 - \sigma(X_i^\top \boldsymbol{\beta})) \right] \\ & = -\sum_{i = 1}^m y_i \ln(\sigma(X_i^\top \boldsymbol{\beta})) -\sum_{i = 1}^m (1 - y_i) \ln(1 - \sigma(X_i^\top \boldsymbol{\beta})) \\ & = -\sum_{y_i = 1} \ln(\sigma(X_i^\top \boldsymbol{\beta})) -\sum_{y_i = 0}\ln(1 - \sigma(X_i^\top \boldsymbol{\beta})) \\ & = -\sum_{y_i = 1} \ln(\hat{p_i}) -\sum_{y_i = 0}\ln(1 - \hat{p_i}) \end{align*} $$

其中， $X_i = (1, x_{i1}, x_{i2}, \cdots, x_{in})^\top$ ， $Y = (y_1, y_2, \cdots, y_m)^\top$ ， $i = 1, \cdots, m$ 。

概似函數

因為 $\boldsymbol{X}$ 是固定的已知變數，為了降低誤差，也就是讓損失函數趨近於 0 ，我們實際上是在尋找一組最佳係數 $\boldsymbol{\beta}$ ，使模型預測的機率 $\hat{\boldsymbol{p}}$ 與觀測值 $Y$ 最接近。

假設觀測值 $Y$ 中的每筆樣本 $y_i$ 條件獨立，並服從伯努利分佈（Bernoulli distribution），則各樣本的機率密度函數為

$$ \Pr(y_i \mid X_i, \boldsymbol{\beta}) = \hat{p}_i^{y_i} (1 - \hat{p_i})^{1 - y_i} $$

因此，概似函數（likelihood function）可寫為

$$ \mathcal{L}(\boldsymbol{\beta}) = \prod_{i = 1}^m \hat{p}_i^{y_i} (1 - \hat{p_i})^{1 - y_i} $$

對數概似函數

為了找到最佳係數 $\boldsymbol{\beta}$ ，我們會對概似函數 $\mathcal{L}(\boldsymbol{\beta})$ 取一階導數，找到其極大值所對應的係數，這個方法稱作最大概似估計。

然而，由於概似函數中包含大量的連乘符號 $\prod$，不利於計算與推導，因此我們通常對概似函數取對數，將乘積轉換為加總，用於簡化計算，稱為對數概似函數（log-likelihood function）。計算方式如下：

$$ \begin{align*} \ell(\boldsymbol{\beta}) & = \ln (\mathcal{L}(\boldsymbol{\beta})) \\ & = \ln \left( \prod_{i = 1}^m \hat{p}_i^{y_i} (1 - \hat{p_i})^{1 - y_i} \right) \\ & = \sum_{i=1}^m \left( \ln \left( \hat{p}_i^{y_i} (1 - \hat{p_i})^{1 - y_i} \right) \right) \\ & = \sum_{i=1}^m \left[ \ln \left( \hat{p}_i^{y_i} \right) + \ln \left( (1 - \hat{p_i})^{1 - y_i} \right) \right] \\ & = \sum_{i=1}^m \left[ y_i \ln(\hat{p}_i) + (1 - y_i) \ln(1 - \hat{p}_i) \right] \\ & = \sum_{y_i = 1} \ln(\hat{p_i}) + \sum_{y_i = 0}\ln(1 - \hat{p_i}) \end{align*} $$

最大概似估計

從先前的計算，我們會發現 $$ L(Y, \hat{\boldsymbol{p}}) = -\ell(\boldsymbol{\beta}) $$

因此，要找到一個估計 $\hat{\boldsymbol{\beta}}$ 的最小化損失函數，也就相當於要找到對數概似函數的極大值。

$$ \begin{align*} \hat{\boldsymbol{\beta}} & = \argmin_{\boldsymbol{\beta} \in \mathbb{R}^{n + 1}} L(Y, \hat{\boldsymbol{p}}) \\ & = \argmax_{\boldsymbol{\beta} \in \mathbb{R}^{n + 1}} \left( - L(Y, \hat{\boldsymbol{p}}) \right) \\ & = \argmax_{\boldsymbol{\beta} \in \mathbb{R}^{n + 1}} \ell(\boldsymbol{\beta}) \\ & = \argmax_{\boldsymbol{\beta} \in \mathbb{R}^{n + 1}} \left( \sum_{y_i = 1} \ln(\hat{p_i}) + \sum_{y_i = 0}\ln(1 - \hat{p_i}) \right) \\ & = \argmax_{\boldsymbol{\beta} \in \mathbb{R}^{n + 1}} \left( \sum_{y_i = 1} \ln \left( \frac{\exp(X_i^\top \boldsymbol{\beta})}{1 + \exp(X_i^\top \boldsymbol{\beta})} \right) + \sum_{y_i = 0}\ln \left( \frac{1}{1 + \exp(X_i^\top \boldsymbol{\beta})} \right) \right) \end{align*} $$

欲求解 $\hat{\boldsymbol{\beta}}$ 的最佳解，我們會使用最大概似估計（maximum likelihood estimation, MLE），透過由 $\ell(\boldsymbol{\beta}) $ 對 $\boldsymbol{\beta}$ 取一階導數並設為 0 ，以尋找極點。

首先，整理一下 $\ell(\boldsymbol{\beta})$ ：

$$ \begin{align*} \ell(\boldsymbol{\beta}) & = \sum_{y_i = 1} \ln \left( \frac{\exp(X_i^\top \boldsymbol{\beta})}{1 + \exp(X_i^\top \boldsymbol{\beta})} \right) + \sum_{y_i = 0}\ln \left( \frac{1}{1 + \exp(X_i^\top \boldsymbol{\beta})} \right) \\ & = \sum_{i=1}^m \left[ y_i \ln \left( \frac{\exp(X_i^\top \boldsymbol{\beta})}{1 + \exp(X_i^\top \boldsymbol{\beta})} \right) + (1 - y_i) \ln \left( \frac{1}{1 + \exp(X_i^\top \boldsymbol{\beta})} \right) \right] \\ & = \sum_{i=1}^m \left[ y_i \ln \left( \exp(X_i^\top \boldsymbol{\beta}) \right) - y_i \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) + (1 - y_i) \ln \left(1 \right) - (1 - y_i) \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right] \\ & = \sum_{i=1}^m \left[ y_i \ln \left( \exp(X_i^\top \boldsymbol{\beta}) \right) - y_i \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) - \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) + y_i \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right] \\ & = \sum_{i=1}^m \left[ y_i \ln \left( \exp(X_i^\top \boldsymbol{\beta}) \right) - \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right] \\ & = \sum_{i=1}^m \left[ y_i X_i^\top \boldsymbol{\beta} - \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right] \\ \end{align*} $$

其一階偏導數計算如下：

$$ \begin{align*} \frac{\partial}{\partial \beta_0} \ell(\boldsymbol{\beta}) & = \frac{\partial}{\partial \beta_0} \ell(\boldsymbol{\beta}) \\ & = \frac{\partial}{\partial \beta_0} \left( \sum_{i=1}^m \left[ y_i X_i^\top \boldsymbol{\beta} - \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right] \right) \\ & = \frac{\partial}{\partial \beta_0} \left( \sum_{i=1}^m y_i X_i^\top \boldsymbol{\beta} - \sum_{i=1}^m \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right) \\ & = \sum_{i=1}^m y_i \frac{\partial}{\partial \beta_0} X_i^\top \boldsymbol{\beta} - \sum_{i=1}^m \frac{\partial}{\partial \beta_0} \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \\ & = \sum_{i=1}^m y_i - \sum_{i=1}^m \hat{p_i} \\ & = \sum_{i=1}^m (y_i - \hat{p_i}) \end{align*} $$

其中， $\frac{\partial}{\partial \beta_0} X_i^\top \boldsymbol{\beta} = 1$ ； $\frac{\partial}{\partial \beta_0} \ln(1 + \exp(X_i^\top \boldsymbol{\beta})) = \frac{\exp(X_i^\top \boldsymbol{\beta})}{1 + \exp(X_i^\top \boldsymbol{\beta})} = \sigma(X_i^\top \boldsymbol{\beta}) = \hat{p_i}$ 。

$$ \begin{align*} \frac{\partial}{\partial \beta_{j, j \neq 0}} \ell(\boldsymbol{\beta}) & = \frac{\partial}{\partial \beta_{j, j \neq 0}} \ell(\boldsymbol{\beta}) \\ & = \frac{\partial}{\partial \beta_{j, j \neq 0}} \left( \sum_{i=1}^m \left[ y_i X_i^\top \boldsymbol{\beta} - \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \right] \right) \\ & = \sum_{i=1}^m y_i \frac{\partial}{\partial \beta_{j, j \neq 0}} X_i^\top \boldsymbol{\beta} - \sum_{i=1}^m \frac{\partial}{\partial \beta_{j, j \neq 0}} \ln \left( 1 + \exp(X_i^\top \boldsymbol{\beta}) \right) \\ & = \sum_{i=1}^m y_i x_{ij} - \sum_{i=1}^m x_{ij} \hat{p_i} \\ & = \sum_{i=1}^m x_{ij} (y_i - \hat{p_i}) \end{align*} $$

其中， $\frac{\partial}{\partial \beta_{j, j \neq 0}} X_i^\top \boldsymbol{\beta} = x_{ij}$ ； $\frac{\partial}{\partial \beta_{j, j \neq 0}} \ln(1 + \exp(X_i^\top \boldsymbol{\beta})) = \frac{x_{ij} \exp(X_i^\top \boldsymbol{\beta})}{1 + \exp(X_i^\top \boldsymbol{\beta})} = x_{ij} \sigma(X_i^\top \boldsymbol{\beta}) = x_{ij} \hat{p_i}$ ； $i = 1, 2, \cdots, m$ ， $j = 0, 1, \cdots, n$ 。

將前二式合併，可以得到

$$ \frac{\partial}{\partial \beta_{j}} \ell(\boldsymbol{\beta}) = \sum_{i=1}^m x_{ij} (y_i - \hat{p_i}) $$

其中， $x_{i0} = 1$ ， $j = 0, 1, \cdots, n$ 。

假設一階偏導數為 0 ，則

$$ \begin{align*} & \frac{\partial}{\partial \beta_j} \ell(\boldsymbol{\beta}) = 0 \\ \iff & \sum_{i=1}^m x_{ij} (y_i - \hat{p_i}) = 0 \\ \end{align*} $$

至此，我們會發現邏輯迴歸無法像是線性迴歸一樣透過代數計算得到一般解。因此，我們要改換思路，使用數值方法求解。

數值方法求解

一般來說，我們會使用梯度下降法（gradient descent）最小化損失函數 $L(Y, \hat{\boldsymbol{p}}) = L(\boldsymbol{\beta})$ ，用於將 $\hat{\boldsymbol{\beta}}$ 逼近真實解 $\boldsymbol{\beta}$ 。

令梯度為

$$ \begin{align*} \nabla L(\boldsymbol{\beta}) & = \frac{\partial}{\partial \boldsymbol{\beta}} L(\boldsymbol{\beta}) \\ & = \left( \frac{\partial L}{\partial \beta_0}, \frac{\partial L}{\partial \beta_1}, \cdots, \frac{\partial L}{\partial \beta_n} \right) \end{align*} $$

在先前的計算，我們知道

$$ \frac{\partial L}{\partial \beta_j} = \frac{\partial}{\partial \beta_j} \left( -\ell(\boldsymbol{\beta}) \right) = \sum_{i=1}^m x_{ij}(\hat{p_i} - y_i) $$

因此，梯度可以表示為

$$ \nabla L(\boldsymbol{\beta}) = \boldsymbol{X}^\top (\hat{\boldsymbol{p}} - Y) \in \mathbb{R}^{n+1} $$

而更新函式如下

$$ \boldsymbol{\beta}^{(t+1)} = \boldsymbol{\beta}^{(t)} - \eta \cdot \nabla L(\boldsymbol{\beta}^{(t)}) $$

其中， $t$ 表示第 $t$ 次迭代； $\eta$ 是學習率（learning rate），控制每次更新的步長。經過多次迭代後， $\boldsymbol{\beta}^{(t)}$ 會逐步趨近於最小化損失函數的解，當 $\boldsymbol{\beta}^{(t)}$ 不再變化，或是達到迭代次數上限時，我們將其記作 $\hat{\boldsymbol{\beta}}$ ，作為模型係數的最終估計值。

預測方法

當求出 $\boldsymbol{\beta}$ 的估計值 $\hat{\boldsymbol{\beta}}$ 時，我們便可以計算預測機率 $\hat{\boldsymbol{p}} = \sigma(\boldsymbol{X}\hat{\boldsymbol{\beta}})$ ，並且透過一個門檻值（threshold）將機率值轉換為預測類別。

介於機率值落在 $[0, 1]$ 區間，通常門檻值會設定為 0.5 ，使得

$$ \begin{align*} \hat{y_i} = \left\{\begin{matrix} 1, & \text{if \ } \hat{p_i} \geq 0.5 \\ 0, & \text{if \ } \hat{p_i} < 0.5 \end{matrix}\right., && \text{where } i = 1, 2, \cdots, m \end{align*} $$

假設檢定

估計完係數 $\hat{\boldsymbol{\beta}}$ 後，我們會想知道這些變數是否對結果具有統計上的顯著影響。可以透過假設檢定（hypothesis testing）進行測試。

Wald 檢定

針對單變數假設檢定，我們可以使用 Wald 統計量進行 Wald 檢定（Wald test），其原始假設如下：

$$ \left\{\begin{align*} & H_0: \theta = \theta_0 \\ & H_a: \theta \neq \theta_0 \end{align*}\right. $$

其中， $H_0$ 代表虛無假設（null hypothesis）， $H_a$ 代表對立假設（alternative hypothesis）； $\theta$ 是要檢定的變數； $\theta_0$ 是常數。Wald 檢定可以透過 Wald 統計量 $W$ 進行檢定，當出現以下情形時，我們將拒絕 $H_0: \theta = \theta_0$ 的假設。 $$ \begin{align*} &W > z_{1 - \alpha / 2} \\ &W < z_{\alpha / 2} \\ &W^2 > \chi^2_{1, 1-\alpha} \end{align*} $$

其中， $\alpha$ 是顯著水準（significance level），且 $\alpha \in (0, 1)$ ； $z_\alpha$ 是在標準常態分佈下，落在兩側各 $\alpha$ 區域外的臨界值； $\chi^2_{k, \alpha}$ 是在自由度 $k$ 與顯著水準 $\alpha$ 下的卡方分佈。統計量 $W$ 的計算方式如下：

$$ W = \frac{\hat{\theta}_{MLE} - \theta}{s(\hat{\theta})} \sim N(0, 1) $$

其中， $\hat{\theta}_{MLE}$ 是 $\theta$ 的 MLE ； $N(0, 1)$ 是標準常態分佈（standard normal distribution）； $s(\hat{\theta})$ 是 $\hat{\theta}_{MLE}$ 的標準誤（standard error），可由其變異數估計：

$$ s^2(\hat{\theta}) = \operatorname{Var}(\hat{\theta}) \approx - \frac{1}{\ell’’(\hat{\theta})} $$

這裡的 $\ell’’ (\hat{\theta})$ 是對數概似函數 $\ell(\theta)$ 的二階導數，即費雪資訊（Fisher information, FI ，記為 $\mathcal{I}$）在估計值處的負倒數：

$$ \mathcal{I}(\hat{\theta}) = - \ell’’(\hat{\theta}) $$

因此， $s^2(\hat{\theta})$ 也可記為

$$ s^2(\hat{\theta}) = \frac{1}{\mathcal{I}(\hat{\theta})} $$

標準誤可由以下估計

$$ s(\hat{\theta}) = \sqrt{\frac{1}{\mathcal{I}(\hat{\theta})}} = \sqrt{- \frac{1}{\ell’’(\hat{\theta})}} $$

單變數假設檢定

我們針對第 $j$ 個變數進行如下的假設檢定：

$$ \left\{\begin{align*} & H_0: \beta_j = 0 \\ & H_a: \beta_j \neq 0 \end{align*}\right. $$

其中， $j = 0, 1, \cdots, n$ 。此假設用於檢定第 $j$ 個變數是否對預測目標有顯著影響，我們可以透過 Wald 統計量進行檢定。

令 $\hat{\boldsymbol{\beta}}$ 是 $\boldsymbol{\beta}$ 的 MLE ，則根據漸近常態分佈

$$ \hat{\boldsymbol{\beta}} - \boldsymbol{\beta} \sim N(0, s^2(\hat{\boldsymbol{\beta}})) $$

因此，可定義 Wald 統計量如下：

$$ W = \frac{\hat{\beta}_j}{s(\hat{\beta}_j)} $$

其中，$s(\hat{\beta}_j)$ 為估計值 $\hat{\beta}_j$ 的標準誤。根據漸近性質，$W$ 近似服從標準常態分布 $N(0, 1)$。

當我們設定顯著水準 $\alpha$ ，可根據雙尾檢定，在下列情況拒絕虛無假設 $H_0$：

$$ |W| > z_{1 - \alpha / 2} $$

也可以平方後使用卡方分布進行檢定：

$$ W^2 > \chi^2_{1, 1-\alpha} $$

若拒絕 $H_0$，表示第 $j$ 個變數對目標變數具有統計上顯著的影響，否則則無顯著證據顯示該變數重要。

多變數假設檢定

我們常用對數概似比檢定（Likelihood Ratio Test, LRT）用於檢定多個變數是否對模型有顯著影響，其原理為比較兩個模型的對數概似函數值。 LRT 的假設如下：

$$ \left\{\begin{align*} & H_0: \beta_1 = \beta_2 = \cdots = \beta_n = 0 \\ & H_a: \text{至少一個 } \beta_j \neq 0 \end{align*}\right. $$

其虛無假設為簡化模型（reduced model），表示所有自變數皆不影響目標變數；而對立假設則是完整模型（full model），表示至少存在一個自變數具有顯著影響。

其檢定統計量定義為：

$$ \Lambda = -2 \left[ \ell(\boldsymbol{\beta}_{\text{reduced}}) - \ell(\boldsymbol{\beta}_{\text{full}}) \right] $$

其中 $\ell(\hat{\boldsymbol{\beta}}_{\text{reduced}})$ 是簡化模型的對數概似函數； $\ell(\hat{\boldsymbol{\beta}}_{\text{full}})$ 是完整模型的對數概似函數； $\Lambda$ 為對數概似比統計量（likelihood ratio statistic）。

在虛無假設 $H_0$ 成立下，$\Lambda$ 服從自由度為 $q$ 的卡方分布（$\chi^2_q$）。

當出現以下情況時，拒絕虛無假設 $H_0$：

$$ \Lambda > \chi^2_{q, 1 - \alpha} $$

其中 $\alpha$ 為顯著水準。

信賴區間

對每一個係數 $\beta_j$，我們可以建構 $(1 - \alpha)$% 的信賴區間，其形式為：

$$ [\hat{\beta}_j \pm z_{\alpha/2} \cdot s(\hat{\beta}_j)] $$

其中 $\hat{\beta}_j$ 是估計係數； $z_{\alpha/2}$ 是在標準常態分佈下，落在兩側各 $\frac{\alpha}{2}$ 區域外的臨界值； $\alpha$ 為顯著水準；$s(\hat{\beta}_j)$ 為 $\hat{\beta}_j$ 的標準誤。

此信賴區間可解釋為：在多次重複抽樣下，有 $(1 - \alpha)$% 的機會包含真實的參數 $\beta_j$。若此信賴區間包含 0，則代表在給定的顯著水準下，我們無法拒絕虛無假設 $\beta_j = 0$，變數可能對結果沒有顯著影響。

若我們希望以勝算比來解釋變數的影響，則對應的估計量為：

$$ \widehat{\text{OR}}_j = \exp(\hat{\beta}_j) $$

表示自變數向量 $(x_{1j}, x_{2j}, \cdots, x_{mj})$ 每增加一單位時，事件發生的勝算變化倍率。其 $(1 - \alpha)$% 的信賴區間為：

$$ \left[ \exp\left(\hat{\beta}_j - z_{\alpha/2} \cdot s(\hat{\beta}_j)\right), \exp\left(\hat{\beta}_j + z_{\alpha/2} \cdot s(\hat{\beta}_j)\right) \right] $$

此信賴區間可解釋為：在多次重複抽樣下，有 $(1 - \alpha)%$ 的機會包含真實的勝算比 $\text{OR}_j$。若信賴區間包含 1，則表示變數對應的影響在統計上可能不顯著，因為 $\exp(0) = 1$ 代表沒有影響。

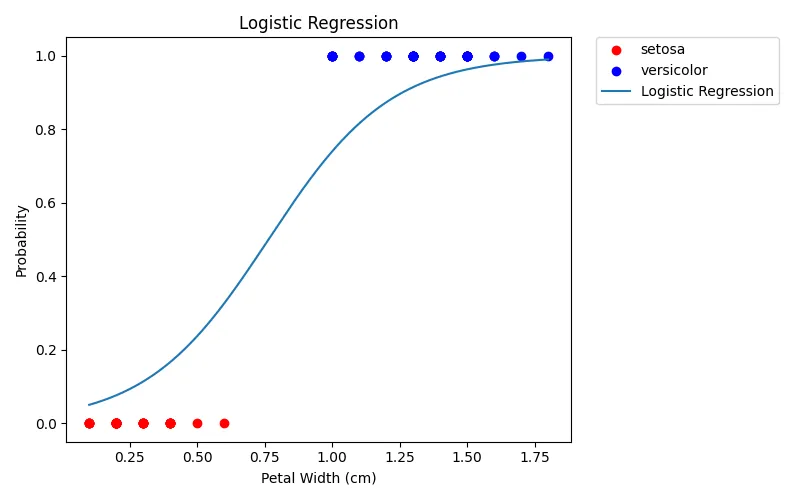
Python 範例

以下以 Iris 資料集為例，使用花瓣寬度（petal width）作為特徵，分類山鳶尾花（setosa）與變色鳶尾花（versicolor）。

首先，載入會使用到的模組。

1
2
3
4
5
6
7
8

# import modules
import numpy as np
import matplotlib.pyplot as plt
import os
from sklearn.datasets import load_iris
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.metrics import confusion_matrix, accuracy_score
import scipy.stats

讀取 Iris 資料集。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

# Iris data
iris = load_iris()  # load data
X = iris.data[:, 3:]  # data
y = iris.target  # target
class_names = iris.target_names  # Iris class names

mask = np.isin(iris.target, [0, 1])
X = X[mask]
y = y[mask]
class_names = class_names[0:2]

print(f'\nclass names: \n{class_names}')
print(f'\nfeature names: \n{iris.feature_names[3:]}')

1
2
3
4
5

class names: 
['setosa' 'versicolor']

feature names: 
['petal width (cm)']

設定圖片路徑。

1
2
3

# configs
output_dir = 'plots'  # output directory
os.makedirs(output_dir, exist_ok=True)

進行邏輯迴歸，並畫圖。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# logistic regression
log_reg = LogisticRegression()
log_reg.fit(X, y)
y_log_prob = log_reg.predict_proba(x_test)[:, 1]

plt.figure(figsize=(8, 5))
plt.scatter(X[y == 0], y[y == 0], color='red', label=class_names[0])
plt.scatter(X[y == 1], y[y == 1], color='blue', label=class_names[1])
plt.plot(x_test, y_log_prob, label='Logistic Regression')
plt.xlabel('Petal Width (cm)')
plt.ylabel('Probability')
plt.title('Logistic Regression')
plt.legend(loc='upper left', bbox_to_anchor=(1.05, 1.0), borderaxespad=0)
plt.tight_layout()
plt.savefig(os.path.join(output_dir, 'logistic.webp'))
plt.show()
plt.close()

迴歸係數 $\boldsymbol{\beta}$ 如下，因為只有使用一個自變數，因此只會有截距項（intercept）$\beta_0$ 和係數 $\beta_1$ 。

1
2
3
4

# logistic regression coefficients
coef = log_reg.coef_[0][0]
intercept = log_reg.intercept_[0]
print(f'\nCoefficients:\nintercept = {intercept:.4f}\ncoef = {coef:.4f}')

1
2
3

Coefficients:
intercept = -3.3799
coef = 4.4240

以下為各係數標準誤、 p-value 和 95% 信賴區間。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# logistic regression summary
X_design = np.hstack([np.ones((X.shape[0], 1)), X])
p = log_reg.predict_proba(X)[:, 1]
W = np.diag(p * (1 - p))
Fisher_inv = np.linalg.inv(X_design.T @ W @ X_design)
se = np.sqrt(np.diag(Fisher_inv))

z = np.array([intercept, coef]) / se
p_values = 2 * (1 - scipy.stats.norm.cdf(np.abs(z)))
ci_95 = np.array([
    [intercept, coef] - 1.96 * se,
    [intercept, coef] + 1.96 * se
]).T

print("\nSummary of Logistic Regression Coefficients:")
for i, name in enumerate(['intercept', 'petal width']):
    print(f"{name:12s}: coef = {intercept if i==0 else coef:.4f} | SE = {se[i]:.4f} | p = {p_values[i]} | 95% CI = [{ci_95[i,0]:.4f}, {ci_95[i,1]:.4f}]")

1
2
3

Summary of Logistic Regression Coefficients:
intercept   : coef = -3.3799 | SE = 0.6242 | p = 6.140579889013509e-08 | 95% CI = [-4.6034, -2.1565]
petal width : coef = 4.4240 | SE = 0.7091 | p = 4.40006697743911e-10 | 95% CI = [3.0342, 5.8138]

以下是混淆矩陣與準確率。

1
2
3
4
5
6

# confusion matrix and accuracy
y_log_pred = log_reg.predict(X)
cm = confusion_matrix(y, y_log_pred)
acc = accuracy_score(y, y_log_pred)
print(f'\nConfusion Matrix:\n{cm}')
print(f'\nAccuracy: {acc}')

1
2
3
4
5

Confusion Matrix:
[[50  0]
 [ 0 50]]

Accuracy: 1.0

結語

邏輯迴歸是一種簡單實用的二元分類模型，能夠透過少許的計算，快速完成二元類別的判斷。然而，它也有一些限制，例如假設自變數與對數勝算之間存在線性關係，且各觀測值彼此獨立。因此，在使用邏輯迴歸時，應配合模型診斷與適當的資料前處理，以確保分析結果的可信度。

作為經典的基礎分類模型，邏輯迴歸不僅在統計推論中佔有重要地位，也常被用於機器學習的初步建模與特徵選擇，是受資料分析者喜愛的重要工具之一。

延伸學習

• 本文使用的 GitHub 儲存庫。

參考資料

• 最小平方法。（2025年7月4日）。維基百科，自由的百科全書。2025年7月25日參考自 https://zh.wikipedia.org/wiki/最小二乘法

• 線性迴歸。（2025年7月5日）。維基百科，自由的百科全書。2025年7月25日參考自 https://zh.wikipedia.org/zh-tw/線性回歸

• 邏輯迴歸。（2024年11月15日）。維基百科，自由的百科全書。2025年7月25日參考自 https://zh.wikipedia.org/zh-tw/邏輯斯諦迴歸

• Logistic regression。（2025年7月24日）。維基百科，自由的百科全書。2025年7月25日參考自 https://en.wikipedia.org/wiki/Logistic_regression

• Cross-entropy。（2025年7月22日）。維基百科，自由的百科全書。2025年7月25日參考自 https://en.wikipedia.org/wiki/Cross-entropy

• S型函數。（2023年9月23日）。維基百科，自由的百科全書。2025年7月25日參考自 https://zh.wikipedia.org/zh-tw/S型函数

• Logit。（2025年7月20日）。維基百科，自由的百科全書。2025年7月25日參考自 https://en.wikipedia.org/wiki/Logit

• 邏輯斯迴歸 (Logistic Regression) 之勝算比 (Odds Ratio) 告訴您什麼資訊？。（無日期）。Minitab。2025年7月25日參考自 https://www.sfi-minitab.com.tw/support/faq.php?fid=55

• Logit transform。（無日期）。STATSREF。2025年7月25日參考自 https://www.statsref.com/HTML/logit.html

• How do you fit a model when the dependent variable is a proportion?。（無日期）。STATA。2025年7月25日參考自 https://www.stata.com/support/faqs/statistics/logit-transformation/

• 【羅吉斯迴歸分析(Logistic regression, logit model)-統計說明與SPSS操作】。（2017年7月8日）。永析統計及論文諮詢顧問。2025年7月25日參考自 https://www.yongxi-stat.com/logistic-regression/

• 伯努利分布。（2025年7月3日）。維基百科，自由的百科全書。2025年7月25日參考自 https://zh.wikipedia.org/zh-tw/伯努利分布

• 王超辰。（無日期）。第 16 章 假設檢驗的近似方法。醫學統計學。2025年7月25日參考自 https://bookdown.org/ccwang/medical_statistics6/section-16.html