交叉驗證的方法
封面圖片是由 ChatGPT 生成的交叉驗證的圖片,使用的提示詞為 “A 2D vector graphic visually representing cross-validation in machine learning, with a light blue background. Include a clear title “CROSS-VALIDATION” at the top. Show a dataset divided into five folds labeled “Fold 1” to “Fold 5”. Use arrows to indicate training and validation data splits, and include labeled boxes for “Training Data”, “Validation Data”, and “Model”. Use clean lines, modern flat design, and contrasting colors for clarity. Aspect ratio 16:9.” 。
前言
交叉驗證(Cross-Validation, CV)是常用於機器學習的模型驗證技術,用於評估模型在未見資料上的泛化能力。透過將資料集切分為訓練集、驗證集與測試集,並反覆進行訓練與評估,交叉驗證能在資料量有限的情況下,有效測試模型的性能,評估模型的泛化能力並用於減少過擬合和與偏差等問題。
交叉驗證在控制過擬合、選擇最佳模型、調整超參數等方面扮演重要角色,特別是能預測模型面對新資料的表現,是現代機器學習流程中不可或缺的一環。
模型泛化
模型泛化(model generalization)是指模型在面對未曾見過的新資料時,仍能保持良好預測表現的能力。換句話說,一個具備良好泛化能力的模型,不僅在訓練資料上表現優異,也能有效應用於真實世界的全新數據。
當訓練一個模型時,若這個模型只記住了訓練資料的細節,而無法應用於新資料,那麼這個模型就產生了過擬合(Overfitting)。這類模型雖然在訓練階段表現出色,但在實際應用中常常表現不佳。
與此相對,一個具備良好泛化能力的模型,能夠將學到的知識應用於全新的資料上,依然維持穩定且準確的預測表現。這類模型並非僅僅記住訓練資料的特徵,更是成功掌握資料中隱含的規律與模式。具備泛化能力的模型在真實應用場景中更具實用性,無論資料來源如何變動,都能持續做出可靠的決策或預測。
相關字詞
過擬合(Overfitting):模型對訓練資料過度學習,失去對新資料的預測能力。
欠擬合(Underfitting):模型學得不夠,即使是訓練資料也無法表現良好。
資料集分割
一般進行模型訓練時,我們通常會將資料集拆分為訓練集(training set)與測試集(test set),其中在訓練階段模型只會對訓練集進行擬合,而測試集的資料並未參與訓練,因此測試集可以拿來當作最終評估模型的好壞。但是在模型訓練中,我們可能有一些參數需要在訓練時進行最佳化,這時候我們可以從訓練集中再拆分一份資料作為驗證集(validation set),使得驗證集的表現是最佳的,用於找出最佳的模型參數。為了避免模型對驗證集過擬合,我們可以使用交叉驗證對訓練資料進行分組,並且每次取不同的部分子集訓練模型,部分子集評估模型,重複這個過程增加模型的泛化能力。
常見的交叉驗證方法
| 方法名稱 | 說明 | 適用情境 / 優點 |
|---|---|---|
| 留出法 | 將資料隨機切分為訓練集與測試集,僅進行一次訓練與評估。 | 快速簡便,適合初步測試。資料量足夠時表現穩定。 |
| K 折交叉驗證 | 將資料平均切為 K 個子集,進行 K 次訓練與測試,最後平均結果。 | 常見且穩定,適合一般性模型評估。 |
| 分層 K 折交叉驗證 | 在 K 折交叉驗證的基礎上,保留各類別在每個子集中的比例。 | 適用於分類問題,尤其是類別不平衡的資料集。 |
| 留一交叉驗證 | 每次僅留一筆樣本做為驗證,其餘樣本用於訓練。總共進行 N 次。 | 適用於樣本數極少的情況,但計算成本高。 |
| 留 P 交叉驗證 | 每次留 $p$ 筆樣本驗證,其餘訓練,遍歷所有可能的 $p$ 組合。 | 提供最完整的泛化測試,但計算非常耗時。 |
| 重複 K 折交叉驗證 | 對 K 折交叉驗證流程進行多次隨機切分與重複驗證。 | 提升穩定性與可靠性,減少隨機切分的偏差。 |
| 分組 K 折交叉驗證 | 切分時確保同一群組資料不會同時出現在訓練與測試集中。 | 適用於有群組性質的資料,避免資訊洩漏。 |
| 巢狀交叉驗證 | 外層用於模型評估,內層用於超參數調整,避免過度擬合。 | 適用於需要調參的情境,提供更可靠的泛化能力評估。 |
| 蒙地卡羅交叉驗證 | 隨機多次切分資料為訓練集與測試集,評估結果取平均。 | 彈性高、實作簡單,適合資料量大時快速評估模型穩定性。 |
| 時間序列交叉驗證 | 依時間順序逐步擴展訓練集,測試集為後續時間點。 | 適用於時間序列資料,避免未來資訊外洩,維持時間因果性。 |
留出法
留出法(Hold-out Method),也有人稱作簡單交叉驗證,是最簡單的驗證方法,但是因為此方法未交叉,因此它不屬於交叉驗證的範疇。
作法
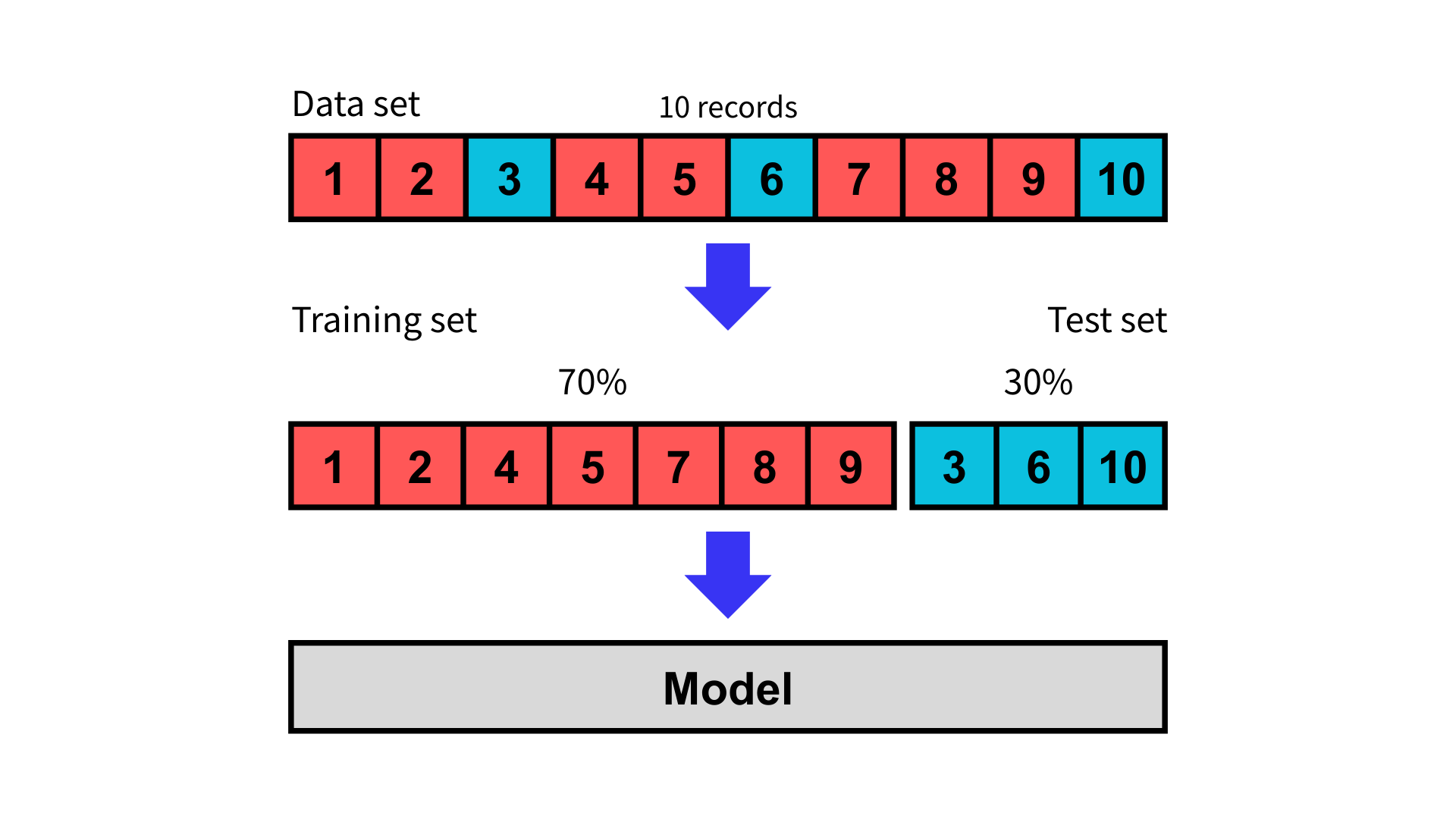
在這種方法中,我們從資料集中隨機抽取一定比例的資料作為訓練集,其餘的部分作為測試集。常見的比例有 70% 作為訓練集,30% 作為測試集,或者 90% 作為訓練集,10% 作為測試集等。然而,這種方法也存在一定的缺點,例如:
因此,在使用留出法進行模型驗證時,我們必須確保訓練資料集的數量足夠大且具多樣性,以避免評估結果失真。一般來說,測試集的比例應該控制在原始資料集的三分之一以內。
拆分訓練集與測試集後,使用訓練集訓練模型,並使用測試集進行預測,最後使用合適的評估指標評估模型。
優點
- 簡單、計算成本低,非常適合資料量極大、只需快速估計的情況。
缺點
- 結果高度依賴於一次隨機分割,評估指標不穩定且可能有偏誤。若資料量有限,可能會出現代表性不足的問題。
適用情境
- 資料量龐大時的臨時評估,或是可重複計算多次並平均結果。
K 折交叉驗證
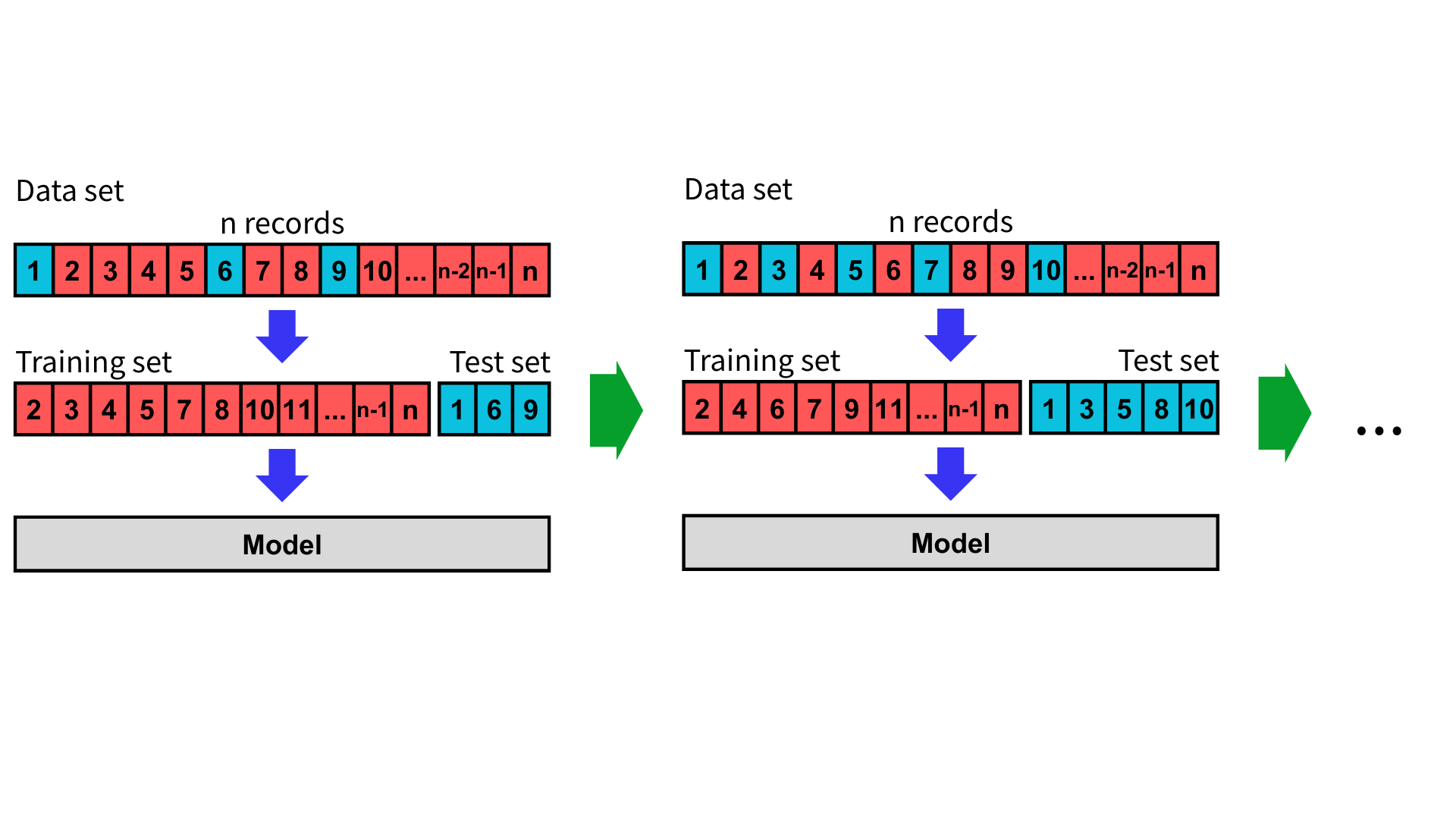
K 折交叉驗證(K-fold Cross-Validation, KCV)改進了留出方法,它能夠有效減少模型對訓練集與測試集隨機分割的依賴,並且為模型提供更穩定的評估。
作法
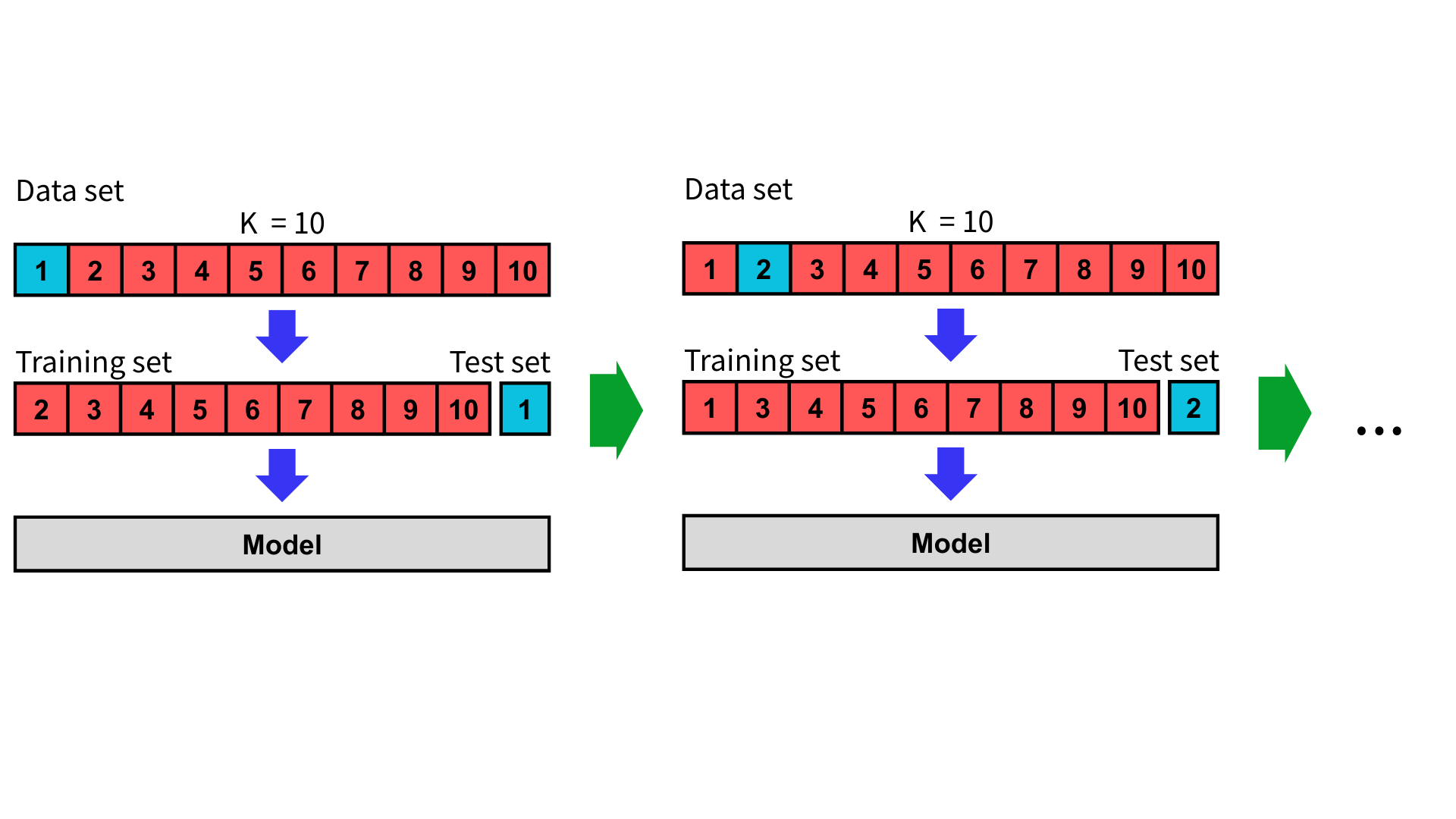
首先,K 折交叉驗證將整個數據集隨機分成 K 個大小相同的子集(folds ,又稱為折),每個子集將包含資料集中的一部分數據,並確保所有樣本都有機會出現在訓練集和測試集中。在每一次驗證中,選取其中一個子集作為測試集,其餘 K-1 個子集合併作為訓練集。同時重複這個過程 K 次,每次更換不同的子集作為測試集。
在 K 次測試後,我們會得到 K 次測試的結果,計算這些評估指標取並平均值與標準差,可以用於更準確衡量模型的泛化能力。
優點
- 每個樣本都至少一次出現在訓練集與測試集中,有效減少模型對特定劃分方式的依賴,減少偏差與過擬合風險。
- 結果更穩定,避免單次測試結果可能帶來的偏差。
- 可最大化資料利用效率,適合樣本量不足的小型資料集。
- 常見設置為 $K = 5$ 或 $K = 10$,能在模型偏差(Bias)與變異數(Variance)間取得較佳平衡。
缺點
- 需進行 K 次模型訓練,對於大型資料集可能造成負擔。
- 若切分不夠隨機,仍可能產生偏差。
- K 值太大雖精確但訓練次數過多,計算量劇增,且可能使訓練的模型過於相似,造成變異數變大。
適用情境
- 小型資料集。
- 需要客觀評估模型泛化能力的情況。
分層 K 折交叉驗證
分層 K 折交叉驗證(Stratified K-fold Cross-Validation, SKCV)是 K 折交叉驗證的改進方法。因為 K 折交叉驗證是將資料集進行隨機拆分,所以可能會造成以下情況。
因為拆分資料集的過程剛好把類別都分開了,個別模型在訓練時無法抓取到測試集中的分類特徵,這可能導致在訓練模型時出現偏差。
作法
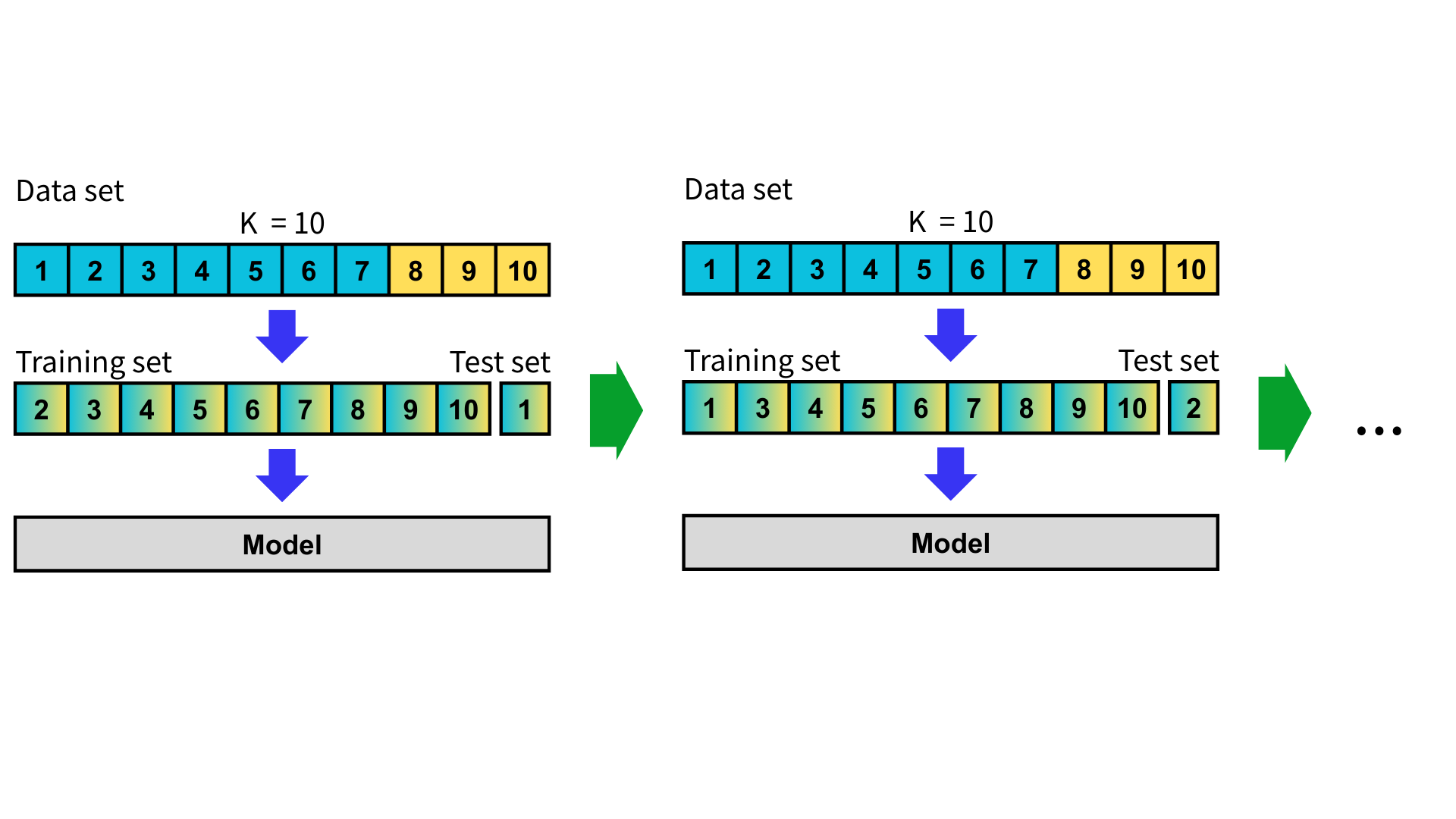
首先,取得各類別在母體樣本中的比例,在拆分子集時考慮各類別的比例,使得每一個子集對於不同類別的成分占比相近。
接下來操作與 K 折交叉驗證相同,在每一次驗證中,選取其中一個子集作為測試集,其餘 K-1 個子集合併作為訓練集。同時重複這個過程 K 次,每次更換不同的子集作為測試集。
在 K 次測試後,計算這些評估指標並取平均值與標準差,就可以更準確衡量模型的泛化能力。
優點
- 避免資料切分造成類別不平衡。
- 能更準確反映模型在真實資料中處理不同類別的表現,特別是在類別分布極不均的情況下。
- 增加評估結果的穩定性與可信度。
缺點
- 僅適用於有標籤或類別屬性的監督式學習問題。
- 當資料量非常少或某些類別樣本過少時,仍可能在某些折中無法包含所有類別,導致評估失真。
- 相較於簡單隨機拆分,實作上稍微複雜,計算時間增加,對於大型資料集可能造成負擔。
適用情境
- 二元或多元分類問題且類別不平衡的資料集,如醫療診斷(疾病與否)、欺詐檢測、少數類別偵測等。
- 模型評估時要求更穩定、公平的比較。
- 資料集中某些類別樣本佔比非常小的情況。
留一交叉驗證
留一交叉驗證(Leave-One-Out Cross-Validation, LOOCV)是一種特殊形式的 K 折交叉驗證,其中特殊之處在於每次僅從資料集中選出一筆作為測試集,其餘所有資料皆作為訓練集。若資料集包含 $n$ 筆資料,則會進行 $n$ 次訓練與驗證。由於每筆資料都曾被用作一次測試,留一交叉驗證能夠充分利用每一筆資料,對模型的泛化能力更精細的評估。
作法
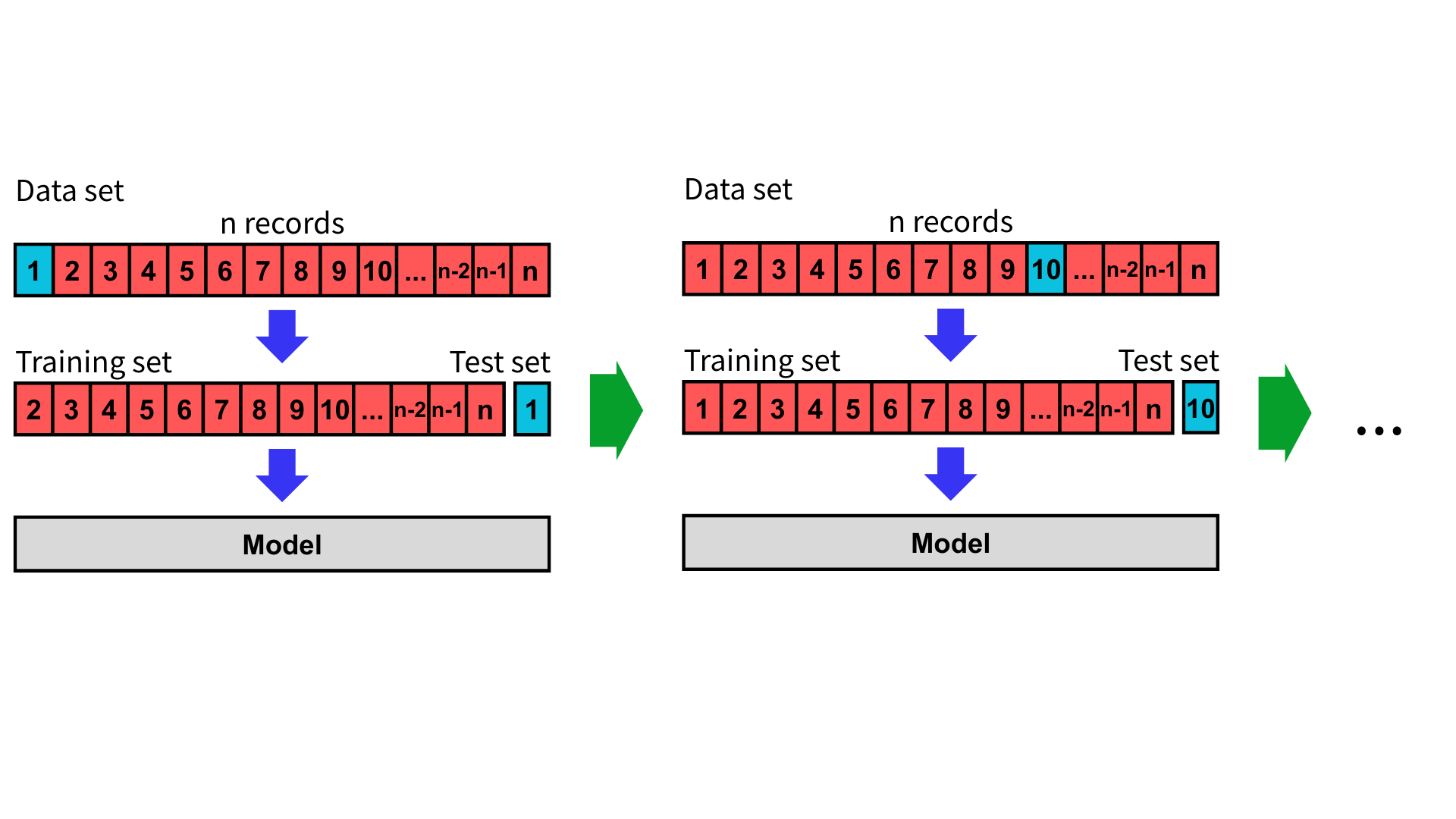
假設資料集中有 $n$ 筆資料,我們從中選出一筆當測試集,其餘 $n - 1$ 筆資料作為訓練集。每次選擇不同的測試集,並重複進行 $n$ 次訓練與驗證。
將進行 $n$ 次模型訓練的評估指標取平均值與標準差,可以取得比 K 折交叉驗證更穩定、更小的估計偏差。
優點
- 最大化利用資料集。
- 不需隨機拆分資料,結果不受資料分割方式影響。
- 相對於 K 折交叉驗證,留一交叉驗證的估計偏差通常更小。
缺點
- 由於每筆資料都要重新訓練模型,因此計算成本高昂,不適合用於大型資料集。
適用情境
- 小型資料集。
- 需要精確評估模型的情況,如學術研究、實驗場域等。
留 P 交叉驗證
留 P 交叉驗證(Leave-P-Out Cross-Validation, LPOCV)是留一交叉驗證的一種推廣。與留一交叉驗證每次僅使用一筆資料作為測試集不同,留 P 交叉驗證每次從資料集中選出 $p$ 筆資料作為測試集,其餘 $n - p$ 筆作為訓練集。當 $p = 1$ 時,即為留一交叉驗證。
作法
假設資料集中有 $n$ 筆資料,我們從中選出 $p$ 筆當測試集,其餘 $n - p$ 筆資料作為訓練集。每次選擇不同的測試集,並重複進行幾次訓練與驗證。
完成模型訓練後,將評估指標取平均值與標準差,即可衡量模型的泛化能力。
理論上留 P 交叉驗證會進行 $\frac{n!}{(n - p)! p!}$ 次,在 $p = 1$ 時會是 $n$ 次,但在 $p > 1$ 時會導致要訓練的模型過多,變得不可行。因此,在實際應用中通常會採用隨機重複抽樣,以減少訓練次數,同時確保每筆資料都有機會多次作為測試集。
優點
- 可依據資料大小與需求選擇不同的 $p$ 值,平衡訓練資料量與測試資料量。
- 透過大量不同資料子集的測試,能更準確地估計模型的泛化能力。
- 遍歷並使模型訓練完所有組合的可能性,能對模型的泛化能力提供幾乎無偏估計。
缺點
- 當 $p > 1$ 且資料量大時,所有可能的組合數會急速上升,導致訓練次數過多、無法訓練完,使計算成本過於高昂。
- 實務上無法嘗試所有組合,通常只能隨機抽樣部分組合,影響穩定性與再現性。
- 多次包含相同資料點可能導致驗證誤差非獨立,影響統計推論。
適用情境
- 小型資料集。
- 需要觀察模型在不同資料組合下的穩定性時。
- 資料稀少但分析精度要求高的情況,如醫療、生物統計、心理學等領域。
重複 K 折交叉驗證
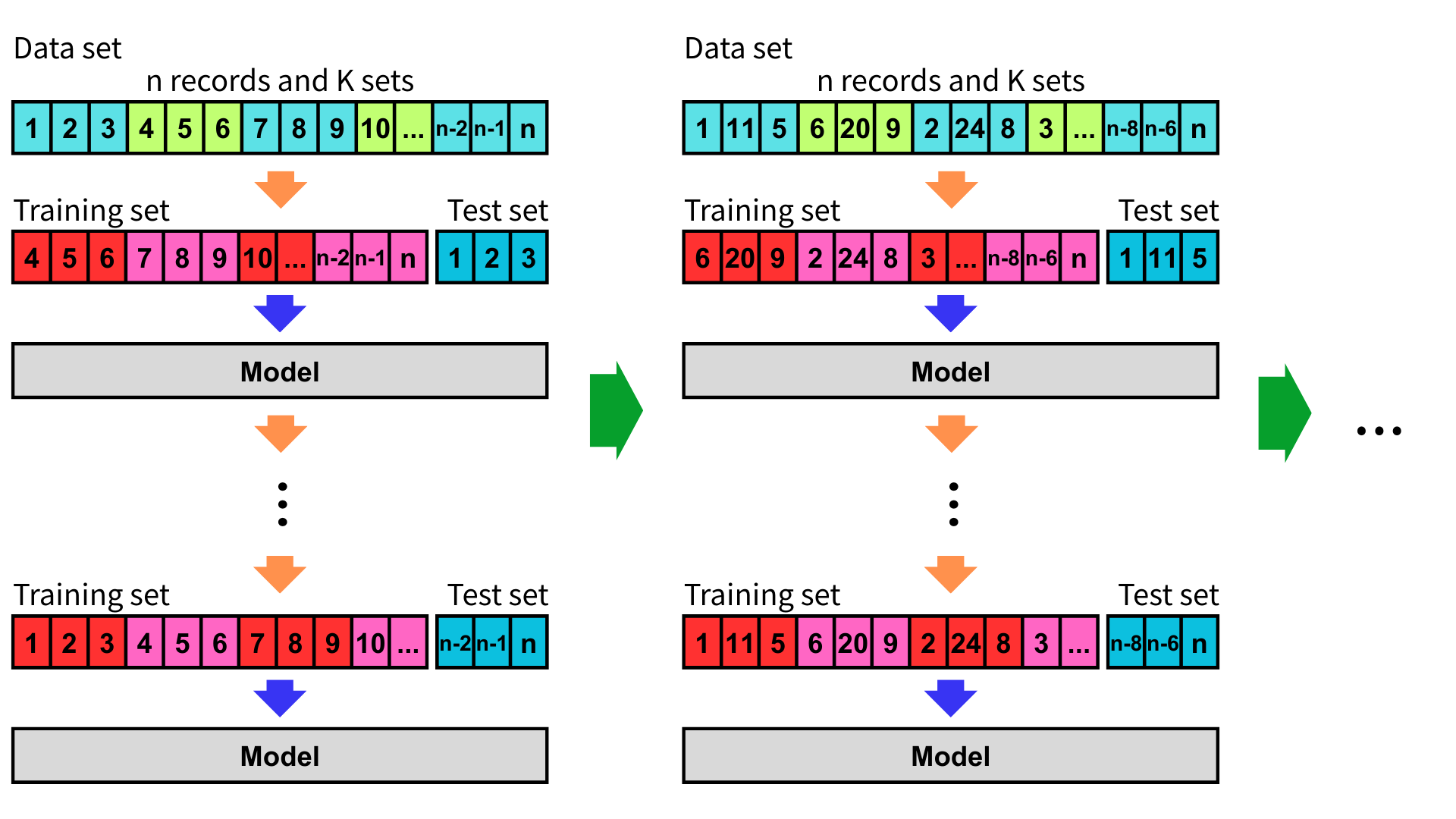
重複 K 折交叉驗證(Repeated K-fold Cross-Validation, RKCV),是 K 折交叉驗證的一種變體,其目的是將 K 折交叉驗證重複進行多次,從而提高模型評估的穩定性和準確性,並減少由於資料隨機分割帶來的波動性。
作法
如同 K 折交叉驗證的作法,將資料集隨機分成 K 個子集,取其中一個子集作為測試集,其餘 K-1 個子集合併作為訓練集,而後重複這個過程 K 次,每次更換不同的子集作為測試集。
當完成一輪 K 折交叉驗證後,將資料集重新隨機分割成 K 個子集,再次進行 K 折交叉驗證,並重複多輪 K 折交叉驗證。如果資料集較小,可能會選擇較多的重複次數,以提高模型評估的穩定性。通常會重複 5 至 10 次。
最後,對每次重複的 K 折交叉驗證結果進行評估,將評估指標平均值與標準差後即可估計模型的泛化能力。
優點
- 透過多次重複測試,可以減少由單次資料分割引起的誤差波動,提高評估結果的穩定性。
- 多次隨機重複能夠讓模型在不同的資料子集上進行測試,更全面地反映模型的泛化能力。
- 減少過擬合風險。
缺點
- 重複多次 K 折交叉驗證會增加訓練次數,使得計算成本高昂。
- 每次重複都會進行 K 次訓練和測試,顯著增加訓練時間。
- 每次重複會有不同的測試集分割,可能需要更精細的結果分析。
適用情境
- 小型資料集。
- 資料集的分佈變化較大。
分組 K 折交叉驗證
當資料中存在「群組(Group)」的關係時,例如同一使用者、病患、設備或同一段時間內的記錄,若直接對單筆資料做 K 折交叉驗證,可能會導致相同群組的資料同時出現在訓練集與測試集中,造成資料洩漏(Data Leakage),高估模型表現。
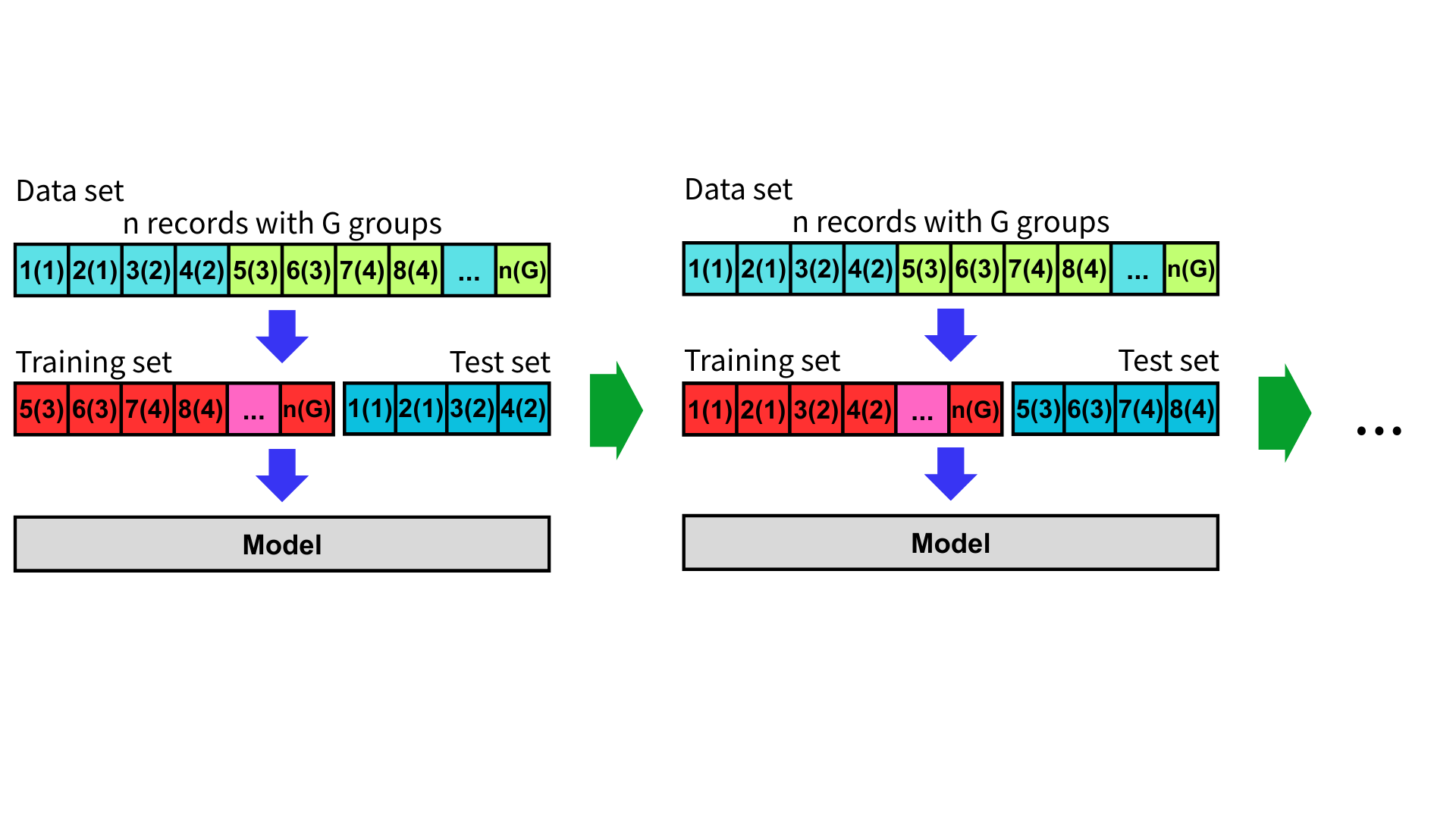
因此,衍伸了分組 K 折交叉驗證(Group K-fold Cross-Validation, GKCV)這個方法,其目的在於確保測試集中不包含出現在訓練集中的任何群組、減少模型過度擬合的風險、防止測試集過於集中在某些連續資料區段,導致評估偏差,並提升模型在「未見群組」的泛化能力。
假設有三個資料類別,每次測試集將從三個不同的群組中隨機抽樣,並確保每一輪交叉驗證中這些群組彼此不重複。
作法
首先,指定每筆資料所屬的群組,例如使用者 ID、設備編號、相同學校等。
接下來,將資料集依據群組拆分,把資料集分為多個群組。
再來,將資料集分成 K 個子集,每一個子集都由多個群組構成,確保不同子集間的群組不重複。
選取其中一個子集作為測試集,其餘 K-1 個子集合併作為訓練集。同時重複這個過程 K 次,每次更換不同的子集作為測試集。
在 K 次測試後,計算評估指標並取平均值與標準差,就可以更準確衡量模型的泛化能力。
優點
- 有效防止群組間的資料洩漏。
- 提高模型對未見資料的泛化能力。
- 測試集具有代表性,涵蓋資料的多樣性與分布。
缺點
- 群組數不足時,無法進行有效的多折交叉驗證。
- 若群組大小不均,可能導致部分子集資料量過多或過少。
- 相較於 K 折交叉驗證稍微複雜,需明確標註每筆資料的群組。
適用情境
- 任何具有群組關係且可能導致資料洩漏的情況。
巢狀交叉驗證
巢狀交叉驗證(Nested Cross-Validation, Nested CV),又稱為嵌套交叉驗證,是 K 折交叉驗證的一種變體。為了避免在同一組測試集上同時調參與評估模型,導致高估模型表現,巢狀交叉驗證應運而生。
巢狀交叉驗證透過雙層交叉驗證的方式,區分超參數選擇和測試集,避免資料洩漏,使評估模型更加可靠。
作法
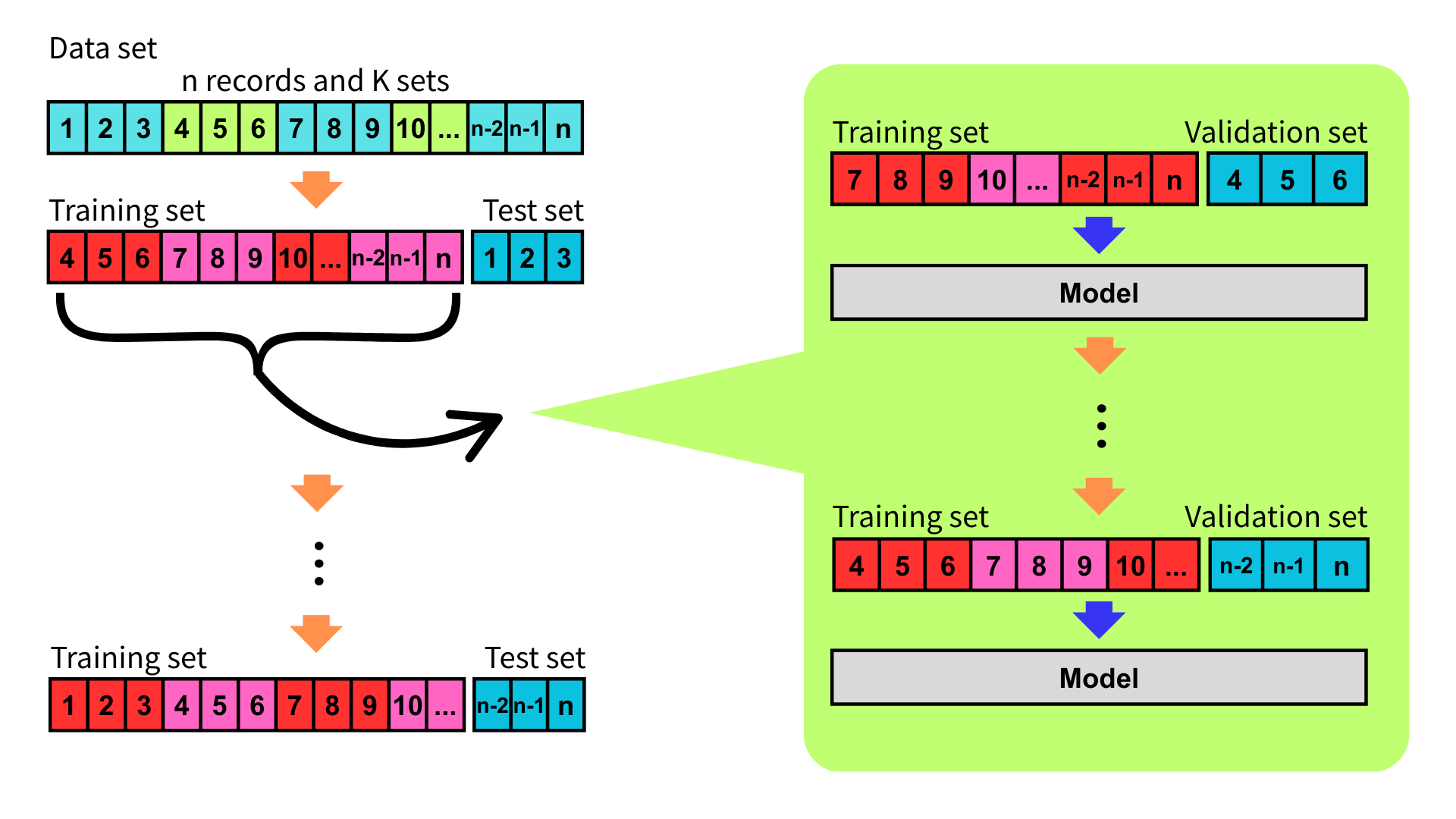
巢狀交叉驗證分為外層迴圈(Outer Loop)和內層迴圈(Inner Loop)。其中,外層迴圈用於評估模型,內層迴圈用於選擇最佳超參數。
進行巢狀交叉驗證時,首先定義外層迴圈。外層迴圈與 K 折交叉驗證相同,將資料集分成 K 個子集,每次取一子集作為測試集,其餘 K-1 個子集合併作為訓練集。
接下來定義內層迴圈,內層迴圈是將外層迴圈每一次的訓練集使用任意的交叉驗證的方法,例如再次進行 K 折交叉驗證,再重新拆分為訓練集與驗證集,並逐步對每組超參數組合進行調整與評估。
在每一次的外層迴圈中,選出在內層表現最好的超參數,並用這組超參數在外層的訓練資料上重新訓練模型,並使用測試集進行測試。
重複直到執行完外層的 K 個子集後,將評估指標取平均值與標準差,即可有效估計模型的泛化能力。
優點
- 避免資料洩漏,導致模型評估失準。
- 提高模型對未見資料的泛化能力。
- 確保選擇超參數的過程與測試資料無關,能夠客觀地選擇最佳的超參數。
缺點
- 內外雙層交叉驗證需要大量的模型訓練,使計算成本高昂。
- 需要清楚劃分外層與內層資料與邏輯。
- 不適合需要及時評估模型狀況的情況。
- 不適合大型資料集。
適用情境
- 需要精確尋找模型超參數的情況。
- 容易發生過擬合或資料洩漏的資料集。
蒙地卡羅交叉驗證
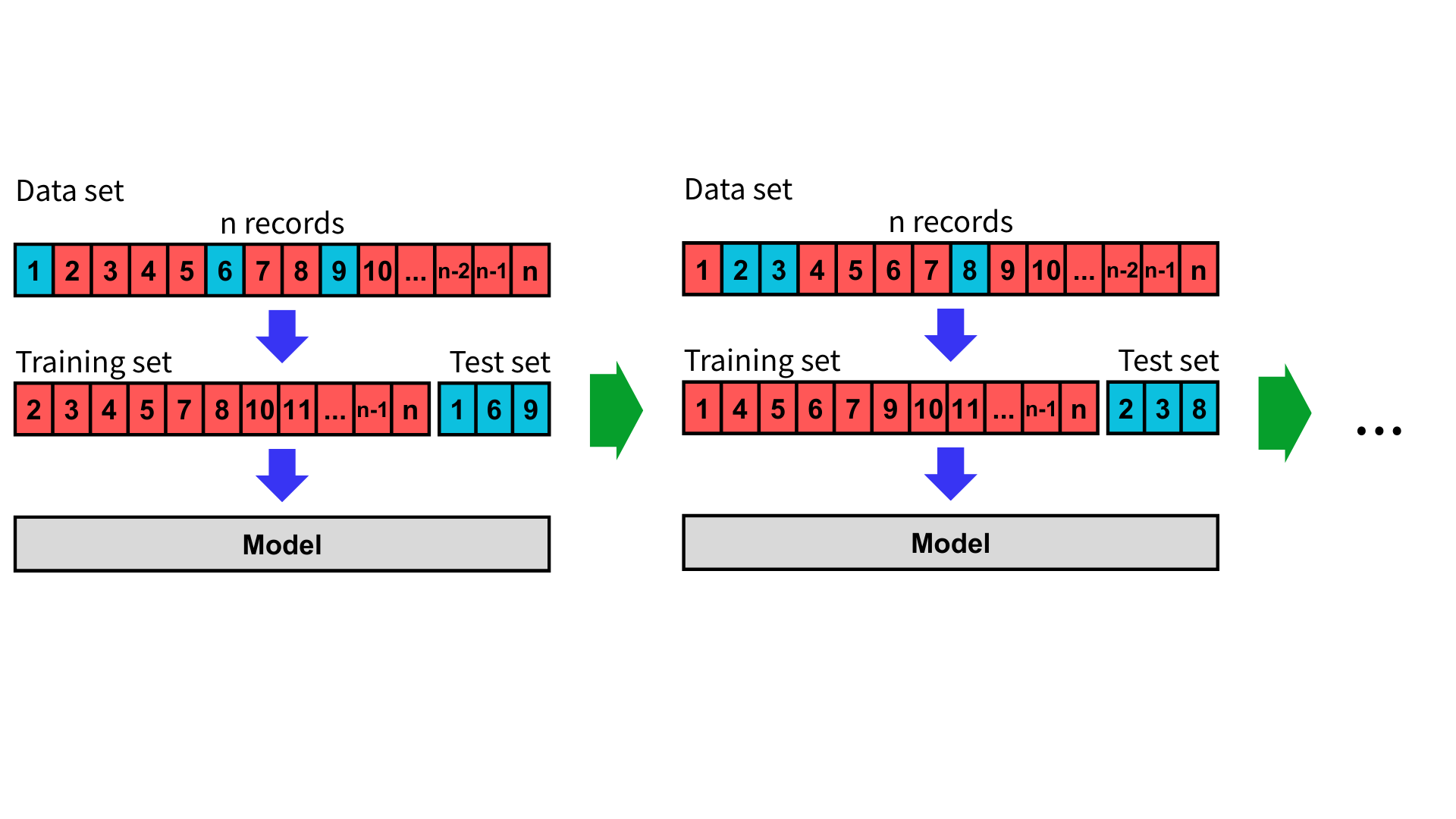
蒙地卡羅交叉驗證(Monte Carlo Cross-Validation, MCCV),也稱為隨機交叉驗證(Randomized Cross-Validation, RCV),是透過重複隨機切分資料集來評估模型泛化能力的方法。與 K 折交叉驗證不同的是,蒙地卡羅交叉驗證不保證每筆資料都會被用到,也不保證每次的訓練集或測試集大小完全一樣,且單筆資料可能多次做為測試集。
蒙地卡羅交叉驗證可視為將留出法執行多次,也因此資料拆分的方式可以很多樣化,但同時評估模型的偏差也很大。
作法
首先,指定訓練集與測試集的比例,以及重複次數。
接下來,重複執行隨機將資料集分成訓練集與測試集,進行訓練與評估模型。
執行完畢後,將評估指標取平均值與標準差並評估模型。
優點
- 可自由調整訓練集和測試集的比例與重複次數。
- 不需要劃分固定的 K 個子集或處理群組關係。
缺點
- 部分資料可能從未被用於測試,評估有偏差風險。
- 每次切分不同,結果可能變動較大,使結果依賴隨機性,需多次執行才能穩定。
- 不同次測試集中可能重複使用同一筆資料,不能保證測試集相互獨立。
適用情境
- 資料量充足,允許隨機抽樣多次。
- 希望快速估計模型效能,而不需複雜的分群問題。
- 大型資料集。
時間序列交叉驗證
時間序列資料具有明確的時間順序特性,未來的資料不應用於預測過去。若對時間序列資料使用 K 折交叉驗證等方法,可能會打亂時間順序,導致資料洩漏與不合理的評估結果。
時間序列交叉驗證(Time Series Cross-Validation, TSCV)是一種保留時間順序、只用過去預測未來的驗證方法,可避免未來資訊流入訓練資料。
作法
常見的方法有兩種,分別是擴增訓練法(expanding window)與滑動視窗法(sliding window)。
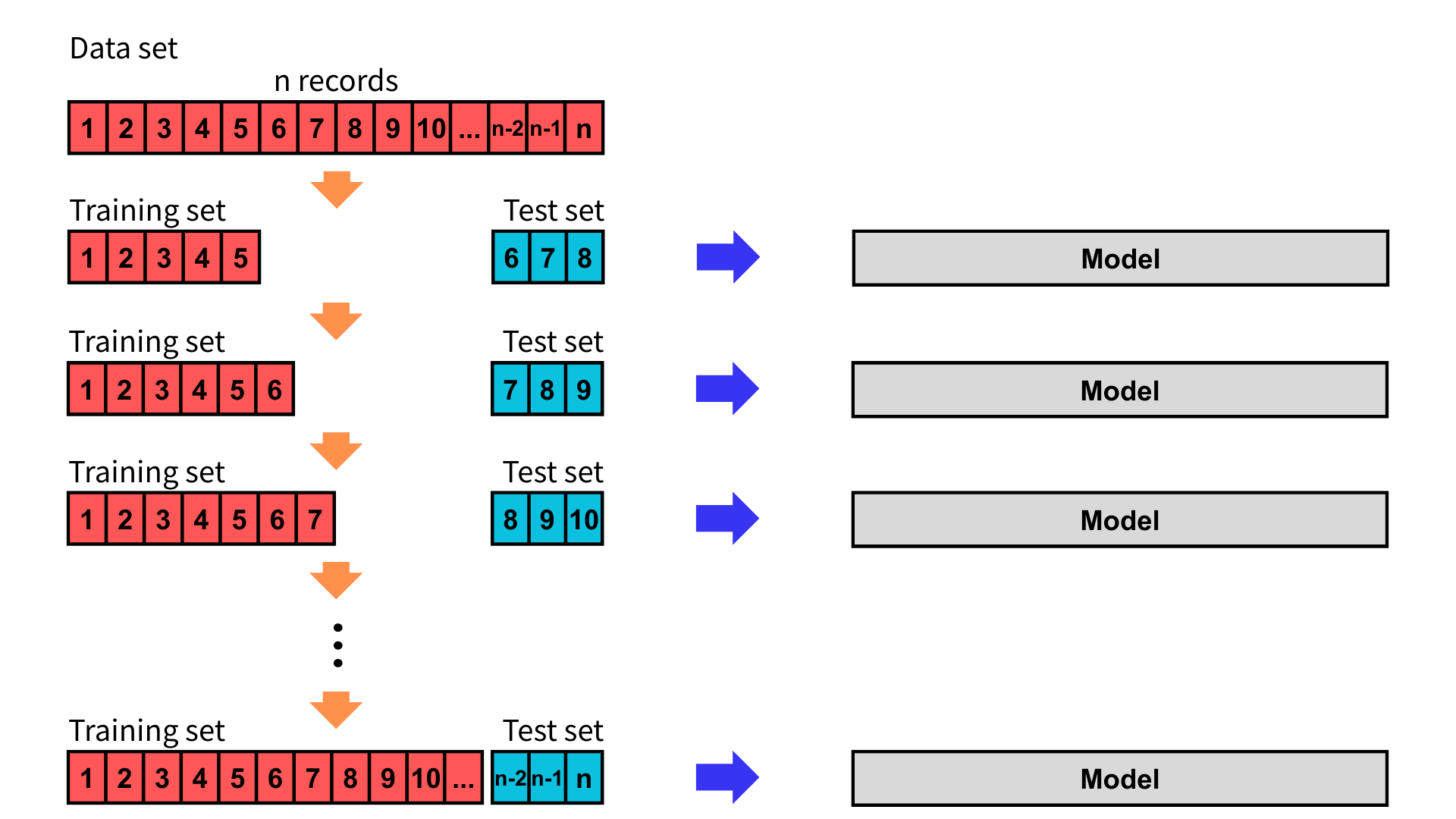
擴增訓練法
首先,將資料依時間排序,並設定初次的訓練集與測試集大小,測試集大小固定。其中,訓練集為某時間點過去的所有資料,測試集為該時間點未來的幾筆資料。
接下來,逐步增加訓練集的時間資料並訓練模型,而測試集也依時間往後移動,同時評估模型。重複此步驟直到用盡資料集。
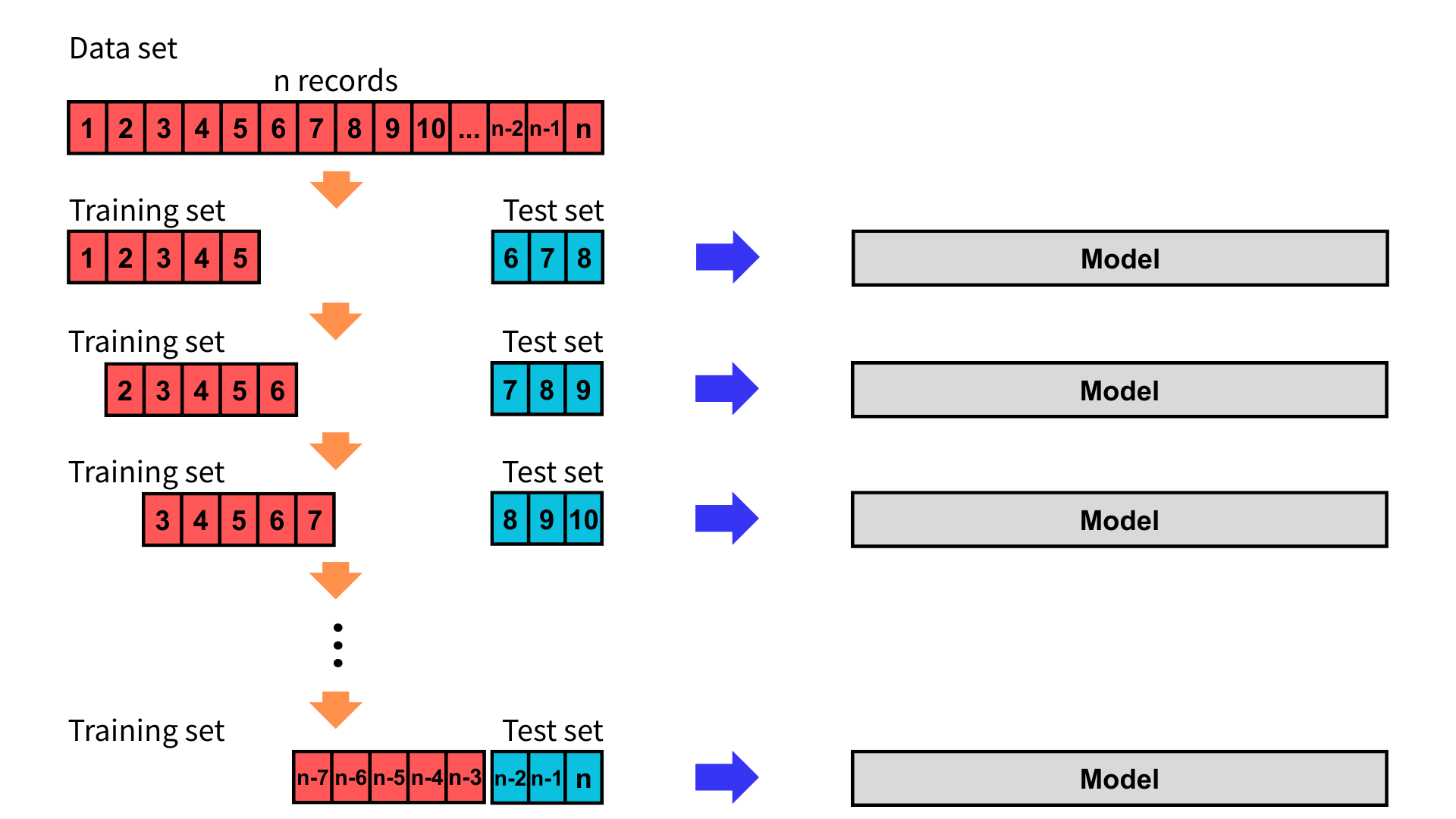
滑動視窗法
首先,將資料依時間排序,並設定每次的訓練集與測試集大小,訓練集與測試集大小固定。其中,訓練集為某時間點過去的所有資料,測試集為該時間點未來的幾筆資料。
接下來,逐步將訓練集與測試集依時間往後移動並訓練與評估模型,重複此步驟直到用盡資料集。
優點
- 保持時間順序,避免未來資訊外洩。
- 更貼近實際預測流程與真實部署情境。
- 可靈活調整訓練集和測試集比例與移動的視窗大小。
缺點
- 無法隨機打亂資料。
- 資料量較少時,測試樣本數可能不足。
- 當資料長度太長時,計算成本較高。
適用情境
- 時間序列資料分析,如股票、氣象、銷售等。
- 模型需嚴格遵循用過去資料訓練、預測未來的情況。
- 需要預測未來趨勢、事件或行為的情況。
方法比較
| 方法 | 計算成本 | 偏差 (Bias) | 變異數 (Variance) | 適用情境 | 優點 | 缺點 |
|---|---|---|---|---|---|---|
| 留出法 | 低 | 高 | 高 | 資料量大、快速評估 | 簡單、快速,適合大型資料集 | 單次評估不穩定,偏差大 |
| K 折交叉驗證 | 中 | 中 | 中 | 一般模型評估 | 子集數可調整,兼顧穩定與成本 | 計算成本較留出法高 |
| 分層 K 折交叉驗證 | 中 | 中 | 中 | 分類問題、類別不平衡資料 | 維持類別比例,評估更具代表性 | 與一般 K 折類似,僅適用於分類任務 |
| 留一交叉驗證 | 高 | 低 | 高 | 資料量極小 | 無偏估計,每筆資料皆被驗證 | 計算成本極高,容易過擬合 |
| 留 P 交叉驗證 | 極高 | 低 | 高 | 小型資料集,需完整泛化測試 | 理論上最完整的驗證方式 | 組合數過多,實作困難 |
| 重複 K 折交叉驗證 | 高 | 中 | 低 | 提升模型評估穩定性 | 降低隨機性影響,提高結果可靠性 | 計算成本高,超參數設計較多 |
| 分組 K 折交叉驗證 | 中 | 中 | 中 | 有群組資料 | 避免群組資料洩漏,更真實的泛化評估 | 需事先指定群組標籤,群組大小不均會影響表現 |
| 巢狀交叉驗證 | 極高 | 低 | 中 | 模型調參與評估並重視泛化能力 | 外層驗證避免過擬合,內層可調參 | 計算代價大,較複雜 |
| 蒙地卡羅交叉驗證 | 中~高 | 取決於切分策略 | 低~中 | 大型資料、快速穩定性評估 | 多次隨機切分避免偶然性,實作彈性高 | 可能出現重複樣本,無法保證覆蓋完整資料 |
| 時間序列交叉驗證 | 中 | 中 | 中 | 時間序列預測 | 保持時間因果性,避免資訊洩漏 | 無法隨機切分,視窗設計需考慮 |
結語
交叉驗證是評估模型泛化能力的核心方法。隨著不同大小的資料集與不同的資料特性,我們應該根據實際情況為模型選擇合適的交叉驗證方法,避免出現高估或低估模型表現。隨著模型愈來愈複雜、資料量日益增加,交叉驗證是現今機器學習的基礎,是幫助我們打造穩健、可泛化模型的重要工具。
參考資料
10程式中(2021年10月8日)。[Day 26] 交叉驗證 K-Fold Cross-Validation。iT邦幫忙。2025年5月1日參考自 https://ithelp.ithome.com.tw/articles/10279240
小千北同学超爱写代码(2021年1月19日)。StratifiedKFold和KFold的区别(几种常见的交叉验证)。博客园。2025年5月1日參考自 https://www.cnblogs.com/liuxiangyan/p/14299865.html
什么是:留P交叉验证。(無日期)。轻松学习统计。2025年5月1日參考自 https://zh-cn.statisticseasily.com/glossario/what-is-leave-p-out-cross-validation/
西红柿炒豆腐(2020年10月19日)。K-fold vs. Monte Carlo cross-validation(K折交叉验证与蒙特卡洛交叉验证(MCCV))。CSDN。2025年5月1日參考自 https://blog.csdn.net/weixin_44839513/article/details/109163111
交叉驗證。(2024年8月2日)。維基百科,自由的百科全書。2025年5月1日參考自 https://zh.wikipedia.org/zh-tw/交叉驗證
李航(2022年)。機器學習聖經:最完整的統計學習方法(初版)。深智數位股份有限公司。2025年5月1日參考。
新语数据故事汇(2023年12月9日)。一文带您了解交叉验证(Cross-Validation):数据科学家必须掌握的7种交叉验证技术。知乎。2025年5月1日參考自 https://zhuanlan.zhihu.com/p/671321268
数学人生(2015年11月7日)。留一法交叉验证和普通交叉验证有什么区别? 知乎。2025年5月1日參考自 https://www.zhihu.com/question/23561944
劉智皓(2021年2月7日)。機器學習_學習筆記系列(13):交叉驗證(Cross-Validation)和MSE、MAE、R2。Medium。2025年5月1日參考自 https://tomohiroliu22.medium.com/機器學習-學習筆記系列-13-交叉驗證-cross-validation-和mse-mae-r2-bc8fef393f7c
Claire Chang(2023年6月21日)。k-Fold Cross-Validation(交叉驗證)。Claire’s Blog。2025年5月1日參考自 https://claire-chang.com/2023/06/21/k-fold-cross-validation/
Cynthia(2025年2月20日)。訓練集、驗證集、測試集的定義與劃分。HackMD。2025年5月1日參考自 https://hackmd.io/@CynthiaChuang/What-is-the-Difference-between-Training-Validation-and-Test-Dataset
jingsongs(2017年9月8日)。KFold,StratifiedKFold k折交叉切分。CSDN。2025年5月1日參考自 https://blog.csdn.net/wqh_jingsong/article/details/77896449
ljalphabeta(無日期)。K折交叉验证评估模型性能。Gitbook。2025年5月1日參考自 https://ljalphabeta.gitbooks.io/python-/content/kfold.html
Hastie, T., Tibshirani, R., & Friedman, J.(2009)。The Elements of Statistical Learning: Data Mining, Inference, and Prediction(第2版)。Springer。2025年5月1日參考自 https://hastie.su.domains/ElemStatLearn/
James, G., Witten, D., Hastie, T., & Tibshirani, R.(2021)。An Introduction to Statistical Learning: With Applications in R(第2版)。Springer。2025年5月1日參考自 https://www.statlearning.com/
Kohavi, R.(1995)。A study of cross-validation and bootstrap for accuracy estimation and model selection。收錄於 Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI)(第2卷,第1137–1143頁)。2025年5月1日參考自 https://www.ijcai.org/Proceedings/95-2/Papers/016.pdf