發佈日期 / 更新日期
隨筆 #5
圖片壓縮工具
在平時建立網站頁面時,我們會發現有時候有些頁面需要讀取一段時間才能出現,而有些頁面卻沒有。經過比較不同網頁後得出一個結論,網頁內的圖片如果大小過大,會造成網頁讀取速度較慢,因此萌生出要找到一款能夠壓縮目前網站目錄下所有圖片工具。但找來找去,網路上都沒有找到合適的應用程式,最後決定自己製作一款能夠壓縮所有圖片的程式。
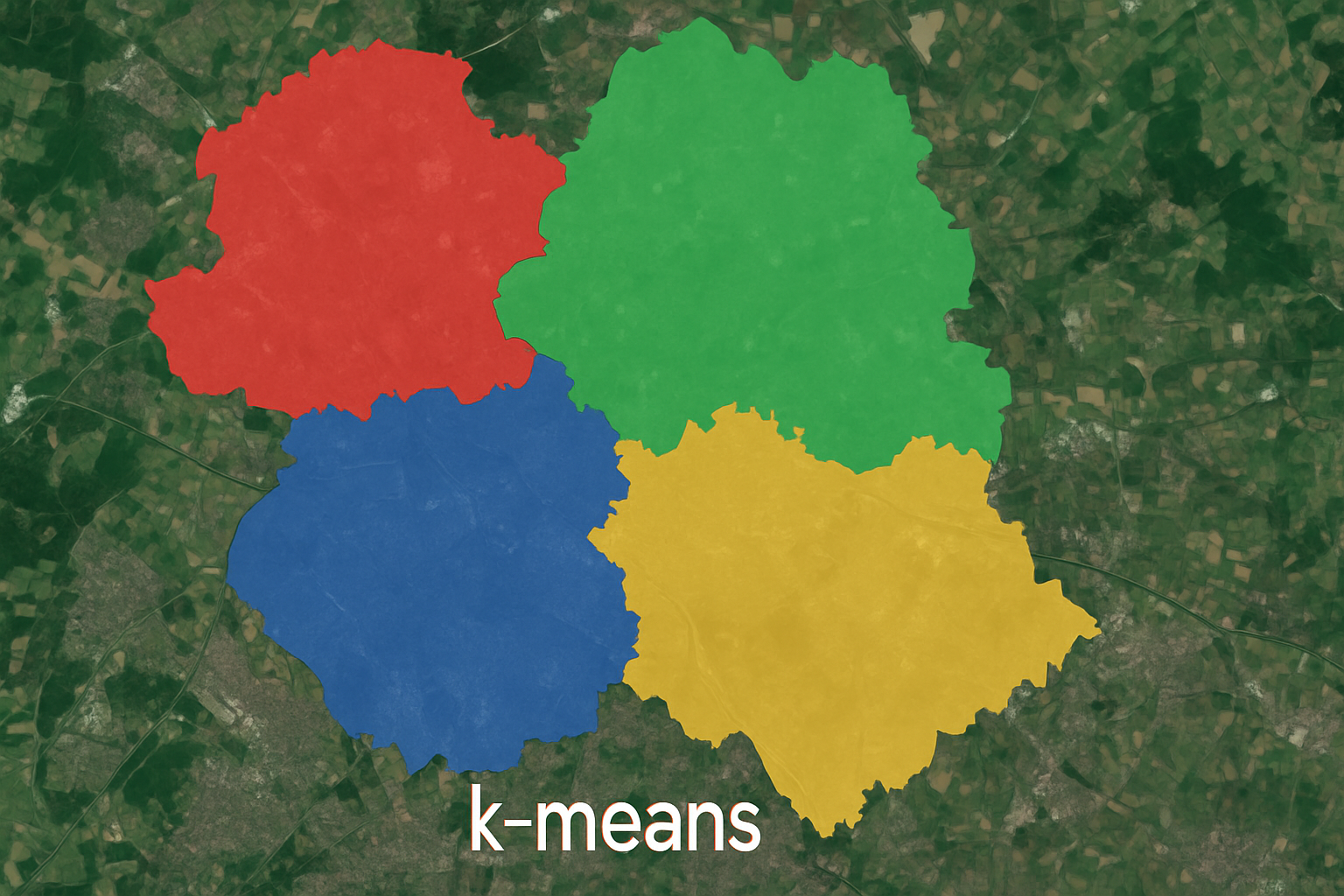
k-平均聚類分析
k-平均聚類分析(k-means clustering),在中文地區常被稱為 k-平均演算法,簡稱 k-means。這是一種將 $n$ 個資料點分成 $k$ 個群集(clusters)的分群方法,使得每一個點都能歸屬於距離它最近的群集中心(centroid)。
標準化的方法
在進行統計分析時,往往會接觸到各種類型的資料,而這些資料可能具有不同的單位與數值範圍。為了消除單位差異所帶來的影響,並提升資料之間的可比性,常需透過適當的尺度轉換來進行標準化處理,也就是讓它們在同一個尺度下進行分析。根據應用需求的不同,標準化的方法也各式各樣,不同方法所帶來的差異,甚至可能左右後續的統計推論與模型表現。
A* 演算法
A* 演算法(A* Algorithm),又稱作 A* 搜尋演算法(A* Search Algorithm),是眾多遊戲與人工智慧應用中常見的路徑規劃演算法之一。其演算法結合戴克斯特拉演算法的全局最短路徑特性與貪婪演算法的啟發式搜尋策略,使 A* 演算法兼具效率與準確性,因此廣受歡迎。同時, A* 演算法也廣泛用於機器人導航、地圖路徑規劃等等眾多領域中。
淺談貪婪演算法
貪婪演算法(Greedy Algorithm)是一種透過每一步都選擇目前看起來最有利的選項進行求解的演算法,透過簡單且直觀地判斷在當前所有選擇中的最優解,並期望這些局部的選擇能累積成整體的最佳解,直到滿足終止條件為止。由於貪婪演算法僅專注於當下的局部環境,故選擇的解法不一定是全局的最優解,甚至可能會繞遠路。但不可否認的是,由於貪婪演算法不考慮全局,僅對局部選項做決策,因此通常具有相當高的執行效率。
戴克斯特拉演算法
戴克斯特拉演算法(Dijkstra's Algorithm)是探討最短路徑的一種演算法,最早是用於尋找兩點間的最短路徑,後拓展到由固定一點尋找與其他點的最短路徑,稱為該點的「最短路徑樹」。
在 LoveIt 主題的文章中新增相關文章區塊
常用的距離度量方法
封面圖片由 ChatGPT 生成。
前言
如何計算距離是現今統計分析中重要的一個環節,選擇不同的距離度量方式對於統計分析方法可能會產生不同的結果。以下介紹常用的距離度量方法。