臺鐵志學站停車場停車模擬模型建立專題

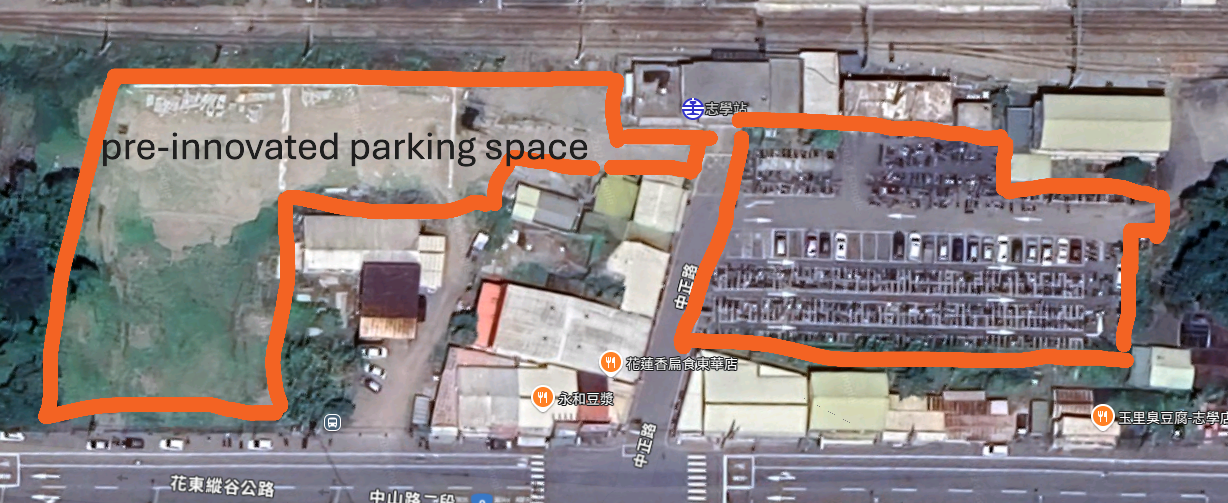
封面圖片為臺灣鐵路股份有限公司志學車站及周邊停車設施， 2024 年 12 月 29 日擷取自 Google 地圖。

緒論

志學車站是位於花蓮縣的鐵路車站之一，鄰近國立東華大學（National Dong Hwa University, NDHU），服務當地居民與東華大學的學生。該車站常常面臨停車位不足的問題，在假日與週末期間尤為嚴重，但由於缺乏維護與管理意識，車位不足的問題對附近大學的學生造成了相當大的影響，並給志學村的當地居民帶來諸多不便。

當我們得知志學車站的停車場將進行改建（國立東華大學, 2023）時，我們開始好奇，在改建後的停車位短缺情況會改善多少。

為了探討這個問題，我們對車站出入口的人流進行了調查，並收集了居民、學生與上班族的通勤模式、交通方式及其他相關資料。我們的目標是透過模擬實驗，比較停車場改建前後的情況。由於時間限制，本報告將專注於平日（週一至週四）停車場車流的模擬。

研究動機與背景

身為東華大學的學生，我們經常在繁忙時段面臨停車位不足的情形，而類似的情況在許多鄰近學校與社區住宅的大眾運輸站點也很常見。這個問題不僅困擾著我們，也促使我們思考如何找到更有效的解決方式。隨著各種車輛的數量不斷增加，而可利用的土地卻相對有限，停車需求與供給之間的落差便愈加明顯。

在志學車站，停車位不足同時影響依賴車站通勤的東華學生與當地居民。雖然車站停車場已規劃進行改建，但若沒有適當的研究作為支撐，我們無法確定改建是否能真正改善問題，或是否只是將壓力轉移至其他區域。因此，本研究希望透過資料蒐集與分析，更清楚地呈現當前的停車狀況，並預測改建後可能出現的變化。

研究目標與範疇

本研究的主要目標是評估志學車站停車場改建計畫對緩解停車位不足問題的影響。為達成此目標，我們將著重於以下部分：

• 根據蒐集的資料，建立平日（週一至週四）的完整車流模型。
• 模擬改建前與改建後的停車情境，以評估改建方案的有效性。
• 探討造成停車位短缺的關鍵因素，例如尖峰時段、通勤模式與使用者特性。
• 提出具體可行的建議，作為協助改善後續停車設施與交通管理的方向。

研究方法

首先，我們依據預期的模擬需求，使用 Google 表單設計問卷，以蒐集進行模型建置所需的相關資料。此問卷的目的在於取得足以支持建立後續模擬模型的有效資訊。

接著，參考王家禮老師課程內容（王家禮, 2024）及 A. M. Law 與 W. D. Kelton 所著《Simulation Modeling and Analysis》（2007，第四版），我們將模擬實驗拆解為核心構成要素：變數、事件、計數器及流程圖。透過此系統化的拆解方式，我們能更直觀地理解模擬程序中的每個步驟。

最後，我們建立了一套完整的模擬實驗架構，並可透過調整初始參數來執行不同情境下的模擬，以供比較與分析。

問卷與資料蒐集

為取得所需資料，我們在志學車站進行了問卷調查。問卷內容共包含五項問題：交通目的、旅客是進站或出站、停放於車站的交通工具種類、偏好的交通方式，以及是否願意支付停車費。我們以 QR Code 連結至 Google 表單，並於現場詢問旅客以協助填答。

資料蒐集的時段集中於兩個尖峰時段：早上 6:00 至 8:00，以及傍晚 5:00 至 7:00。選擇這兩段時間的原因是在地居民與學生多半會於早上搭乘火車通勤上班或上課，並於傍晚返回。

問卷調查的進行時間為週三至週四，不包含週一、週五與週末。之所以排除這些日子，是因為其旅客活動較不規律，無法代表典型的尖峰時段特性。

狀態變數

• 時間變數

  在本次模擬中，我們使用兩個時間變數：t 與 clock。其中，t 代表模擬當前的時間，而 clock 則表示一天中的實際時間（24 小時制）。

• 旅客人數

  用於記錄旅客數量，以及汽車、機車、自行車與行人的進出站情況，並儲存在 passenger_list 中。

• 停車位

  我們分別使用 remain_car_parking_space 與 remain_motorcycle_parking_space 來記錄剩餘的汽車與機車停車位數量。由於志學車站並無專用自行車停車區，自行車會使用機車停車位。考量車格大小，我們設定一個機車車格可容納兩輛自行車。

• 已停放車輛

  用於記錄停車場內車輛的停放狀態，例如 car_parked、motorcycle_parked 以及 bicycle_parked。

事件類型

• 更新事件

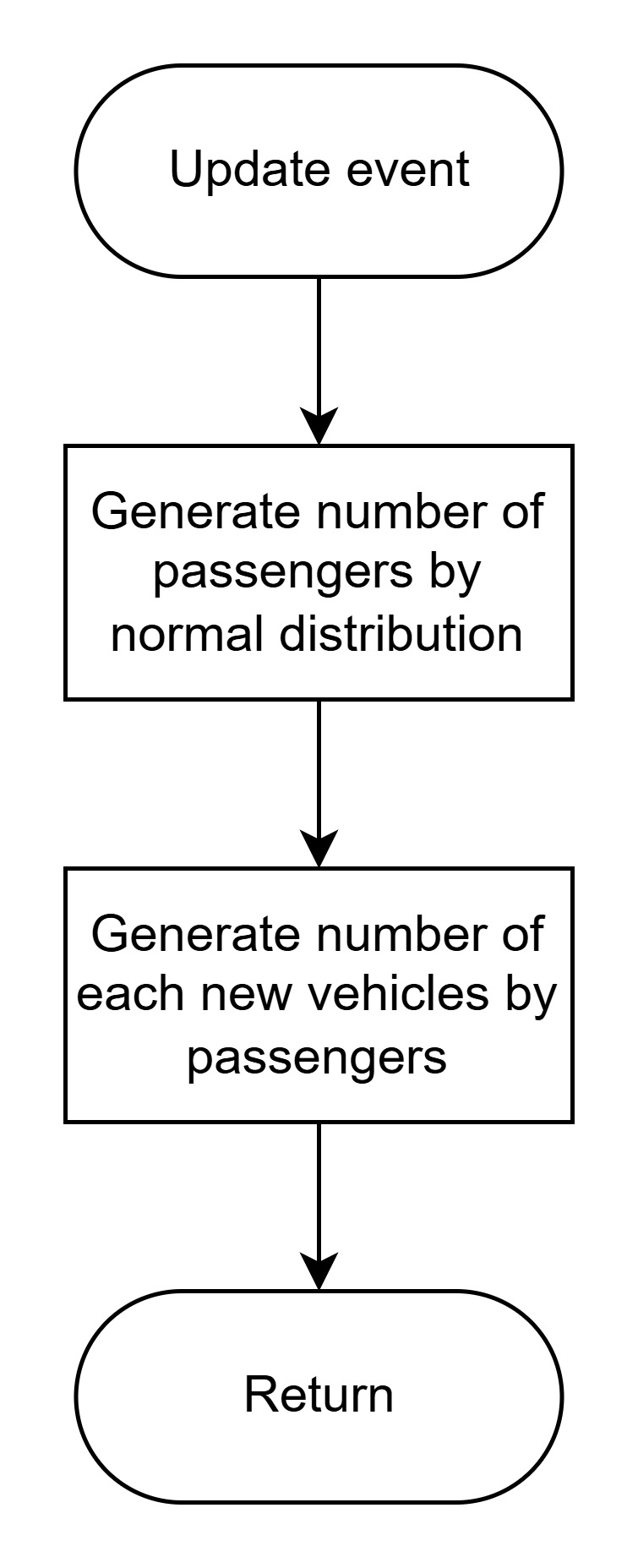
  更新事件用於根據常態分布生成每小時的旅客人數。利用生成的旅客數量，我們進一步計算停車場中各類車輛的進出數量。

• 自行車與車輛停放事件

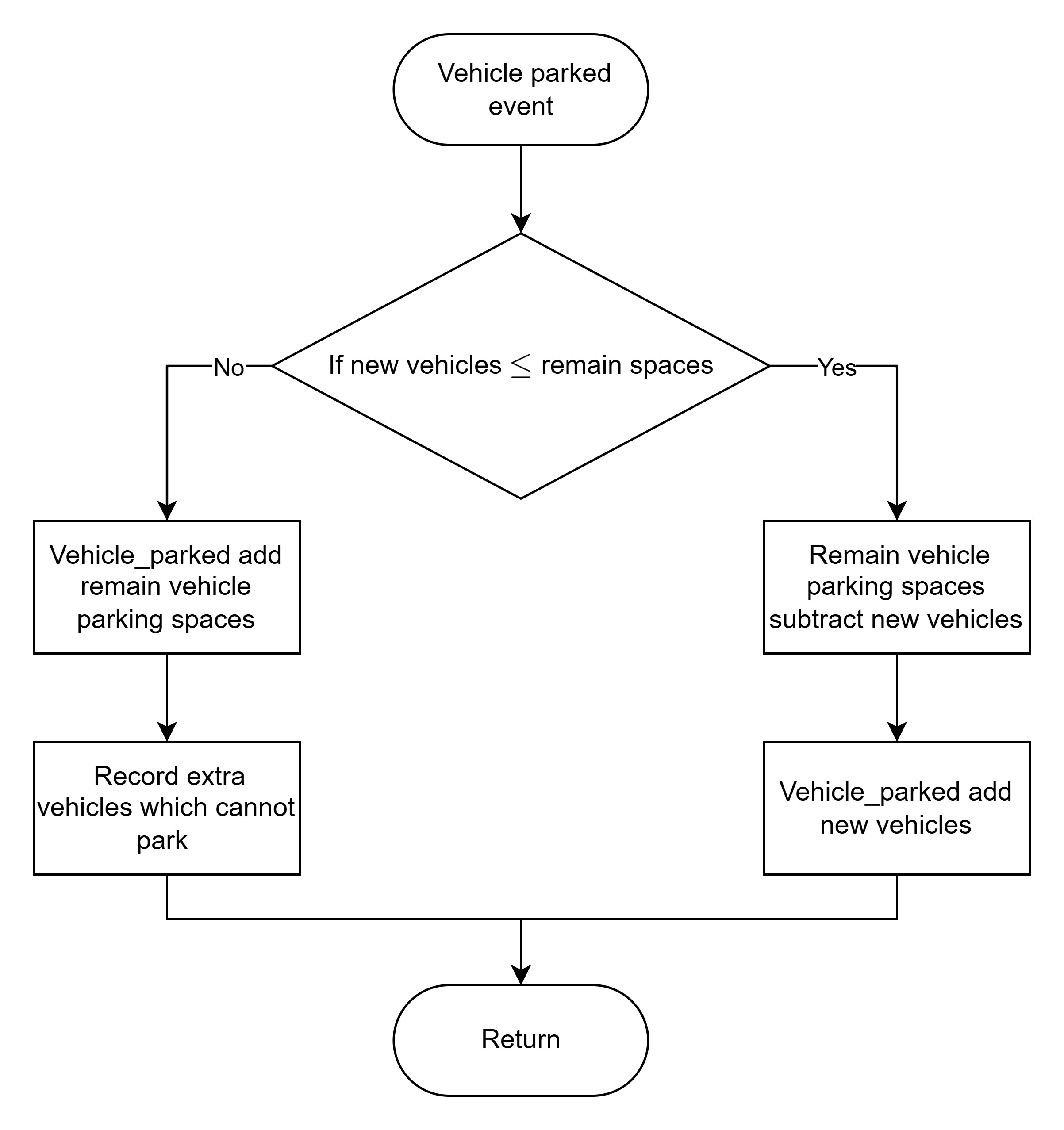
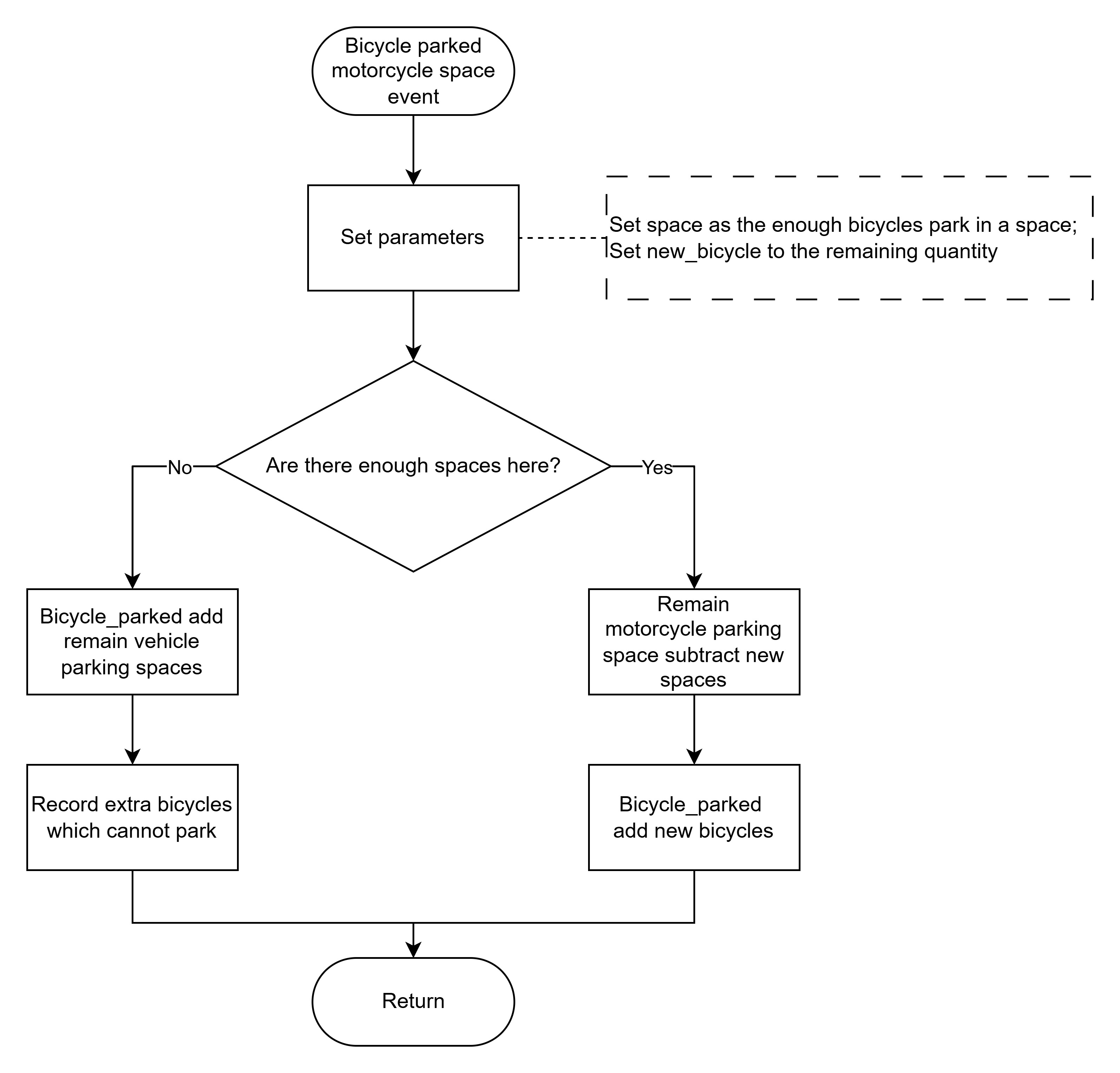
  為更貼近實際情況，除了建立 vehicle_parked_event 外，我們也專門設計了 bicycle_parked_in_motorcycle_space_event 來處理自行車的停放。為簡化模擬工作量，我們假設自行車會優先停放在已經有其他自行車的機車車格中。

• 自行車與車輛離場事件

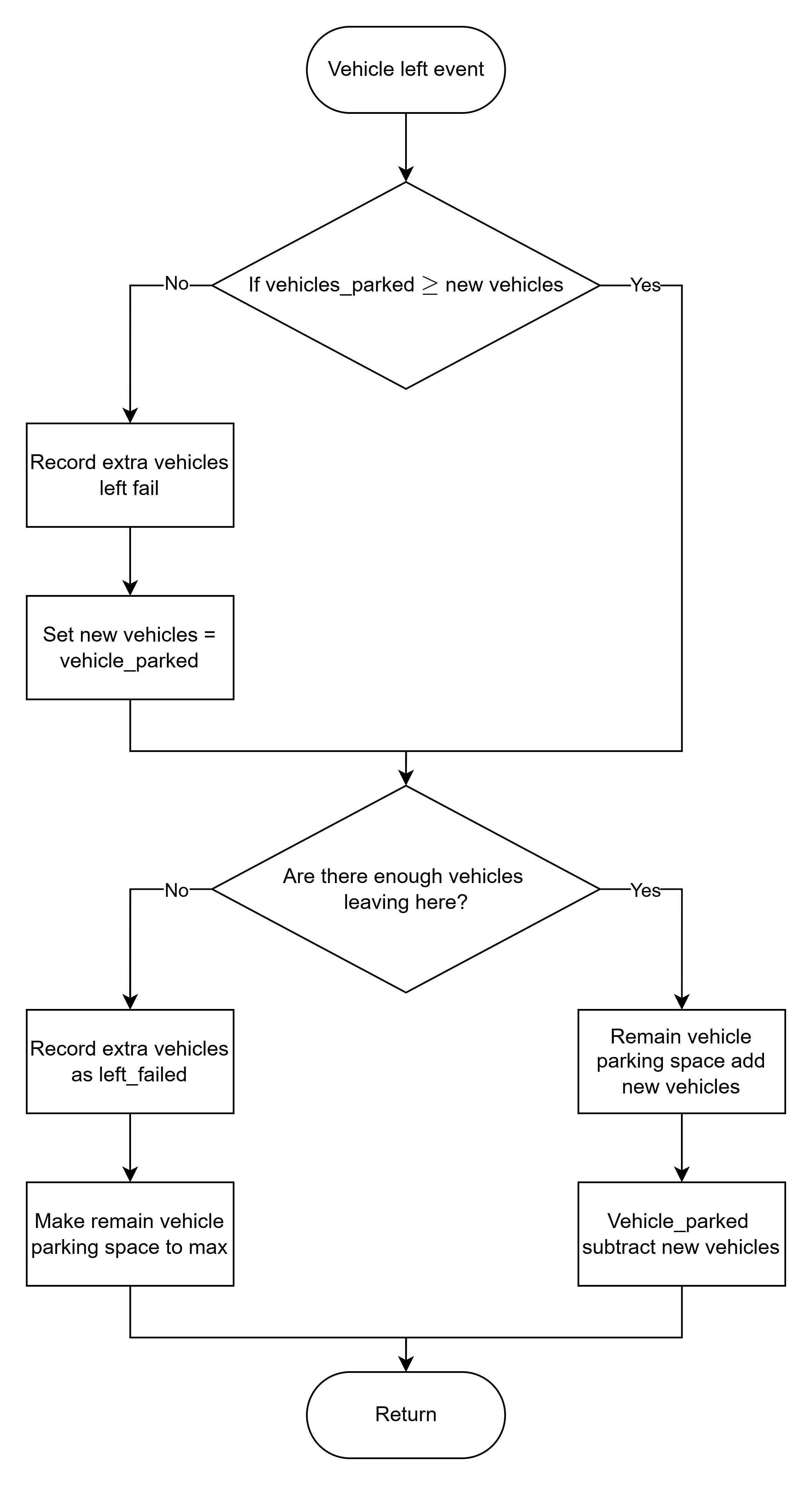
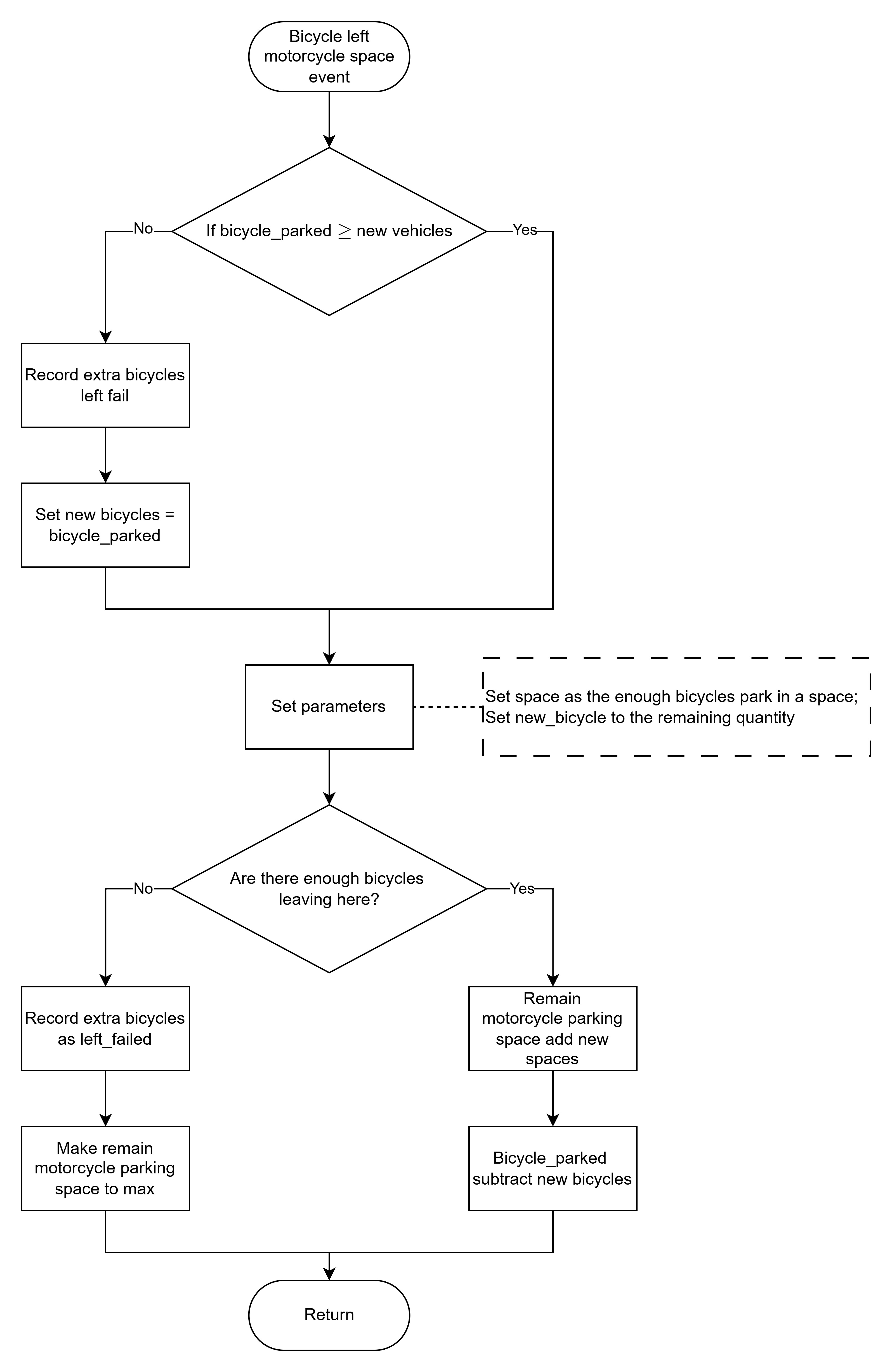
  類似於前述事件，除了建立 vehicle_left_event 外，我們還建立了 bicycle_left_motorcycle_space_event，以模擬自行車的離場情況。

流程圖

為了更有效地進行模擬，我們製作了以下流程圖。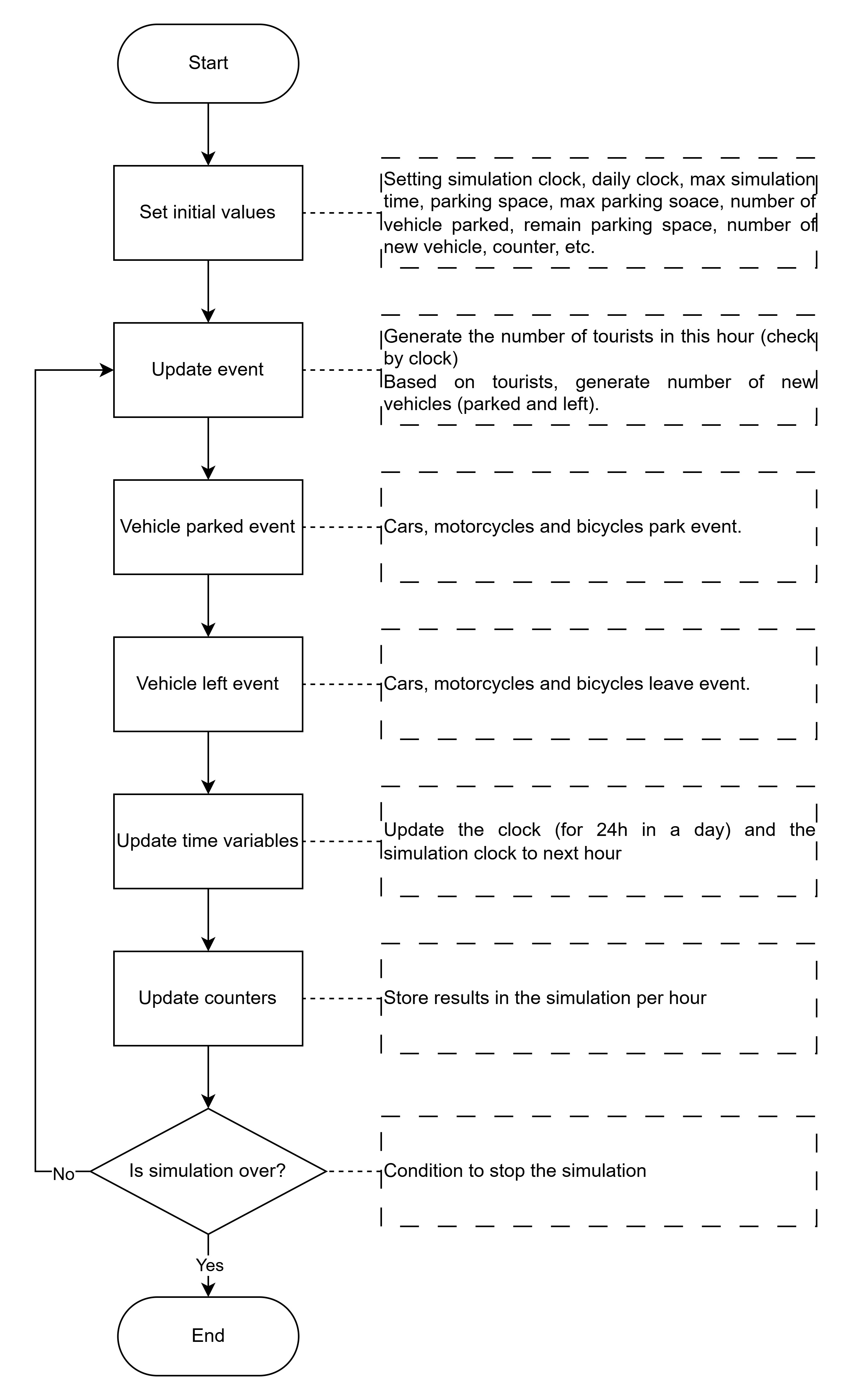

變異數縮減：控制變數法

對於 $i = 1, 2, \cdots, 24$，車站在第 $i$ 小時的旅客人數 $P_i$ 服從平均值為 $\mu_i$、變異數為 $\sigma_i^2$ 的分布。並且對於 $i = 1, 2, \cdots, 24$，給定以下常數參數：

• $\mu_i$ 與 $\sigma_i^2$。
• 第 $i$ 小時進入車站的旅客比例 $a_i$。
• 第 $i$ 小時進出車站旅客使用自行車、汽車與機車的比例，分別為 $b_{in_i}$、$b_{out_i}$、$c_{in_i}$、$c_{out_i}$、$m_{in_i}$、$m_{out_i}$。

我們定義第 $i$ 小時停車場內的自行車、汽車與機車數量如下： \begin{align*} & B_i = B_{i-1} + P_i \times a_i \times b_{in_i} - P_i \times (1 - a_i) \times b_{out_i} \\ & C_i = C_{i-1} + P_i \times a_i \times c_{in_i} - P_i \times (1 - a_i) \times c_{out_i} \\ & M_i = M_{i-1} + P_i \times a_i \times m_{in_i} - P_i \times (1 - a_i) \times m_{out_i} \\ \end{align*}

需注意第 $1$ 小時停車場內的自行車數量為： \begin{align*} B_1 = B_{24}(\text{last day}) + P_1 \times a_1 \times b_{in_1} - P_1 \times (1 - a_1) \times b_{out_1}. \end{align*}

若我們模擬 $N$ 天，則對於 $i = 1, 2, \cdots, 24$，第 $i$ 小時停車場內自行車、汽車與機車數量的樣本平均值為： \begin{align*} & \overline{B_i} = \frac{1}{N} \sum_{n = 1}^{N} B_{i_n}, \\ \end{align*} 汽車與機車的平均值類似，分別為 $\overline{C_i}$ 與 $\overline{M_i}$。

我們對 $\overline{B_i}$、$\overline{C_i}$ 與 $\overline{M_i}$ 分別採用控制變數法。則第 $i$ 小時停車場內自行車、汽車與機車數量的估計值如下： \begin{align*} & \overline{B_i} + \overline{c_{i_1}^*}(\overline{P_i} - \mu_i) \\ & \overline{C_i} + \overline{c_{i_2}^*}(\overline{P_i} - \mu_i) \\ & \overline{M_i} + \overline{c_{i_3}^*}(\overline{P_i} - \mu_i) \end{align*} 其中， \begin{align*} \overline{c_{i_1}^{*}} = -\frac{\overline{Cov}(B_i, P_i)}{Var(P_i)} = -\frac{\overline{Cov}(B_i, P_i)}{\sigma_i^2} \end{align*} 且 \begin{align*} \overline{Cov}(B_i, P_i) = \frac{1}{N} \sum_{n = 1}^{N} (B_{i_n} - \overline{B_i})(P_{i_n} - \mu_i) \end{align*} 汽車與機車的控制變數係數分別為 $\overline{c_{i_2}^*}$ 與 $\overline{c_{i_3}^*}$，計算方法類似。

模擬與實驗結果

實驗環境

• 硬體環境

  • 處理器 (CPU)：Intel Core(TM) i7-13700
  • 記憶體 (RAM)：32GB DDR4
  • 顯示卡 (GPU)：無
  • 作業系統：Windows 11 專業版（版本 24H2，作業系統編號 26100.2605）

• 軟體環境

  • 程式語言：Python 3.12.8
  • 開發工具：Visual Studio Code (v1.96.2)
  • 相關函式庫：
    • numpy (v2.2.1)
    • pandas (v2.2.3)
    • tqdm (v4.67.1)
    • matplotlib (v3.10.0)
    • imageio (v2.36.1)

三種模擬情境

我們進行了三種模擬情境：不限停車位、現有停車位與擴增後停車位。

• 不限停車位

  在此情境下，我們假設停車容量不受限制，由系統自行決定進出車站的人數。目標是計算在一般時段及尖峰時段，停放於車站的自行車、機車與汽車數量。

• 改建前停車場

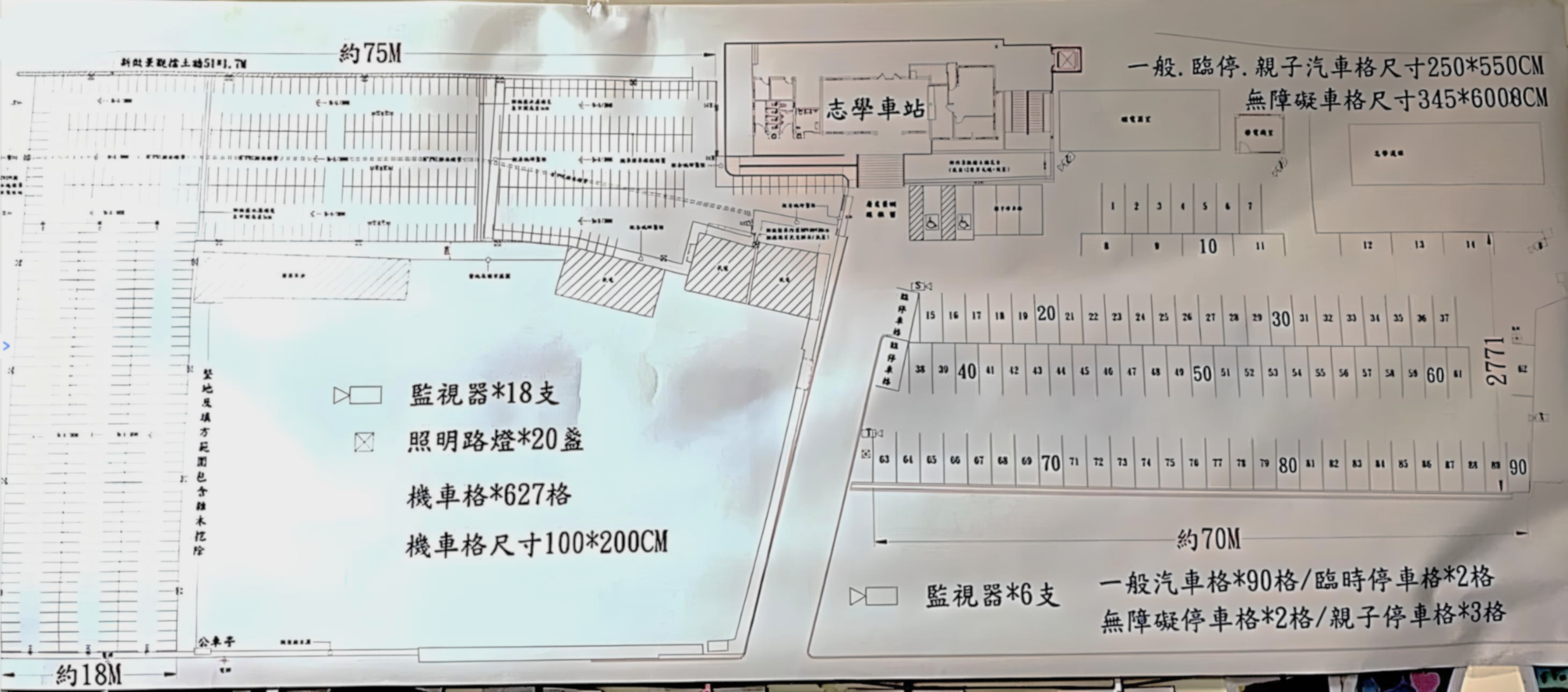
  根據對志學車站的調查，我們計算了現有指定停車位的數量。此情境旨在了解現有停車設施的容量，以及其滿足需求的能力。

• 改建後停車場

  此情境探討增加停車容量可能帶來的效益。改建的目的在於減輕停車位不足所造成的壓力，並提升整體可達性。

情境 1：不限停車位

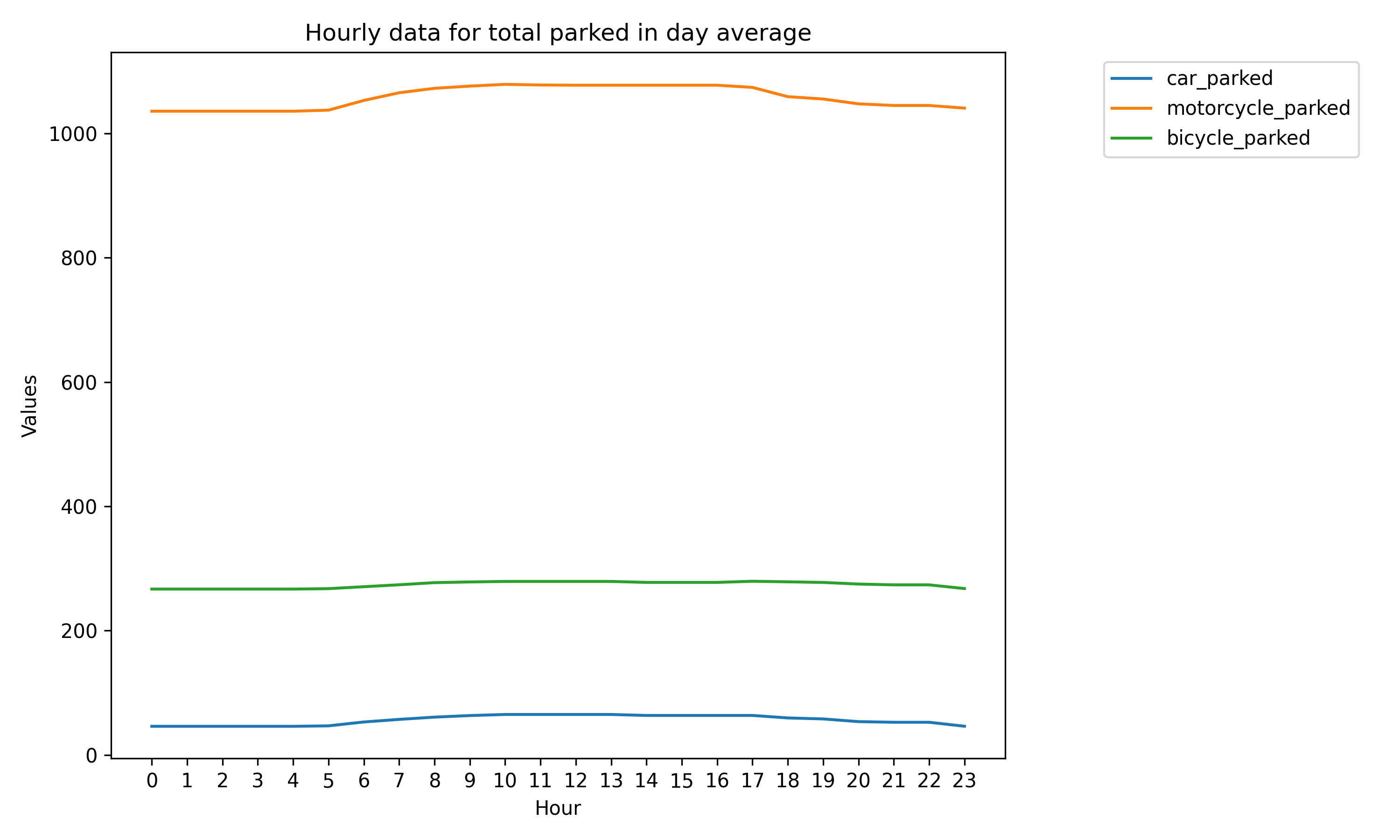
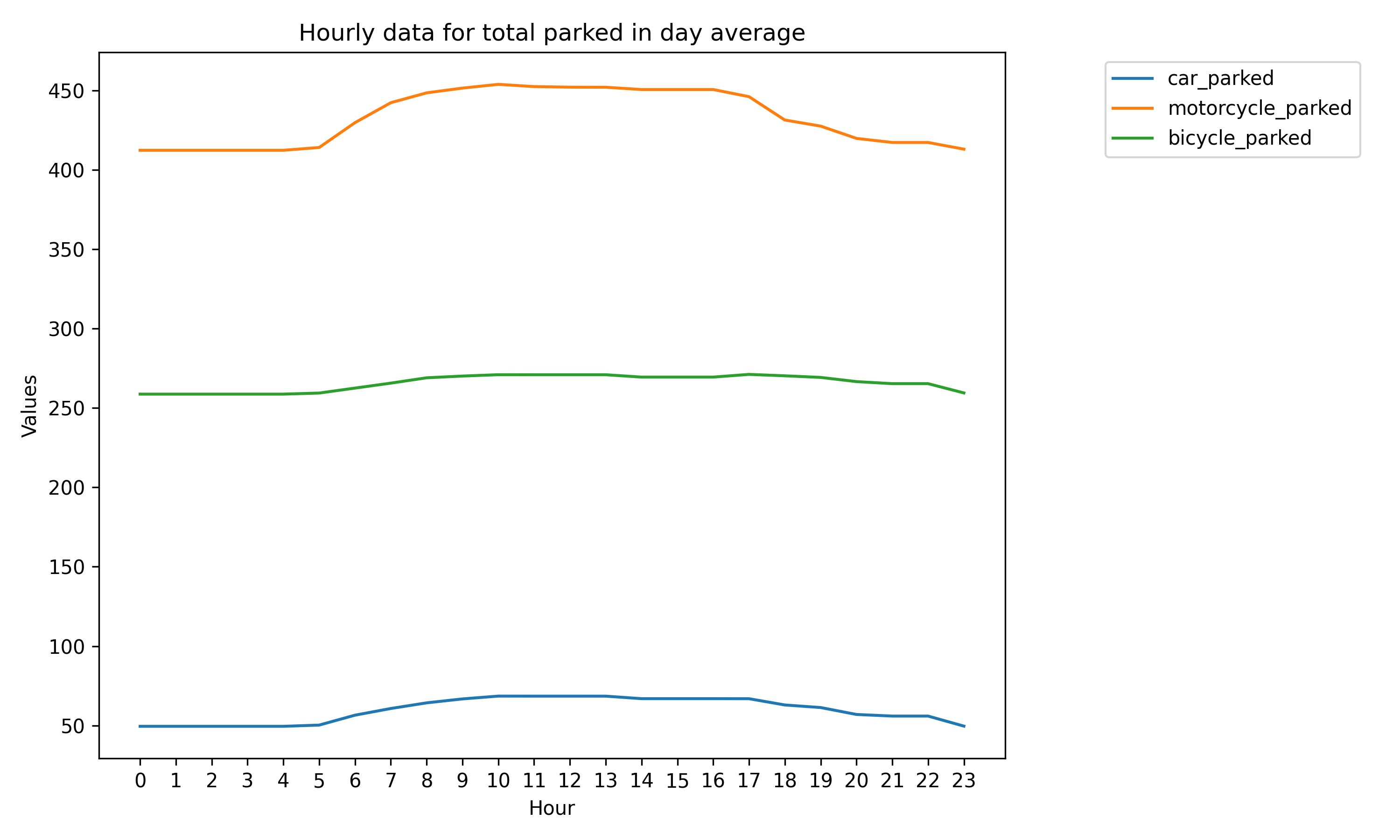
在不限停車位的情境下，我們的模擬結果顯示，當維持進出站旅客比例為 1:1.6 時，停放的汽車、機車與自行車數量會隨時間逐漸增加。這表示在一般平日條件下，我們的模型顯示每日需求略高於前一天的需求。

情境 2：改建前停車場

在此情境下，我們設定停車位數量，模擬停車場改建前平日時段車輛數量的變化。

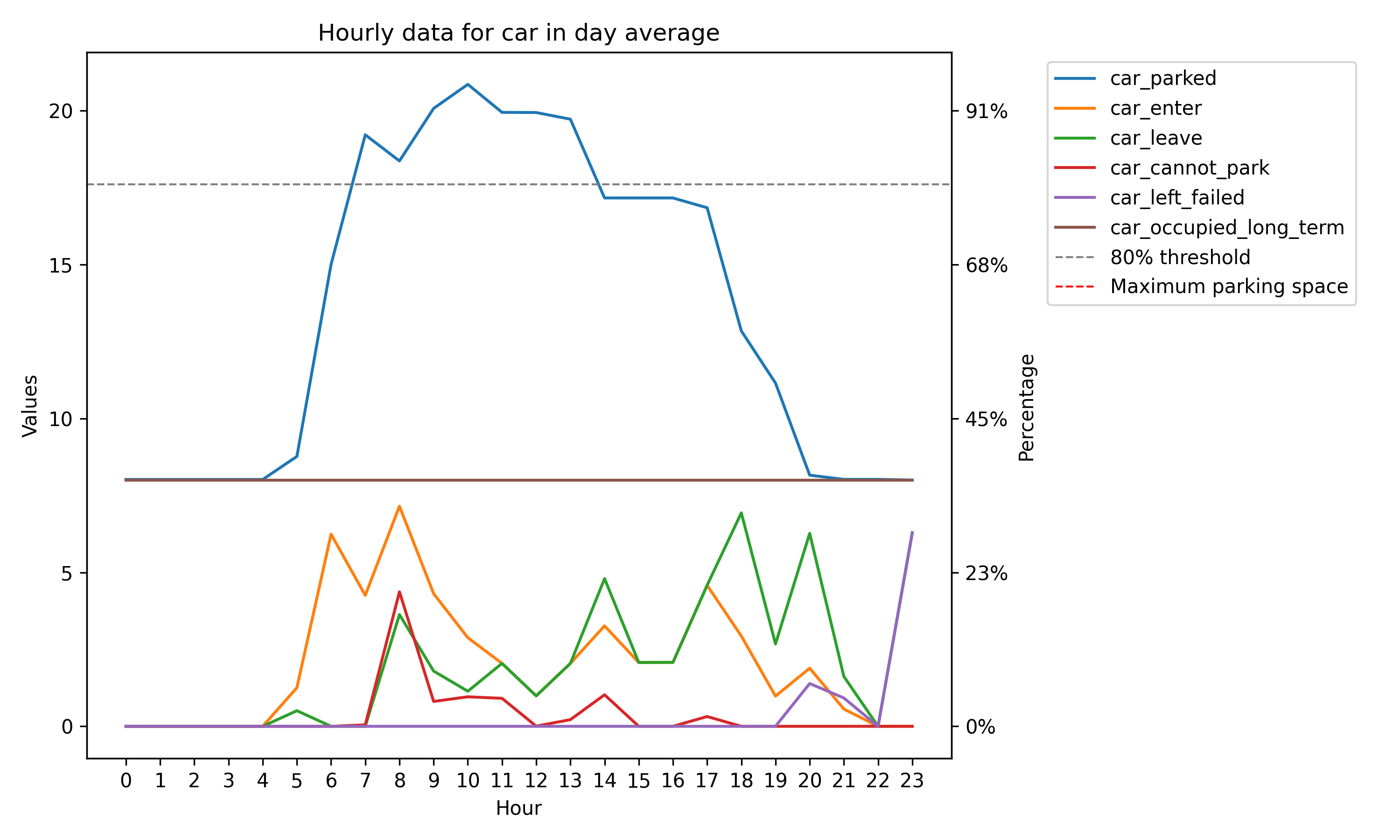
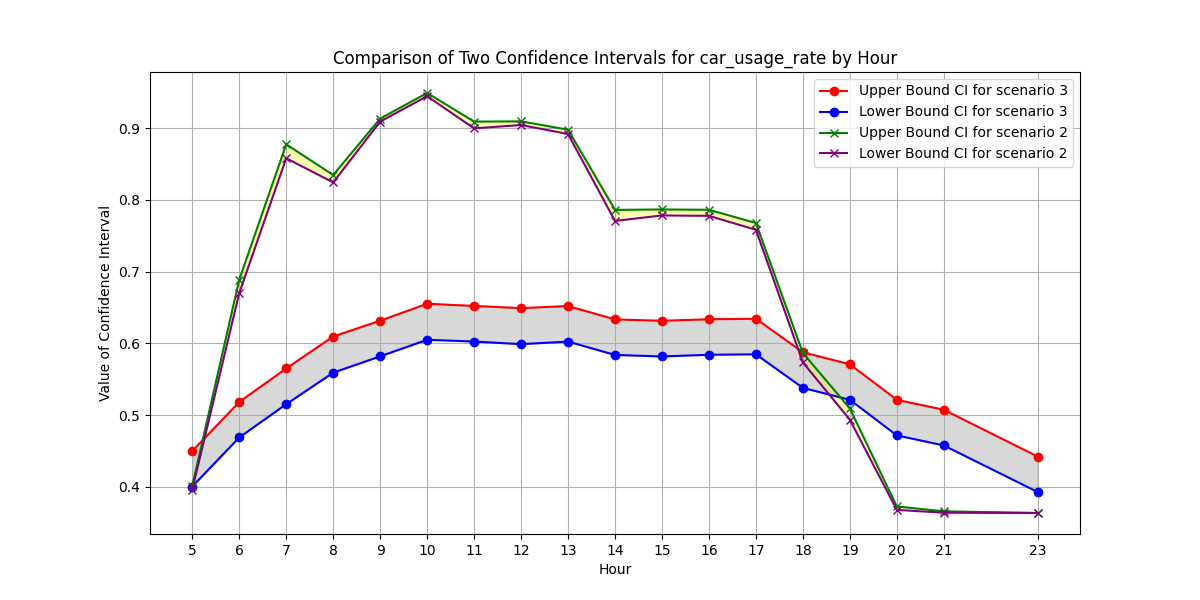
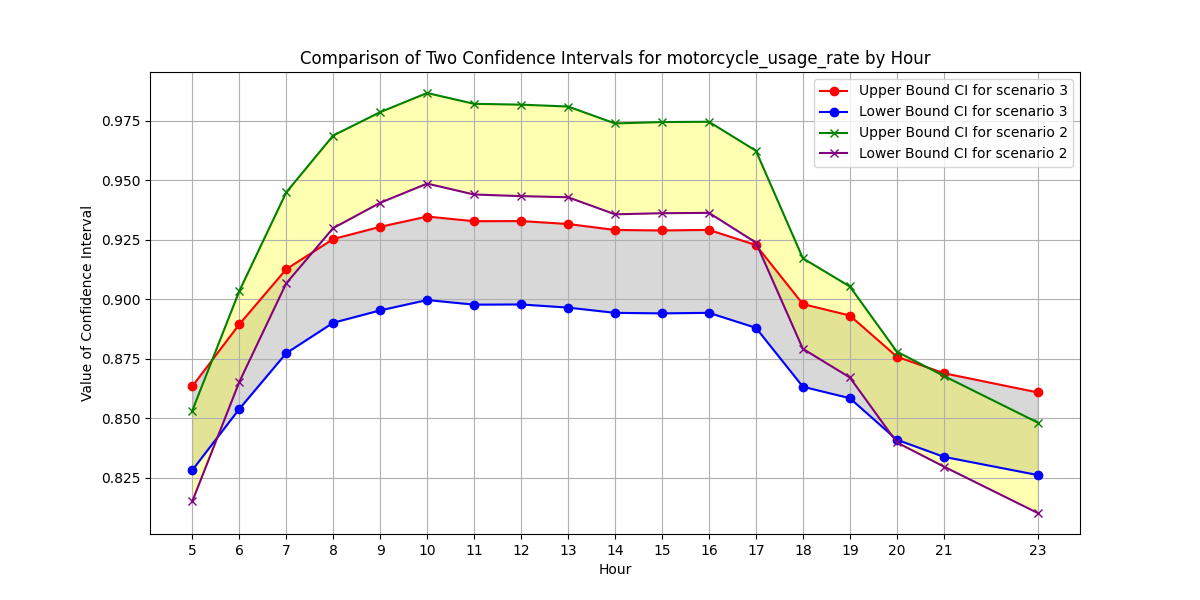
在此情境中，我們觀察到兩個主要趨勢：首先，對每日數據而言，汽車、機車與自行車數量從 7:00 到 17:00 呈下降趨勢，最後趨於穩定。此外，汽車進出數量動態波動，呈現一定的分布特性。其次，改建前的停車場可容納約 600 輛以上的機車與自行車，以及約 50 輛汽車。

情境 3：改建後停車場

在此情境下，我們設定停車位數量，模擬停車場改建後平日時段車輛數量的變化。

改建後的停車場增加了停車容量，可容納更多車輛。因此，停車場現可容納約 1000 至 1200 輛機車與自行車，以及約 60 至 70 輛汽車。

結論與討論

在本專案中，我們對志學車站進行調查，以獲取車輛與旅客進出車站的流量。為了全面了解車站停車狀況，我們使用 Google 表單進行問卷調查，問題內容包括旅客進出車站的情況、到站的交通工具類型，以及是否願意支付停車費。在模擬研究中，我們設定了三種情境：不限停車位、改建前停車場以及改建後停車場。我們主要關注停放於車站的車輛數量，其它變數則用於檢查程式碼的正確性。

研究結果顯示，改建後停車場的容量增加，能更有效地滿足停車需求。此外，長時間停放是造成停車位不足的主要原因。

未來工作

未來，我們將持續優化此模型，納入週末、假日及其他相關因素的資料，以進一步精進模擬結果。

由於時間與資料的限制，本研究目前僅針對平日情境進行模擬。未來的擴展方向包括：

• 蒐集週末與假日資料，以涵蓋更廣泛的通勤行為。
• 整合更多因素，如天氣狀況與特殊事件的影響。
• 與地方政府合作，優化模型並落實實際解決方案。
• 探討停車費對停車需求的影響。

參見

• 我們的 GitHub 專案：https://github.com/Josh-test-lab/parking-lot-simulation。

• 原始報告下載。

參考資料

• 李婉寧. (2015). 路外停車場服務評鑑指標設計之研究：以台北市公有委外平面停車場為例. 臺灣博碩論文知識加值系統. https://hdl.handle.net/11296/zzqjxr
• 法務部. (2022). 利用空地申請設置臨時路外停車場辦法. 全國法規資料庫. https://law.moj.gov.tw/LawClass/LawAll.aspx?pcode=K0040034
• 張存薇. (2018). 台東火車站汽機車停車收費 10月上路. 自由時報. https://news.ltn.com.tw/news/life/breakingnews/2555469
• 國立東華大學. (2023). 花蓮縣議會徐雪玉副議長協調臺鐵局增設志學站前停車場，解決東華學子及居民停車問題. 東華新聞. https://www.ndhu.edu.tw/p/406-1000-213698,r4956.php?Lang=zh-tw
• 國營臺灣鐵路股份有限公司. (2023). 停車場收費標準一覽表. https://www.railway.gov.tw/tra-tip-web/tip/file/bc00c5d2-2184-4dbd-bbc4-530a9a3fb83a
• 國營臺灣鐵路股份有限公司. (2024). 臺鐵每日各站點進出站人數. 政府資料開放平臺. https://data.gov.tw/dataset/8792
• 國營臺灣鐵路股份有限公司. (2024). 臺鐵每日各站點進出站人數. 交通部政府資料開放專區. https://www.motc.gov.tw/201506260001/app/govdata_list/view?module=&id=1615&uid=201705110158
• 國營臺灣鐵路股份有限公司. (2024). 臺鐵全線剩餘票. 政府資料開放平臺. https://data.gov.tw/dataset/37933
• Law, A. M., & Kelton, W. D. (2007). Simulation modeling and analysis (4th ed.). McGraw-Hill.
• Wang, C.-L. (2024). AM 609 Simulation Study. Lecture Note. National Dong Hwa University. https://sys.ndhu.edu.tw/RD/TeacherTreasury/tlist.aspx?tcher=19
• Larson, R. C., & Odoni, A. R. (1981). Urban operation research. Massachusetts Institute of Technology. https://web.mit.edu/urban_or_book/www/book/index.html