主成分分析（PCA）

封面圖片為 ChatGPT 生成的主成分分析圖片，提示詞為： “A detailed 2D scatter plot illustrating Principal Component Analysis (PCA). The data points are grouped into multiple clusters with different colors, representing various categories. The X and Y axes are labeled ‘PC1’ and ‘PC2’, with grid lines for reference. A semi-transparent convex hull encases each cluster to emphasize grouping. The background is clean white with subtle shadows. The title ‘PCA Visualization’ is prominently displayed at the top.” 。

前言

主成分分析（Principal Component Analysis, PCA）是常見的降維（dimension reduction）方法，是將原先線性相依（linearly dependent）的資料集經由正交轉換（orthogonal transformation）後變成若干個線性獨立（linearly independent）的新變數表示的資料，使資料集經投影到新變數上損失的資訊量最小，並依新變數的變異數（variance）大小依次稱為第一主成分、第二主成分等。 PCA 常用於將高維度的資料映射到低維度空間，同時盡可能在降維過程中保留原始資料的重要特徵與訊息。

PCA 原理：最大可分性和最近重構性

PCA 透過最大可分性和最近重構性兩種思路將資料集優化。其中，最大可分性指的是樣本投影到低維空間時，每一個投影點間的距離都能盡量分開；而最近重構性則是指每一個樣本點到其投影點的距離平方和要足夠小，就如同迴歸（regression）中的最小平方法（least squares method）。

範例一

假設存在以下資料點： $$ \mathbf{X} = (X_1, X_2, \cdots, X_p)^\top, $$ 其中， $X_j = (x_{1j}, x_{2j}, \cdots, x_{nj})$ ， $i = 1, \cdots, n$ ， $j = 1, \cdots, p$ ， $\mathbf{X} \in \mathbb{R}^{n \times p}$ 。

最大可分性

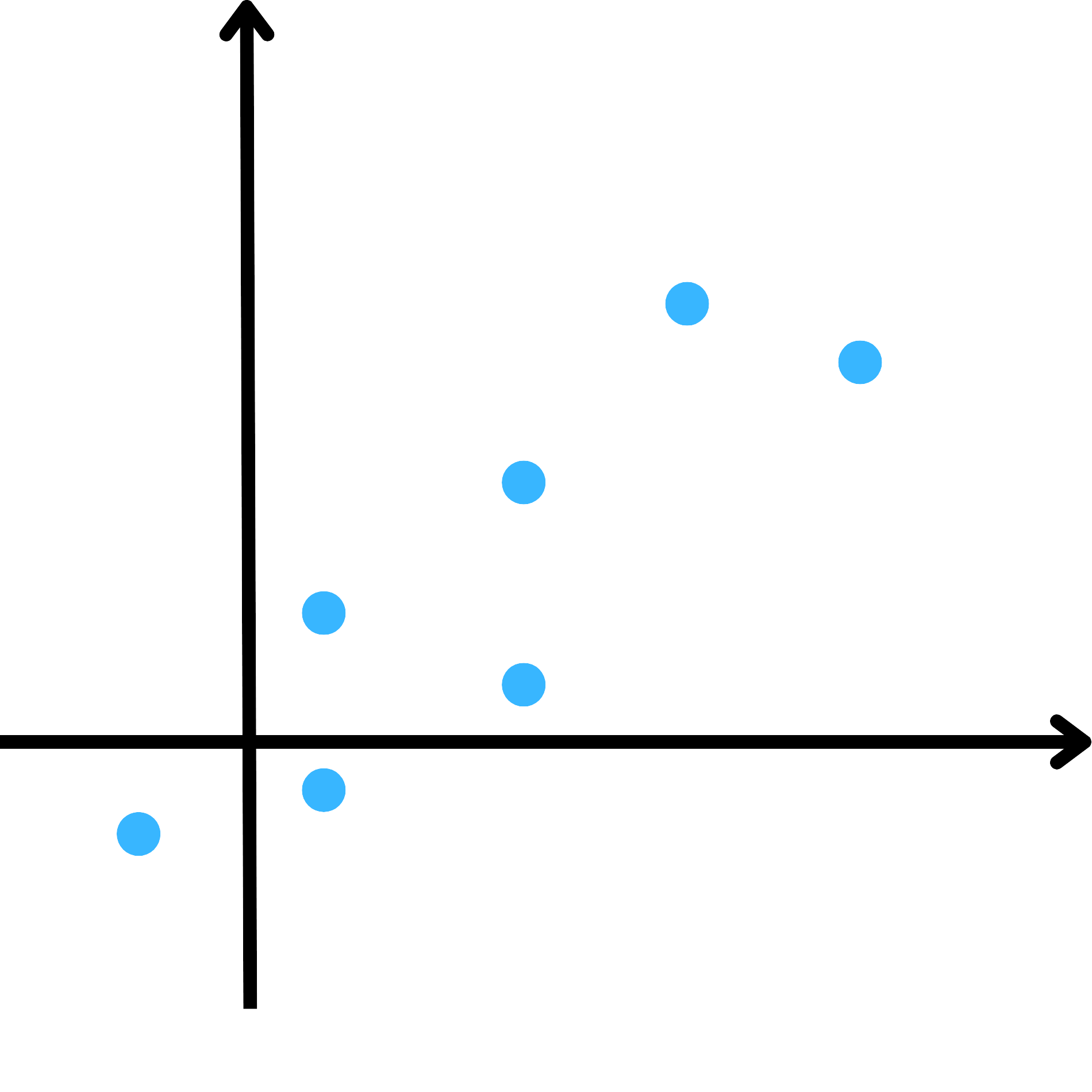
從範例一的資料點，我們可以繪製 M 、 N 線段如下。

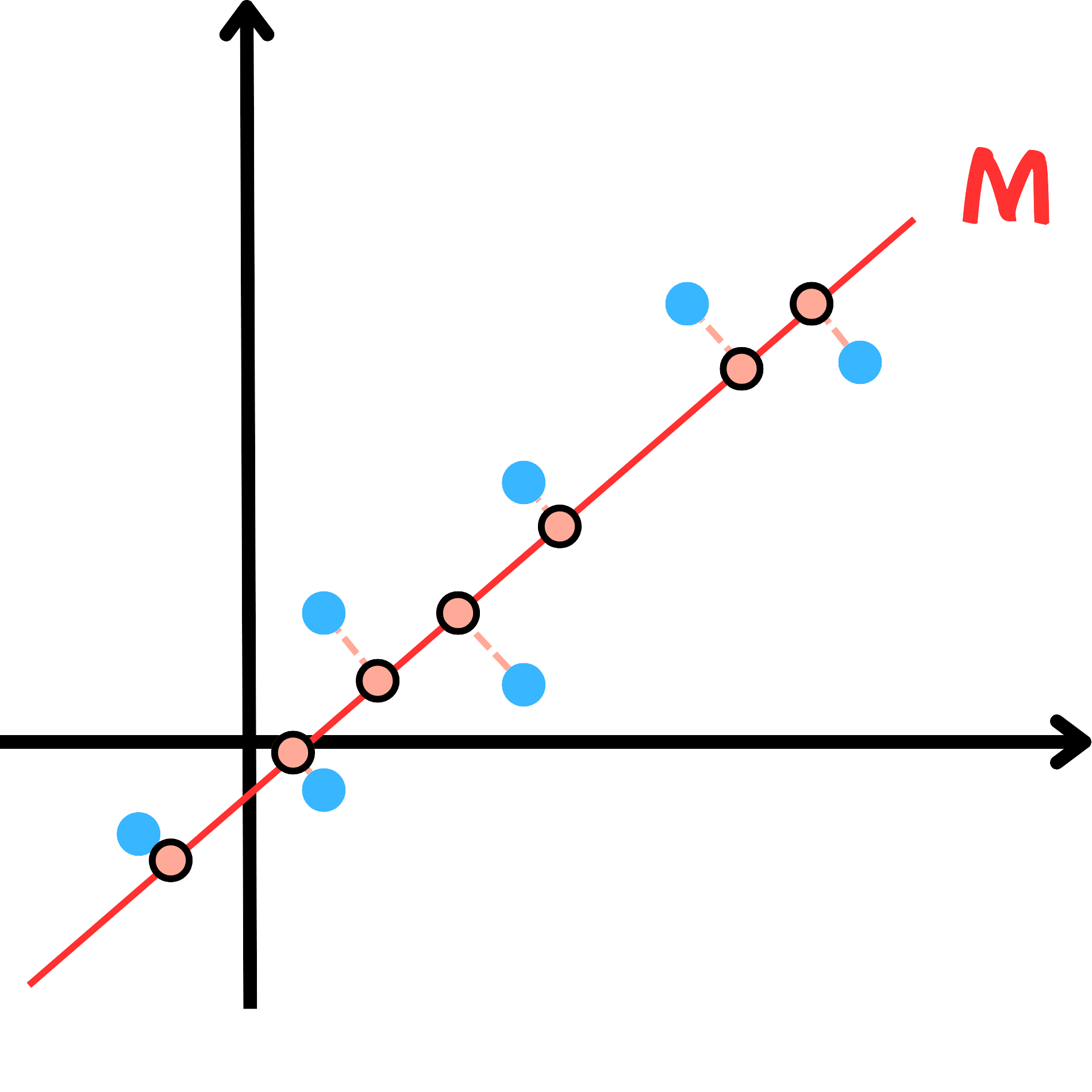
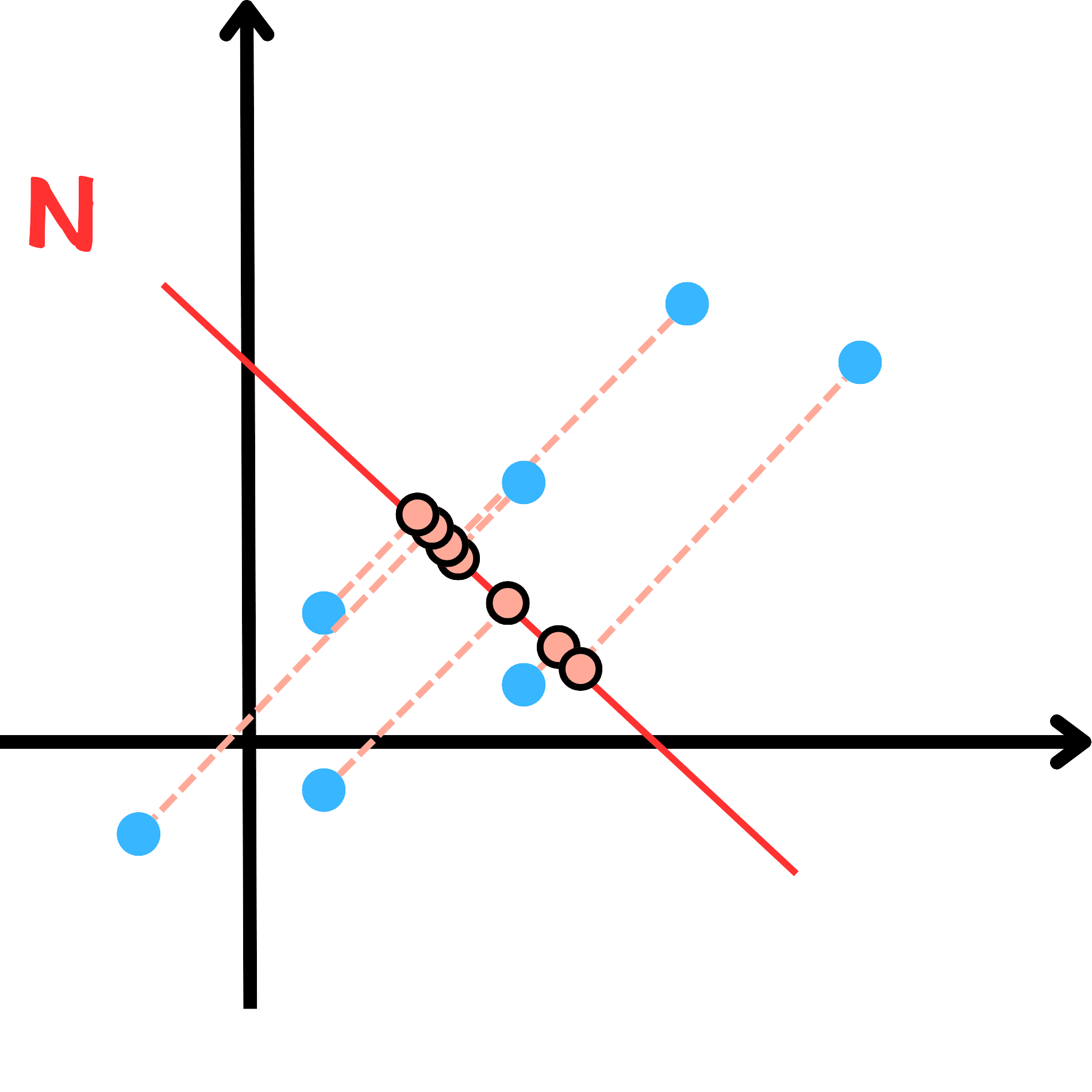
從以上資料點我們可以發現，資料點投影到 M 線段較投影到 N 線段分散，可以保留較多的資訊。若以統計角度說明，則可表達：各資料點在變數 M 上的變異數和較在變數 N 上的變異數和大。因此，我們會偏向選擇變異數和較大的變數作為第一主成分（PC1），例如範例一中的變數 M ，次之為第二主成分（PC2），並以此類推。

最近重構性

從最大可分性中繪製的 M 線段與 N 線段，我們也可以觀察到 M 線段中資料點與其投影點的距離平方和相較於 N 線段小。而我們通常會優先選擇投影距離平方和較小的變數作為第一主成分，也就是投影誤差（原始點與投影點的歐幾里得距離平方和）最小的變數為第一主成分，並以此類推。

由畢氏定理，我們知道在資料中心點固定的情況下，資料點與中心點的距離相同，則對於任意線段，投影距離愈長則投影點到資料中心點的距離愈短，投影距離愈短則投影點到資料中心點的距離愈長，即 PCA 選擇的方向同時最大化變異數並最小化投影誤差，因此最大可分性與最近重構性本質上是等價的。

中心化

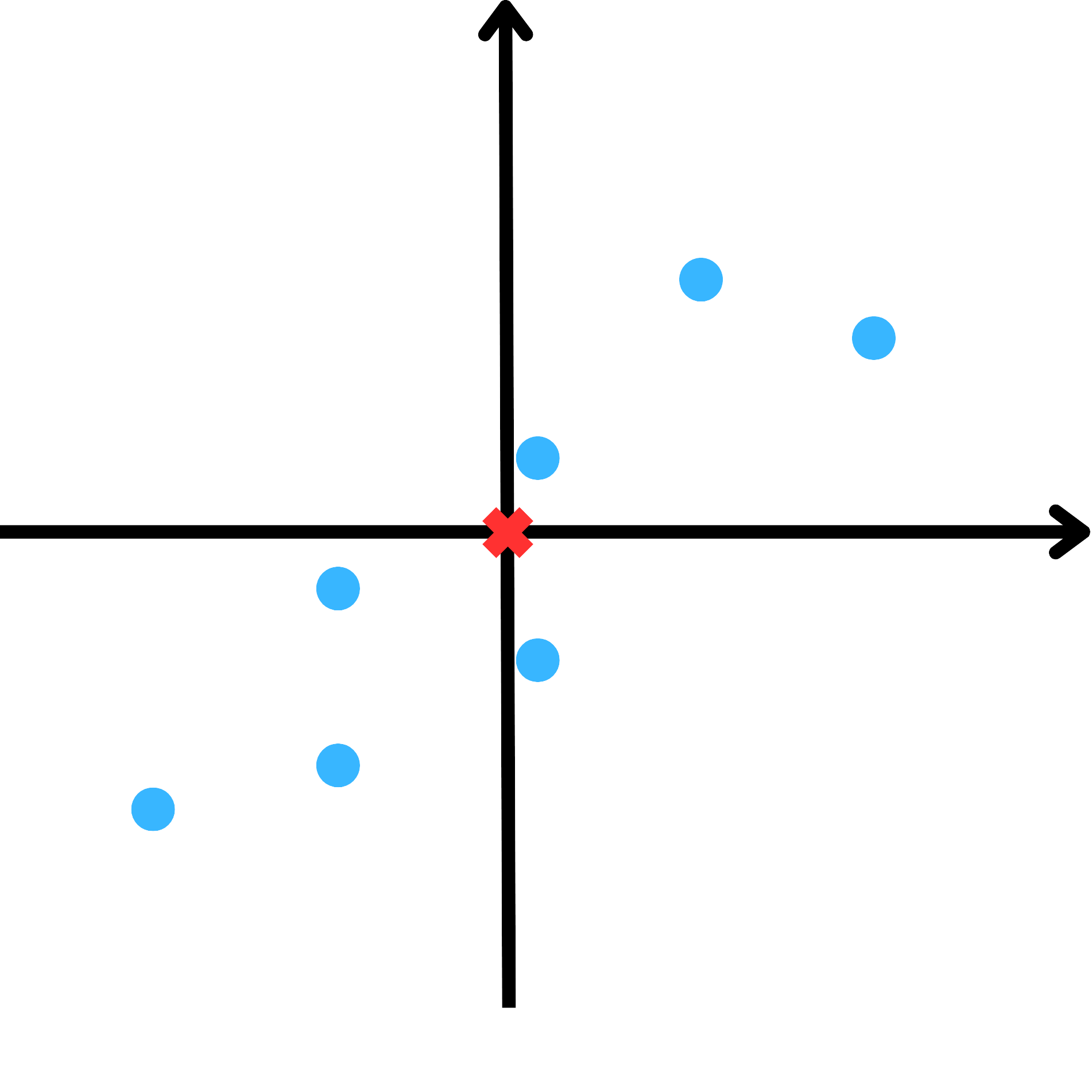
中心化讓資料改以坐標原點為中心，且不影響資料的分布情況。為方便正交轉換以及簡化矩陣運算過程，我們會在計算 PCA 的過程中進行中心化。

簡單來說，假設資料點同範例一一樣，我們可以選取各資料點平均並算出原資料中心點。

假設 $\overline{x}_j$ 為 $X_j$ 的平均值，則

$$ \overline{x}_j = \frac{1}{n} \sum_{i = 1}^n x_{ij}, \quad j = 1, \cdots, p, $$

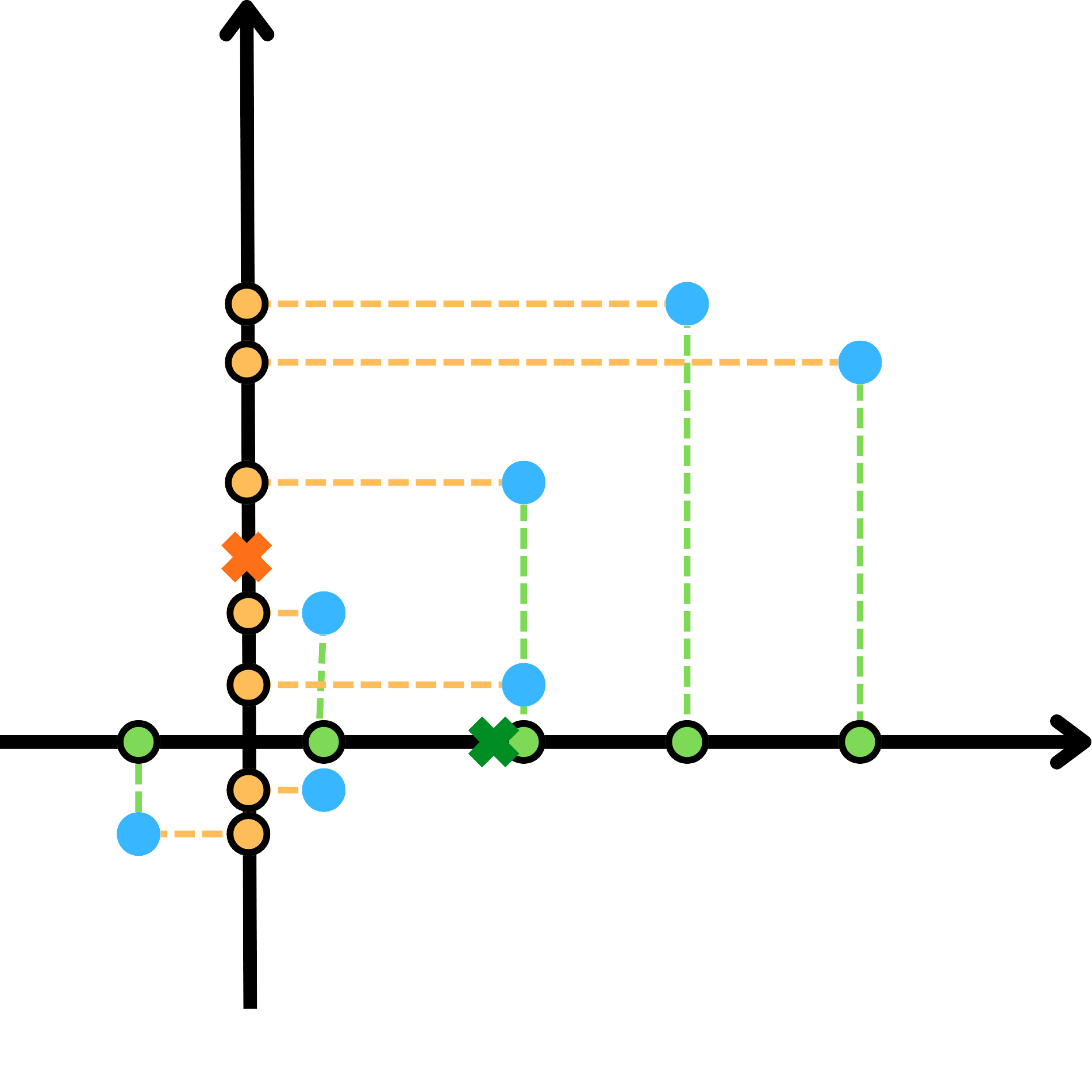
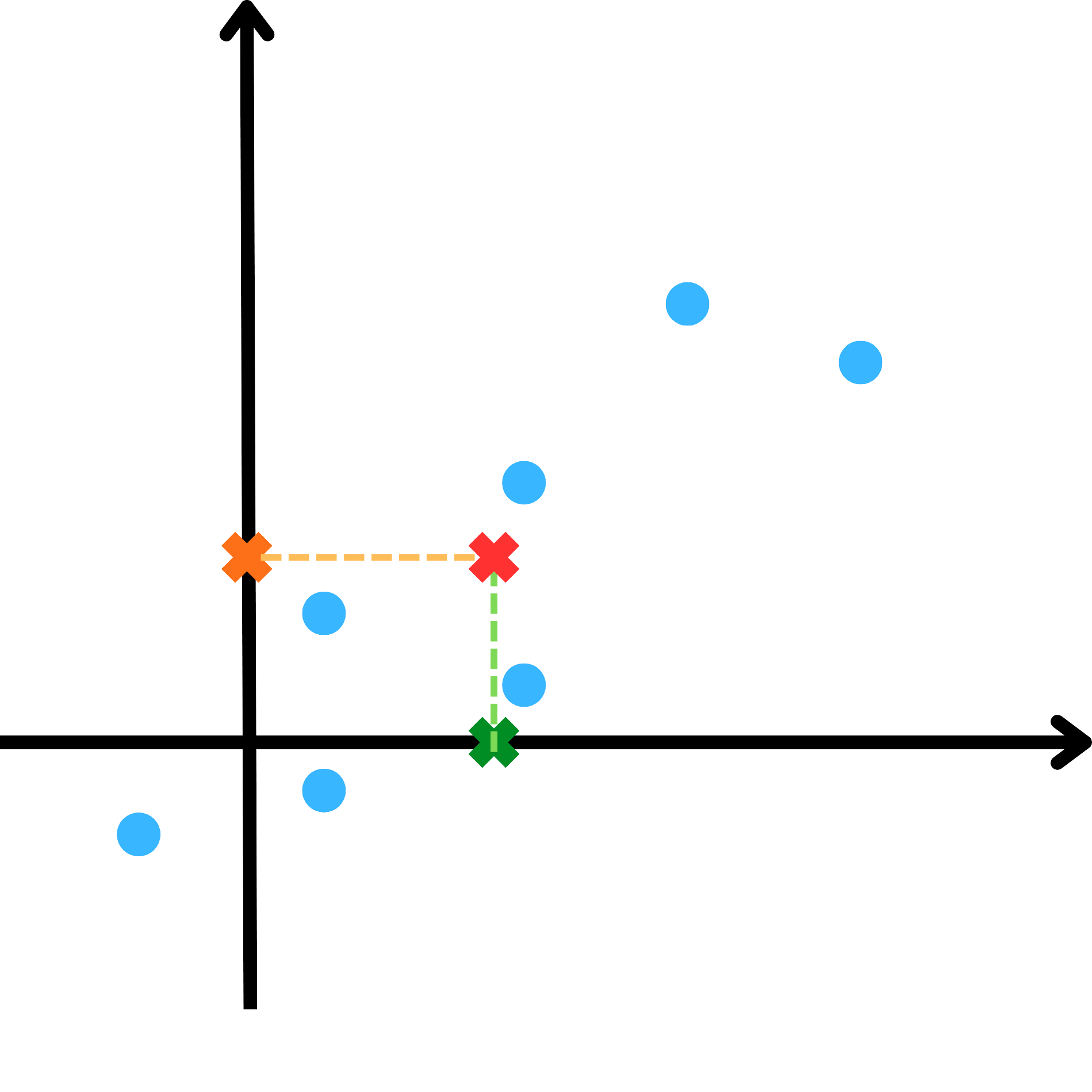
並原矩陣減去其平均值即可獲得中心化後的新矩陣（將資料中心點平移至原點處）。

$$ \mathbf{X}_c = \mathbf{X} - \overline{\mathbf{X}} = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{pmatrix} - \begin{pmatrix} \overline{x}_1 & \overline{x}_2 & \cdots & \overline{x}_p \\ \overline{x}_1 & \overline{x}_2 & \cdots & \overline{x}_p \\ \vdots & \vdots & \ddots & \vdots \\ \overline{x}_1 & \overline{x}_2 & \cdots & \overline{x}_p \end{pmatrix} $$

標準化

標準化（standardization）是為了消除不同資料間因尺度等因素而對結果產生的影響，並使各資料可在相同標準下（平均值為 0 ，標準差為 1 ）被檢視、提供參考價值。標準化的流程與中心化類似，但增加了除以標準差這一步。與中心化相同的是，標準化後的資料集仍擁有與原資料即相同的排序、分布情況，一般在進行資料預處理時都會先進行中心化再考慮是否需要進行標準化。

我們也可以對範例一中的資料點進行標準化。假設 $\sigma^2_j$ 為 $X_j$ 的變異數，由變異數的定義我們可寫下：

$$ \sigma^2_j = \frac{1}{n} \sum_{i = 1}^n (x_{ij} - \overline{x}_j)^2, \quad j = 1, \cdots, p, $$

因此，將資料集標準化的結果為

$$ \mathbf{Z} = \frac{\mathbf{X}_c}{\mathbf{\sigma}} = \frac{\mathbf{X}-\overline{\mathbf{X}}}{\mathbf{\sigma}}, $$

其中

$$ \mathbf{\sigma} = \begin{pmatrix} \sigma_1 & \sigma_1 & \cdots & \sigma_1 \\ \sigma_2 & \sigma_2 & \cdots & \sigma_2 \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_p & \sigma_p & \cdots & \sigma_p \end{pmatrix}. $$

資料點投影

經過中心化、標準化等資料預處理方法後，接下來要將資料點投影到新變數上。

假設現有資料向量 $x_i$ ，現在我們想將 $x_i$ 投影到 $v$ 上，稱為 $w$ 。則由投影夾角 $\theta$ ，我們可以知道 $w$ 的長度為 $\|x_i\| \|v\| \cos(\theta)$ ，其中 $\|x_i\|$ 表示 $x_i$ 的長度。若 $v$ 為單位向量（unit vector），則 $w$ 的長度可改寫為 $\|x_i\| \cos(\theta)$ 。

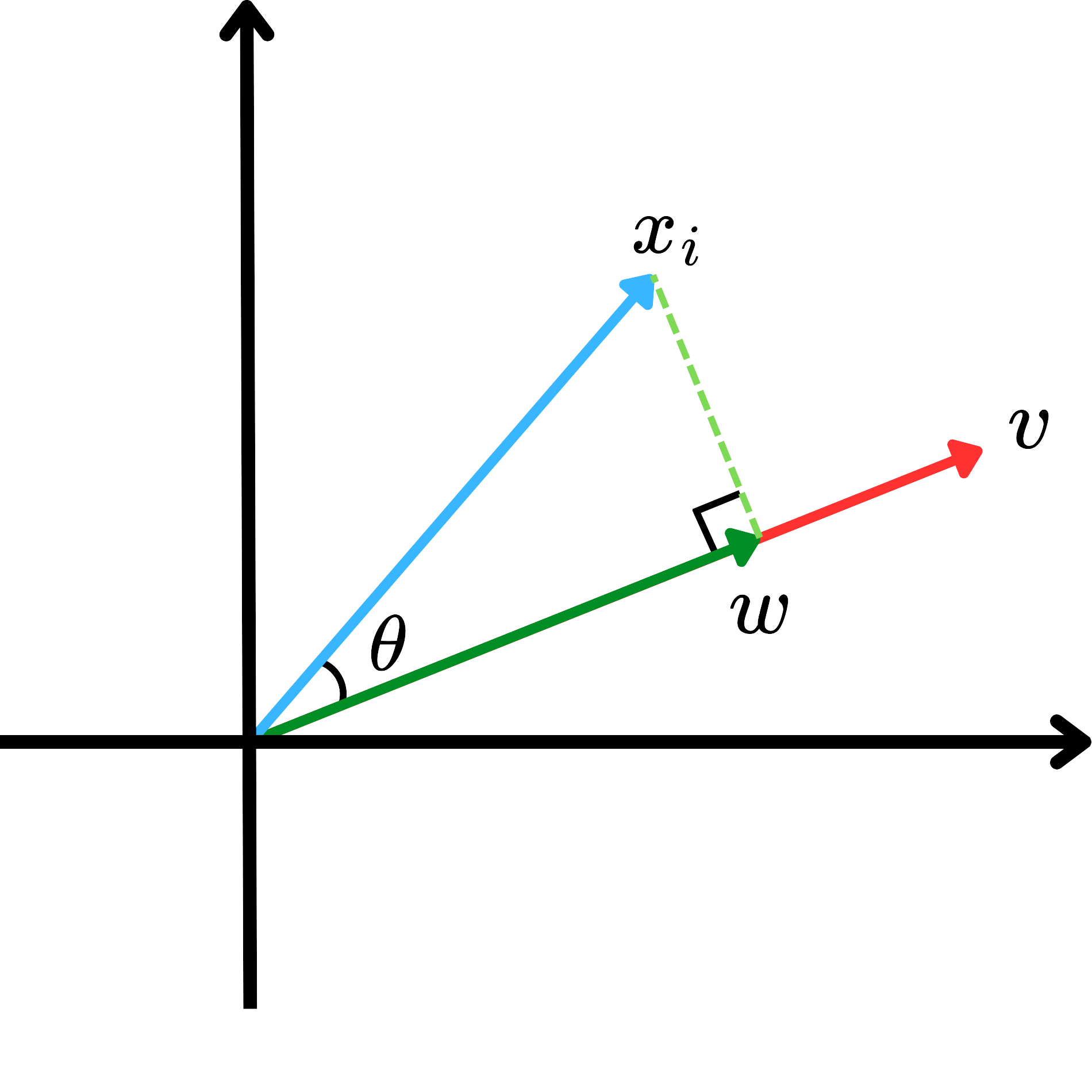
以上為單個資料點的投影公式。

現在考慮資料集中多資料點的投影。假設使用範例一中的資料點 $\mathbf{X} = (X_1, X_2, \cdots, X_p)^\top$ ，其中 $X_j = (x_{1j}, x_{2j}, \cdots, x_{nj})$ 。令 $\mathbf{\delta} = (\delta_1, \delta_2, \cdots, \delta_p)^\top$ 是 $\mathbf{X}$ 的投影方向（主成分向量），則所有資料點的投影可寫成

$$ \mathbf{\mathcal{P}} = \mathbf{\delta}^\top \mathbf{X} = (\delta_1, \delta_2, \cdots, \delta_p) \begin{pmatrix} X_1 \\ X_2 \\ \vdots \\ X_p \end{pmatrix} = \sum_{j=1}^p \delta_j X_j, $$

$\mathbf{\mathcal{P}} = (\mathcal{P}_1, \mathcal{P}_2, \cdots, \mathcal{P}_p)^\top$ 。其中 ${\delta}$ 要符合 $\sum_{j=1}^p \delta_j^2 = 1$ 用以保證投影到的向量為單位向量。

變異數計算

那我們要怎麼找到適合的投影方向 $\mathcal{P}_i$ ，使得我們在該投影向量上擁有最大可分性呢？已知以下條件

$$ \max_{\{\delta:\|\delta\| = 1\}} Var(\mathbf{\mathcal{P}}) = \max_{\{\delta:\|\delta\| = 1\}} Var(\mathbf{\delta}^\top \mathbf{X}) = \max_{\{\delta:\|\delta\| = 1\}} \mathbf{\delta}^\top Var(\mathbf{X}) \mathbf{\delta}, $$

為了找到最大的變異數，我們必須先找到適合的 $\mathbf{\delta}$ 。在此之前，我們需要先知道以下定理：

根據以上定理，我們可以知道投影方向 $\mathbf{\delta}$ 可由共變異矩陣（covariance matrix） $\Sigma = Var(\mathbf{X}) \in \mathbb{R}^{p \times p}$ 中最大的特徵值 $\lambda_1$ 所對應的特徵向量（eigenvector） $\gamma_1$ 給定。

主成分分析

第一主成分

回到一開始的例子，假設範例一中的資料點 $\mathbf{X}$，從變異數計算中所提到的定理，我們可以知道第一主成分（first principal component, PC1）為

$$ Y_1 = \gamma_1^\top \mathbf{X}, $$

且 $Y_1 \in \mathbb{R}^p$ 擁有投影後最大的變異數 $$ \argmax_{\{\gamma_1:\|\gamma_1\| = 1\}} \mathbf{\gamma_1}^\top Var(\mathbf{X}) \mathbf{\gamma_1}, $$

即 $\gamma_1$ 滿足

$$ \Sigma \gamma_1 = \lambda_1 \gamma_1. $$

由資料集 $\mathbf{X}$ ，我們可知 $E(\mathbf{X}) = \overline{\mathbf{X}}$ ，且 $Var(\mathbf{X}) = \Sigma$ 。將共變異矩陣 $\Sigma$ 對角化（diagonalization）可得

$$ \Sigma = \Gamma \Lambda \Gamma^\top, $$

因此，我們也可得 PC1 為

$$ Y_1 = \Gamma^\top_1 (\mathbf{X}-\overline{\mathbf{X}}) = \Gamma^\top_1 \mathbf{X}_{c} \in \mathbb{R}^n. $$

第二主成分

現在我們已經得出 PC1 $Y_1$ 與其投影向量 $\mathcal{P}_1$ 。類似地，我們可以用相同的方法找出第二主成分（second principal component, PC2）。需要注意的是，PC2 的投影向量需與 PC1 垂直，換句話說

$$ \mathcal{P}_2^\top \mathcal{P}_1 = 0, $$

而 PC2 的變異數為

$$ \argmax_{\left\{\gamma_2:\|\gamma_2\| = 1, \gamma_2^\top \gamma_1 = 0 \right\}} \mathbf{\gamma_2}^\top Var(\mathbf{X}) \mathbf{\gamma_2}. $$

若 $\gamma_2$ 符合以上條件，即可稱為 PC2

$$ Y_2 = \Gamma^\top_2 (\mathbf{X}-\overline{\mathbf{X}}) = \Gamma^\top_2 \mathbf{X}_{c} \in \mathbb{R}^n. $$

其他主成分

總結以上，對於第 $q$ 主成分，我們會有

$$ Y_q = \Gamma^\top_q (\mathbf{X}-\overline{\mathbf{X}}) = \Gamma^\top_q \mathbf{X}_{c} \in \mathbb{R}^n, $$

且其投影向量 $\mathcal{P}_q$ 必與 $\mathcal{P}_{q-1}$ 垂直（ $\mathcal{P}_q^\top \mathcal{P}_{q-1} = 0$ ），主成分總數量不超過資料集的特徵數量 $p$ 維度。

對於主成分 $\mathbf{Y} = \Gamma^\top \mathbf{X}_{c}$，存在以下特性：

Python 範例

資料集簡介

本次使用的資料集為 Boston housing data ，這是關於美國麻薩諸塞州首府——波士頓 1978 年的房價資料，該資料集包含波士頓都市區每個人口普查區的 506 個觀察值。

變數說明

由 Applied Multivariate Statistical Analysis 這本書，我們可以知道此資料集共 506 筆資料， 14 個變數。每個變數說明如下：

資料集

以下使用 Python 作為分析 PCA 的語言。

1
2
3
4
5
6
7
8
9

import pandas as pd

# 讀取檔案
file_path = "bostonh.dat"
df = pd.read_csv(file_path, sep = r"\s+", header = None)  # r"\s+" 表示以一個或多個空格分隔
df.columns = [f"X{i+1}" for i in range(df.shape[1])]

# 檢視資料集
print(df.head())

資料集部分資訊如下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

        X1    X2    X3  X4     X5     X6    X7      X8  X9    X10   X11  \
0  0.00632  18.0  2.31   0  0.538  6.575  65.2  4.0900   1  296.0  15.3   
1  0.02731   0.0  7.07   0  0.469  6.421  78.9  4.9671   2  242.0  17.8   
2  0.02729   0.0  7.07   0  0.469  7.185  61.1  4.9671   2  242.0  17.8   
3  0.03237   0.0  2.18   0  0.458  6.998  45.8  6.0622   3  222.0  18.7   
4  0.06905   0.0  2.18   0  0.458  7.147  54.2  6.0622   3  222.0  18.7   

      X12   X13   X14  
0  396.90  4.98  24.0  
1  396.90  9.14  21.6  
2  392.83  4.03  34.7  
3  394.63  2.94  33.4  
4  396.90  5.33  36.2  

同時使用以下程式碼檢視資料及是否有缺值。

1

print(f"NAs:\n{df.isna().sum()}")

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

NAs:
X1     0
X2     0
X3     0
X4     0
X5     0
X6     0
X7     0
X8     0
X9     0
X10    0
X11    0
X12    0
X13    0
X14    0
dtype: int64

從以上結果可知，此資料集不存在缺值。

定義變數與標準化

接下來，我們定義特徵變數 x 與目標變數 y 。藉由定義特徵變數和目標變數，後續完成 PCA 後可將結果（PC）再使用其它模型進行分析，如隨機森林等。如果僅需要進行 PCA ，可以只將全部變數都定義為特徵變數。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 定義特徵變數和目標變數
x = df.drop("X14", axis = 1)  # 定義房價以外為特徵變數
y = df["X14"]  # 定義房價為目標變數

# 標準化
scaler = StandardScaler()
x_scaled = pd.DataFrame(scaler.fit_transform(x), columns = x.columns, index=x.index)

PCA

接下來，我們將進行主成分分析。在這邊，我們使用 scikit-learn 的 PCA() 函數，而 PCA() 函數也可以使用 n_components 參數決定要保留多少變異數。此處不填寫n_components 參數，表示保留全部參數（最大變異數）。

1
2
3
4
5
6
7

pca = PCA()  # 保留全部 PC
#pca = PCA(n_components = 0.95)  # 設定保留 95% 的變異數

print(f"降維前的資料形狀: {x_scaled.shape}")
x_reduced = pd.DataFrame(pca.fit_transform(x_scaled), index = x.index)
print(f"降維後的資料形狀: {x_reduced.shape}")
print(f"選擇的主成分數量: {pca.n_components_}")

1
2
3

降維前的資料形狀: (506, 13)
降維後的資料形狀: (506, 13)
選擇的主成分數量: 13

此處我們也能直觀的看到主成分總數量不超過資料集的特徵數量。

接下來，我們輸出 PCA 的成分矩陣與變異量，並輸出成 data frame 方便查看。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

# 建立 PCA 成分的 DataFrame，加入變異量與最重要變數
pca_components_df = pd.DataFrame(
    pca.components_,  # PCA 成分矩陣
    columns = x.columns,  # 原始特徵名稱
    index = [f"PC{i+1}" for i in range(pca.n_components_)]  # 命名 PCA 主成分
)

# 計算變異量（Explained Variance）
pca_components_df["Explained Variance"] = pca.explained_variance_ratio_

# 計算累積變異量（Cumulative Explained Variance）
pca_components_df["Cumulative Explained Variance"] = pca.explained_variance_ratio_.cumsum()

# 找出每個 PCA 主成分最重要的變數（權重絕對值最大的變數）
pca_components_df["Most Important Feature"] = pca_components_df.iloc[:, :-3].abs().idxmax(axis = 1)

# 顯示結果
print(pca_components_df)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

            X1        X2        X3        X4        X5        X6        X7  \
PC1   0.250951 -0.256315  0.346672  0.005042  0.342852 -0.189243  0.313671   
PC2  -0.315252 -0.323313  0.112493  0.454829  0.219116  0.149332  0.311978   
PC3   0.246566  0.295858 -0.015946  0.289781  0.120964  0.593961 -0.017675   
PC4   0.061771  0.128712  0.017146  0.815941 -0.128226 -0.280592 -0.175206   
PC5  -0.082157 -0.320617  0.007811 -0.086531 -0.136854  0.423447 -0.016691   
PC6   0.219660  0.323388  0.076138 -0.167490  0.152983 -0.059267  0.071709   
PC7   0.777607 -0.274996 -0.339576  0.074136 -0.199635  0.063940  0.116011   
PC8  -0.153350  0.402680 -0.173932  0.024662 -0.080121  0.326752  0.600823   
PC9   0.260390  0.358137  0.644416 -0.013728 -0.018522  0.047898 -0.067562   
PC10 -0.019369 -0.267527  0.363532  0.006182 -0.231056  0.431420 -0.362779   
PC11  0.109644 -0.262756  0.303169 -0.013927 -0.111319 -0.053162  0.459159   
PC12  0.086761 -0.071425 -0.113200 -0.003983  0.804323  0.152873 -0.211936   
PC13  0.045952 -0.080919 -0.251077  0.035922  0.043630  0.045567 -0.038551   

            X8        X9       X10       X11       X12       X13  \
PC1  -0.321544  0.319793  0.338469  0.204942 -0.202973  0.309760   
PC2  -0.349070 -0.271521 -0.239454 -0.305897  0.238559 -0.074322   
PC3  -0.049736  0.287255  0.220744 -0.323446 -0.300146 -0.267000   
PC4   0.215436  0.132350  0.103335  0.282622  0.168498  0.069414   
PC5  -0.098592  0.204132  0.130461  0.584002  0.345607 -0.394561   
PC6  -0.023439  0.143194  0.192934 -0.273153  0.803455  0.053216   
PC7  -0.103900 -0.137943 -0.314887  0.002324  0.070295  0.087011   
PC8   0.121812 -0.080358 -0.082774  0.317884  0.004923  0.424353   
PC9  -0.153291 -0.470891 -0.176563  0.254428 -0.044898 -0.195221   
PC10  0.171213 -0.021909  0.035168 -0.153430  0.096515  0.600711   
PC11  0.695693 -0.036544  0.104836 -0.174505 -0.019275 -0.271382   
PC12  0.390941 -0.107026 -0.215191  0.209599  0.041723  0.055226   
PC13 -0.018299 -0.633490  0.720233  0.023398 -0.004463  0.024432   

      Explained Variance  Cumulative Explained Variance Most Important Feature  
PC1             0.471296                       0.471296                     X3  
PC2             0.110252                       0.581548                     X4  
PC3             0.095586                       0.677134                     X6  
PC4             0.065967                       0.743101                     X4  
PC5             0.064217                       0.807318                    X11  
PC6             0.050570                       0.857888                    X12  
PC7             0.041181                       0.899069                     X1  
PC8             0.030469                       0.929538                     X7  
PC9             0.021303                       0.950841                     X3  
PC10            0.016941                       0.967783                     X6  
PC11            0.014309                       0.982091                     X8  
PC12            0.013023                       0.995115                     X5  
PC13            0.004885                       1.000000                    X10

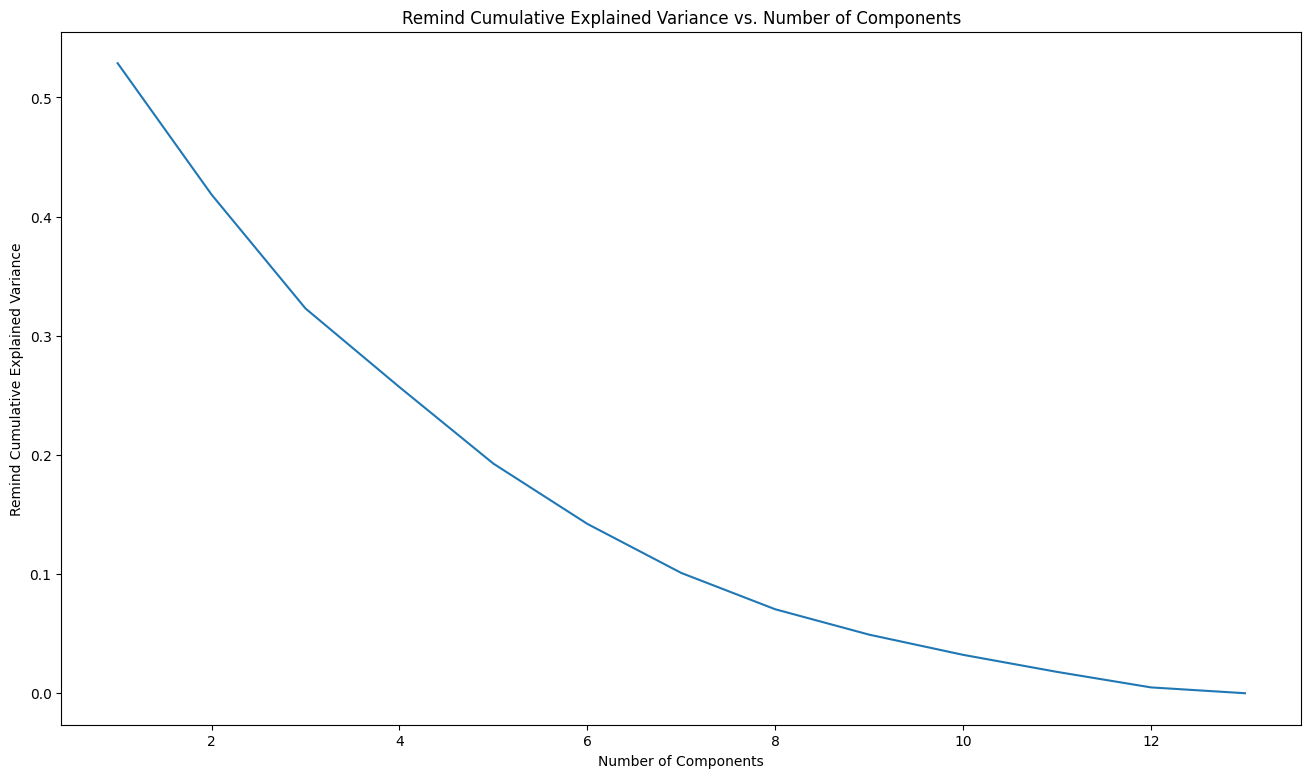
從以上結果我們可以觀察到， PC1 的解釋變異量為 PC2 的 4 倍，可見 PC1 在解釋資料集變異性方面的主導地位。進一步觀察累計解釋變異量（Cumulative Explained Variance），我們發現隨著主成分的增加，解釋的變異量累積速度變慢。這讓我們能夠有依據地決定在降維後保留多少主成分，達到讓資料集有效解釋，但又能避免過多的維度帶來的冗餘資訊和計算負擔。因此，根據這些結果，我們可以選擇保留前幾個主要的主成分來有效地解釋資料，而不必保留所有的主成分。

以下繪製剩餘累積變異量圖，讓我們能更直觀的觀察剩餘累積變異量，並決定要保留的主成分數量。

使用以下程式碼能找出所有經主成分轉換（PC transformation）後的點

1
2
3
4
5

# 找出 PC 所有的點
pc_df = pd.DataFrame()
for i in range(pca.components_.shape[0]):
    pc_df[f"PC{i+1}"] = x.values @ pca.components_[i]
print(pc_df.head())

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

         PC1        PC2        PC3        PC4         PC5         PC6  \
0  38.890181  32.935324 -51.873961  92.167019  178.427648  382.499065   
1  33.023432  54.798669 -71.207997  83.321389  176.841195  367.268772   
2  26.538735  48.768409 -67.853639  85.185186  178.071394  362.405072   
3  12.756987  47.783518 -72.338822  86.619758  177.275189  358.347339   
4  15.652406  50.778719 -73.709208  85.656877  177.036592  360.899950   

         PC7        PC8        PC9       PC10       PC11       PC12  \
0 -63.253078  32.971896 -64.423458  25.122328  47.667764 -56.089807   
1 -41.167341  40.135316 -59.975715  26.991812  53.496420 -45.713799   
2 -43.914223  27.501830 -57.556203  30.316431  46.747978 -42.276562   
3 -37.954676  20.639702 -56.427659  32.854127  36.984715 -33.688927   
4 -36.574611  26.755055 -57.546991  31.525144  40.145396 -35.216528   

         PC13  
0  206.962371  
1  167.304566  
2  167.918899  
3  154.655918  
4  154.388828  

PC1 小提琴圖

我們可以使用小提琴圖查看 PC1 資料的分布情況。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

import plotly.express as px

fig = px.violin(pc_df,
                 y = "PC1", 
                 title = "PC1 violin plot",
                 labels = {"PC1": "PC1"},
                 points = "all",
                 box = True  # 顯示四分位數
                 )

fig.update_traces(
    box_width = 0.1  # 控制四分位數框的寬度，讓框小一點
)

fig.update_layout(
    width = 1200,  # 設定寬度
    height = 600,  # 設定高度
)

fig.write_html("PC1 violin plot.html")
fig.show()

若無法查看互動式 PC1 小提琴圖，或是需要全螢幕檢視，請點此處前往。

PC1 與 PC2 散佈圖

我們可以使用散佈圖查看 PC1 與 PC2 資料的分布情況。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

import plotly.express as px
fig = px.scatter(pc_df,
                 x = "PC1", 
                 y = "PC2", 
                 title = "PC1 and PC2 scatter plot",
                 labels = {"PC1": "PC1", "PC2": "PC2"}
                 )

fig.update_layout(
    width = 600,  # 設定寬度
    height = 600,  # 設定高度
)

fig.write_html("PC1 and PC2 scatter plot.html")
fig.show()

若無法查看互動式 PC1 與 PC2 散佈圖，或是需要全螢幕檢視，請點此處前往。

結語

PCA 是一個實用的降維方法，能將資料集從複雜的 $p$ 維度在盡可能保留資訊的情況映射到 $q$ 維度空間。使用 PCA 有助於減少資料的維度，從而降低計算和儲存成本，並提高模型的效率與準確性。通過去除不必要的噪音和特徵間的相關性，PCA 能夠改善機器學習模型的泛化能力，並且使得資料更具可解釋性。

運行環境

• 作業系統：Windows 11 24H2
• 程式語言：Python 3.12.9

延伸學習

• 本文使用的 ipynb 檔案。

參見

• 資料集探索與分析

參考資料

• Wolfgang karl härdle 和 léopold simar（2015年）。Applied Multivariate Statistical Analysis（第四版）。Springer。https://link.springer.com/book/10.1007/978-3-662-45171-7

• 动画讲编程。（2022年8月2日）。机器学习，什么是PCA降维？一个动画告诉你答案 [影片]。YouTube。2025年3月25日參考自https://youtu.be/FI0H_HStNJU

• Tommy Huang。（2018年4月20日）。機器/統計學習:主成分分析(Principal Component Analysis, PCA)。2025年3月25日參考自https://chih-sheng-huang821.medium.com/機器-統計學習-主成分分析-principle-component-analysis-pca-58229cd26e71

• 李錦州。（2024年1月27日）。主成分分析 (Principal Component Analysis, PCA)。2025年3月25日參考自https://jinzhou.netlify.app/posts/principal-component-analysis/

• Quantnet。（2025年1月27日）。 MVA。Github。https://github.com/QuantLet/MVA

• Violin Plots in Python。（無日期）。Plotly|Graphing Libraries。2025年4月1日參考自https://plotly.com/python/violin/

• 李航（2022）。機器學習聖經：最完整的統計學習方法（初版）。深智數位股份有限公司。