兩隨機變數相加後的變異數證明

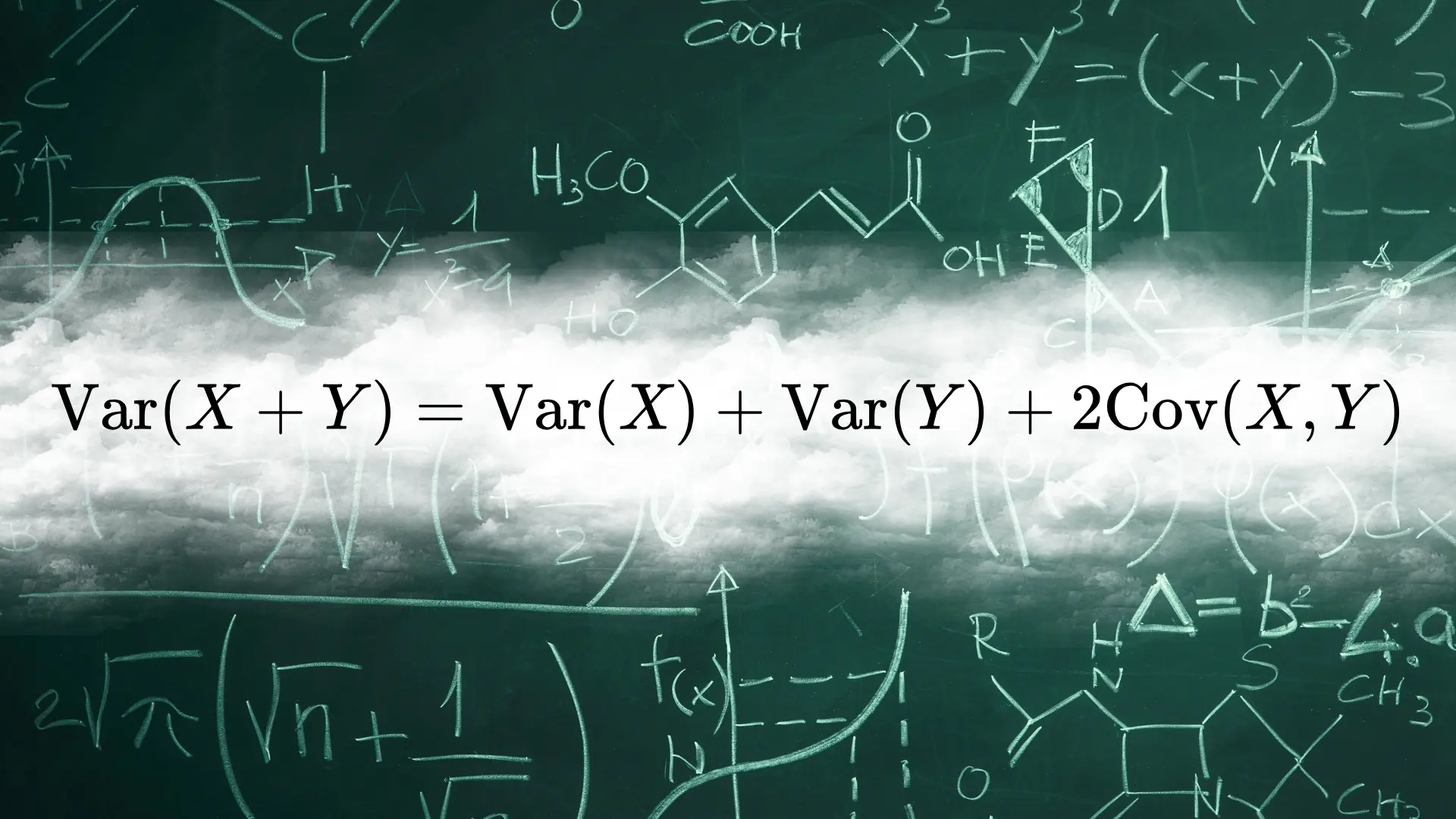
這是一個經典的數理統計學證明，也就是兩隨機變數和的變異數，是否會等於兩變數各自變異數的和。

其定理與證明如下：

定理

證明

要證明此定理，我們得先了解變異數（variance）的定義。對於隨機變數 $X$ ，我們定義其變異數 $\text{Var} (X)$ 如下：

$$ \text{Var} (X) = \text{E} \left[ \left(X - \text{E} (X) \right)^2 \right] $$

其中， $\text{E} (X)$ 為 $X$ 的期望值（expected value）。而 $\text{E} (X)$ 定義如下：

• $X$ 是離散隨機變數（discrete random variable），且其定義域（domain）為 $\boldsymbol{X}$ 。 $$ \text{E} (X) = \sum_{x \in \boldsymbol{X}} x \cdot f_X (x) $$ 其中， $f_X(x)$ 是機率質量函數（probability mass function, pmf）。

• $X$ 是連續隨機變數（continuous random variable），且其定義域為 $\boldsymbol{X}$ 。 $$ \text{E} (X) = \int_{x \in \boldsymbol{X}} x \cdot f_X (x) dx $$ 其中， $f_X(x)$ 是機率密度函數（probability density function, pdf）。

同時，已知期望值 $\text{E}$ 是線性函數，且

$$ \text{E} (aX + bY) = a \text{E} (X) + b \text{E} (Y) $$

其中， $X$ 和 $Y$ 為同一機率空間中的兩個隨機變數， $a$ 和 $b$ 為任意實數。

而對於兩隨機變數 $X$ 和 $Y$ ，共變異數定義如下：

$$ \text{Cov} (X, Y) = \text{E} \left[ (X - \text{E} (X)) \cdot (Y - \text{E} (Y)) \right] $$

由前項定義，我們可以藉由分解 $\text{Var} (X + Y)$ 並得到：

$$ \begin{align*} \text{Var} (X + Y) & = \text{E} \left[ \left( (X + Y) - \text{E} (X + Y) \right)^2 \right] \\ & = \text{E} \left[ \left( X + Y - \text{E} (X) - \text{E} (Y) \right)^2 \right] \\ & = \text{E} \left[ \left( X - \text{E} (X) + Y - \text{E} (Y) \right)^2 \right] \\ & = \text{E} \left[ \left( (X - \text{E} (X)) + (Y - \text{E} (Y)) \right)^2 \right] \\ & = \text{E} \left[ (X - \text{E} (X))^2 + 2 \cdot (X - \text{E} (X)) \cdot (Y - \text{E} (Y)) + (Y - \text{E} (Y))^2 \right] \\ & = \text{E} \left[ (X - \text{E} (X))^2 \right] + 2 \cdot \text{E} \left[ (X - \text{E} (X)) \cdot (Y - \text{E} (Y)) \right] + \text{E} \left[ (Y - \text{E} (Y))^2 \right] \\ & = \text{Var} (X) + 2 \text{Cov} (X, Y) + \text{Var} (Y) \\ & = \text{Var} (X) + \text{Var} (Y) + 2 \text{Cov} (X, Y) \end{align*} $$

故得證。

獨立性

當兩隨機變數 $X$ 和 $Y$ 相互獨立時，其共變異數為 0 。證明如下：

由上述證明，我們也可知：

當 $X \mathrel{\perp\!\!\!\perp} Y$ 時， $\text{Cov} (X,Y)=0$ ，且

$$ \text{Var} (X + Y) = \text{Var} (X) + \text{Var} (Y) $$