直角坐標、極坐標與球坐標

Josh

發佈於 2025-06-08 更新於 2025-06-21 約 2074 字預計閱讀 5 分鐘次閱讀

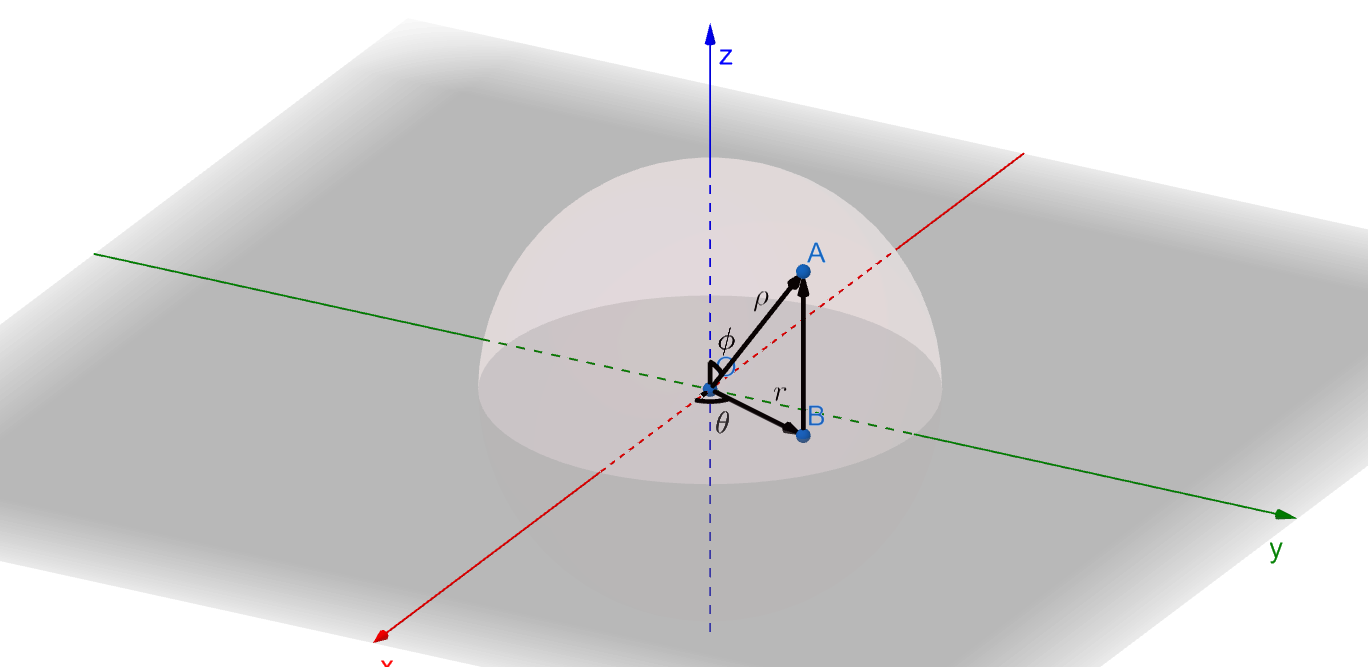
封面圖片是作者於 GeoGebra 製作的球坐標系介紹圖片，製於 2025 年 6 月 9 日。

前言

常見的坐標系包含直角坐標系、極坐標系與球坐標系，每一種坐標系各有其不同的使用情形與優缺點。

直角坐標系

直角坐標系（rectangular coordinate system）又稱為笛卡兒坐標系（Cartesian coordinate system），是由法國數學家勒內·笛卡兒（René Descartes）所引入的。

直角坐標系是由幾條相互垂直且相交於原點的坐標軸組成，且坐標系中的每個點均可以對應到所有坐標軸上。

二維坐標系

二維直角坐標系通常由 $x$ 軸與 $y$ 軸組成，其中 $x$ 軸又稱為橫軸， $y$ 軸又稱為縱軸，二維直角坐標平面又稱為 $xy$ 平面。在繪製二維直角坐標系時，需遵守以下準則：

$x$ 軸與 $y$ 軸需要相互垂直，而兩軸相交處稱為原點，並標記為 $\textit{O}$ 。
$x$ 軸右方為正方向，左方為負方向，也就是說數值愈靠近右邊則愈大，愈靠近左邊則愈小。
$y$ 軸上方為正方向，下方為負方向，也就是說數值愈靠近上方則愈大，愈靠近下方則愈小。
為了於直角坐標系上標示坐標，我們會於坐標系上每隔一個固定的單位長度就刻劃相對應的數值於坐標軸上。
二維直角坐標系的坐標點標記為 $(x, y)$ 。

三維坐標系

三維直角坐標系的組成方式與二維直角坐標系相似，但多出一個新的維度 $z$ 軸。同樣地，$x$ 軸、 $y$ 軸與 $z$ 軸會相互正交於原點，並以 $(x, y, z)$ 標記對應的坐標點。

極坐標系

極坐標系（polar coordinate system）是一種二維坐標系，提出並引入的人不詳。與直角坐標系不同的是，極坐標的標示方法為坐標點與原點的距離 $r$ 以及與極軸 $L$ 的角度 $\theta$ ， $\theta$ 也可表示為兩坐標點的夾角。

每隔 $30^\circ$ 標記一次的極坐標系， 2025 年 6 月 8 日擷取自維基百科。

極坐標的標記方法為 $(r, \theta)$ ，而角度 $\theta$ 也可以改為標示弧度。角度可以使用以下方式轉換為弧度：

$$ 角度 \times \frac{\pi}{180^\circ} = 弧度 $$

因此，可以有以下對應關係：

角度	$0^\circ$	$30^\circ$	$60^\circ$	$90^\circ$	$120^\circ$	$150^\circ$	$180^\circ$	$210^\circ$	$240^\circ$	$270^\circ$	$300^\circ$	$330^\circ$
弧度	$0$、$2 \pi$	$\frac{\pi}{6}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$\frac{2 \pi}{3}$	$\frac{5 \pi}{6}$	$\pi$	$\frac{7 \pi}{6}$	$\frac{4 \pi}{3}$	$\frac{3 \pi}{2}$	$\frac{5 \pi}{3}$	$\frac{11 \pi}{6}$

因為極坐標系與二維直角坐標系都處於二維平面中，因此極坐標也可以經由投影轉換為二維直角坐標。由上圖，我們可以知道極坐標與二維直角坐標的對應關係為

$$ \begin{align*} & x = r \cos \theta; \\ & y = r \sin \theta. \end{align*} $$

同樣地，我們也能夠從二維直角坐標轉換為極坐標

$$ \begin{align*} & r = \sqrt{x^2 + y^2}; \\ & \theta = \begin{cases} \arctan(\frac{y}{x}) & \text{if } x > 0; \\ \arctan(\frac{y}{x}) + \pi & \text{if } x < 0 \text{ and } y \ge 0; \\ \arctan(\frac{y}{x}) - \pi & \text{if } x < 0 \text{ and } y < 0; \\ \frac{\pi}{2} & \text{if } x = 0 \text{ and } y > 0; \\ -\frac{\pi}{2} & \text{if } x = 0 \text{ and } y < 0; \\ 0 & \text{if } x = 0 \text{ and } y = 0. \end{cases} \end{align*} $$

球坐標系

若無法查看互動式球坐標系，或是需要全螢幕檢視，請點此處前往。

球坐標系可視為是極坐標系的推廣，在極坐標系的基礎上多出一維度 $z$ ，使的球坐標系能解釋三維空間中的坐標。

球坐標的坐標標記方式為 $(\rho, \theta, \phi)$ ，其中

$x$ 軸、 $y$ 軸與 $z$ 軸是相互正交，且三軸相交處稱為原點，並標記為 $\textit{O}$ 。
$\rho$ 為坐標點與球心的距離。
$\theta$ 為 $xy$ 平面上由 $x$ 軸正方向朝 $y$ 軸正方向轉動的角度，且 $0 \leq \theta \leq 2 \pi$ 。
$\phi$ 為由 $z$ 軸正方向朝 $z$ 負方向轉動的角度，且 $0 \leq \phi \leq \pi$ 。

提醒

以上定義為數學界廣泛所接受的定義方式，物理學界所使用的定義方式與數學界存在些微差異，如下圖。

物理學界所使用的球坐標系，與數學界僅差異在對於角度的定義， 2025 年 6 月 8 日擷取自維基百科。

以下皆使用數學界定義之方式。

同樣地，球坐標系也能夠轉換為三維直角坐標系。從先前的互動式球坐標系，我們可以知道在 $xy$ 平面上

$$ \begin{align*} & x = r \cos \theta; \\ & y = r \sin \theta; \end{align*} $$

這是與極坐標系相同的。接下來，因為已知 $\overrightarrow{AB}$ 平行於 $z$ 軸，故由平行線的內錯角可知 $\overrightarrow{OA}$ 與 $z$ 軸的夾角會等同於 $\angle OAB$ 。由 $\triangle OAB$ ，我們可以知道

$$ r = \rho \sin \phi, $$

因此，就能得到球坐標與三維直角坐標的轉換為

$$ \begin{align*} & x = \rho \sin \phi \cos \theta; \\ & y = \rho \sin \phi \sin \theta; \\ & z = \rho \cos \phi. \end{align*} $$

而三維直角坐標與球坐標的轉換為

$$ \begin{align*} & \rho = \sqrt{x^2 + y^2 + z^2}; \\ & \theta = \arctan\left(\frac{y}{x}\right); \\ & \phi = \arctan\left(\frac{\sqrt{x^2 + y^2}}{z}\right). \end{align*} $$

參考資料

勒內·笛卡兒。（2025年3月4日）。維基百科，自由的百科全書。2025年6月9日參考自 https://zh.wikipedia.org/wiki/勒内·笛卡儿
笛卡兒坐標系。（2025年3月22日）。維基百科，自由的百科全書。2025年6月9日參考自 https://zh.wikipedia.org/zh-tw/笛卡儿坐标系
極坐標系。（2025年6月9日）。維基百科，自由的百科全書。2025年6月9日參考自 https://zh.wikipedia.org/wiki/极坐标系
弧度。（2025年3月15日）。維基百科，自由的百科全書。2025年6月9日參考自 https://zh.wikipedia.org/wiki/弧度
球座標系。（2025年2月8日）。維基百科，自由的百科全書。2025年6月9日參考自 https://zh.wikipedia.org/zh-tw/球座標系
黑筆紅筆。（2024年6月26日）。球座標轉換的公式 [影片]。YouTube。2025年6月9日參考自https://youtu.be/xxxqB-YnfX4