抽樣方法

封面圖片由 ChatGPT 生成。
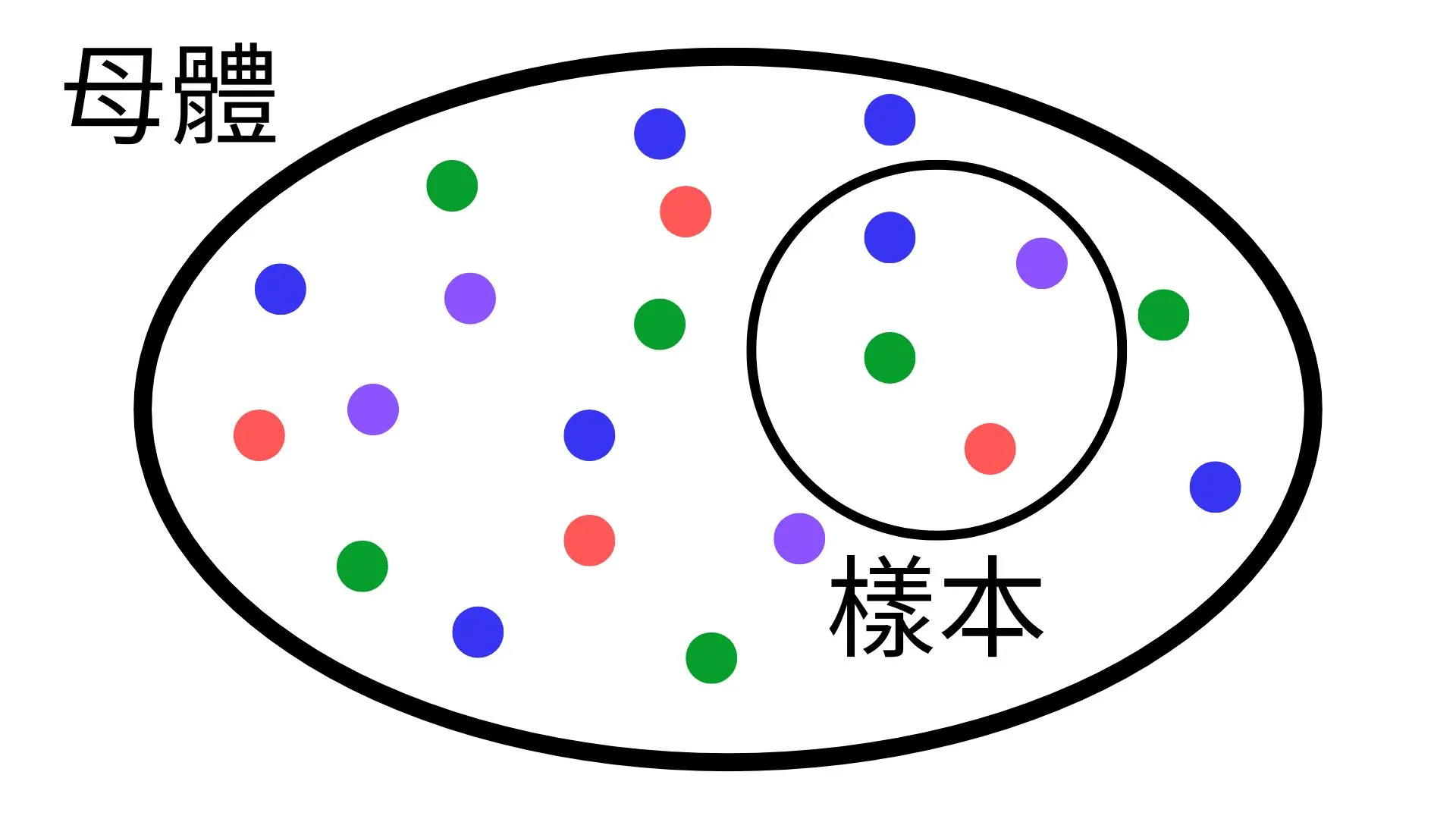
為什麼需要抽樣的方法呢?抽樣對資料分析有什麼好處?我們在建立模型時,有時候會發現需要訓練的資料量實在是太多,導致模型的訓練時間被拉長。而抽樣的目的在於,從龐大的母群體(population ,母體)中選取具有代表性的有限樣本(sample),並依據選取的樣本進行統計,從而反推樣本所在的母群體的性質或特性。
從以上敘述,我們可以知道樣本是母體的子集合。而如何從母體中找出合理的子集合作為樣本,就是抽樣方法(sampling method)。由於抽樣的樣本與母體仍會存在數量上的差異,我們希望經由抽樣選擇的樣本所計算出的樣本統計量(sample statistic),能夠靠近母體統計量(population statistic),並儘量降低因抽樣所造成的偏誤(bias)。
樣本品質
樣本品質會受到以下因素的影響:
- 樣本數量
- 抽樣方法
樣本數量過少,可能會造成代表性不足,無法反映母體性質;而選擇不合適的抽樣方法,則有可能未選取到重要資料點,遺漏母體特徵。
依據中央極限定理(central limit theorem, CLT),當樣本數量足夠大時,樣本平均數 $\overline{X}$ 會近似常態分佈(normal distribution)即
$$ \overline{X} \sim N(\mu, \sigma^2) $$
其中, $\mu$ 是母體平均數; $\sigma^2$ 是母體變異數。通常樣本數量 $n$ 多於 30 時,其樣本平均數集會近似常態分佈,而其樣本變異數為
$$ \sigma^2_{\overline{X}} = \frac{\sigma^2}{n} $$
簡單隨機抽樣
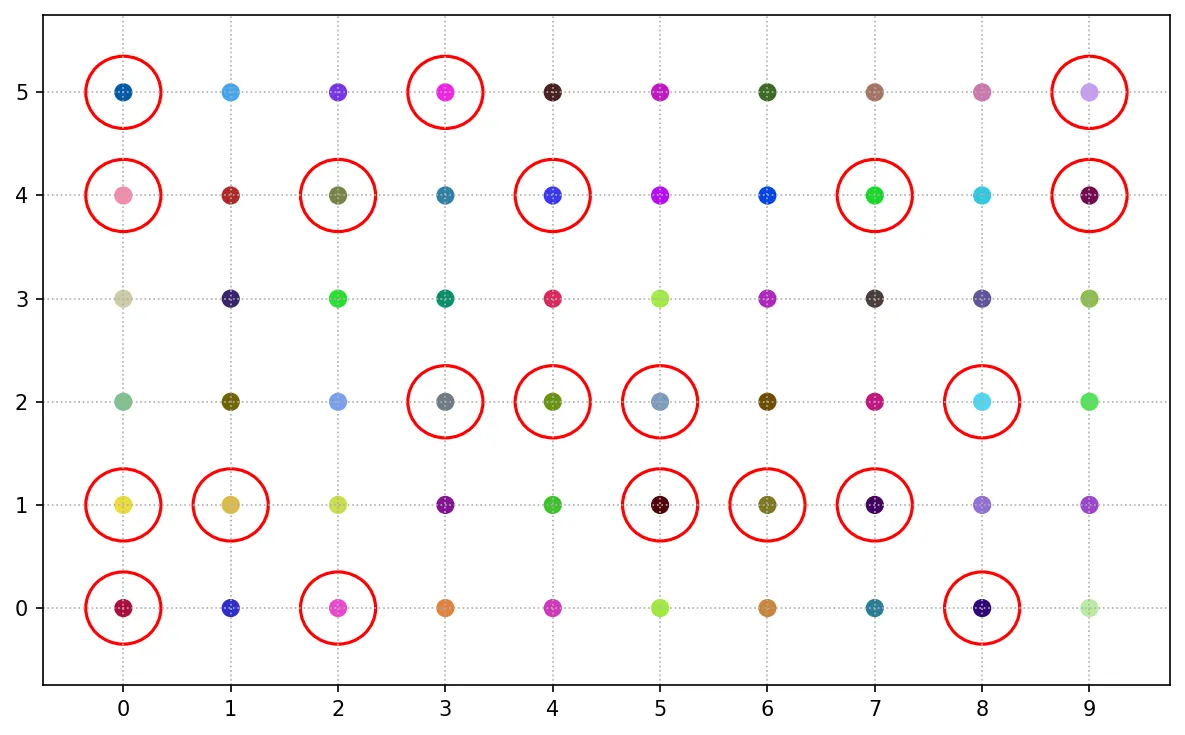
簡單隨機抽樣是最常見的抽樣方法,其抽樣原理為每個個體均有相等機會被選取為樣本。
簡單隨機抽樣的抽樣過程獨立,且每次抽樣互不影響。
系統抽樣
系統抽樣是以等距的方式從母體中選取樣本,其抽樣原理為以隨機個體開始,以相同間距選取樣本。
一階段叢集抽樣
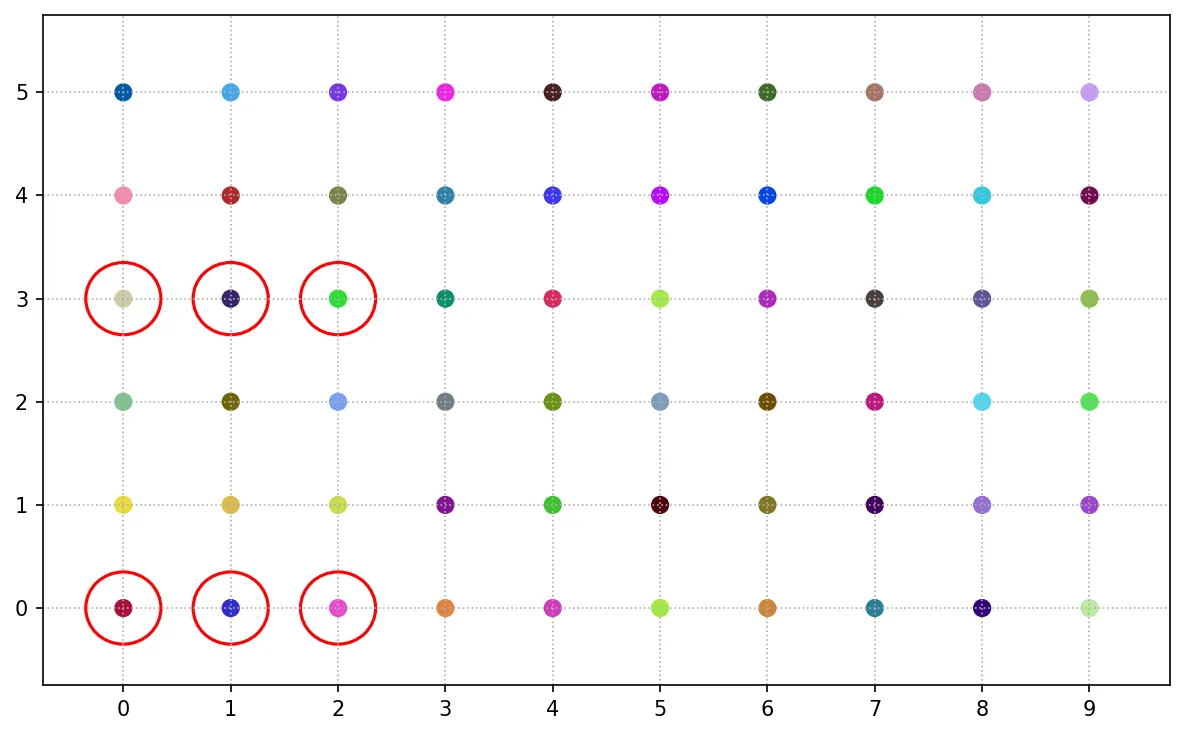
一階段叢集抽樣得先事前分組,其抽樣原理是將母體分為多個叢集,且各叢集間同質,叢集內異質。並隨機選取從集,以叢集內的所有個體作為樣本。
以下每行作為一個叢集,共 6 個。
二階段叢集抽樣
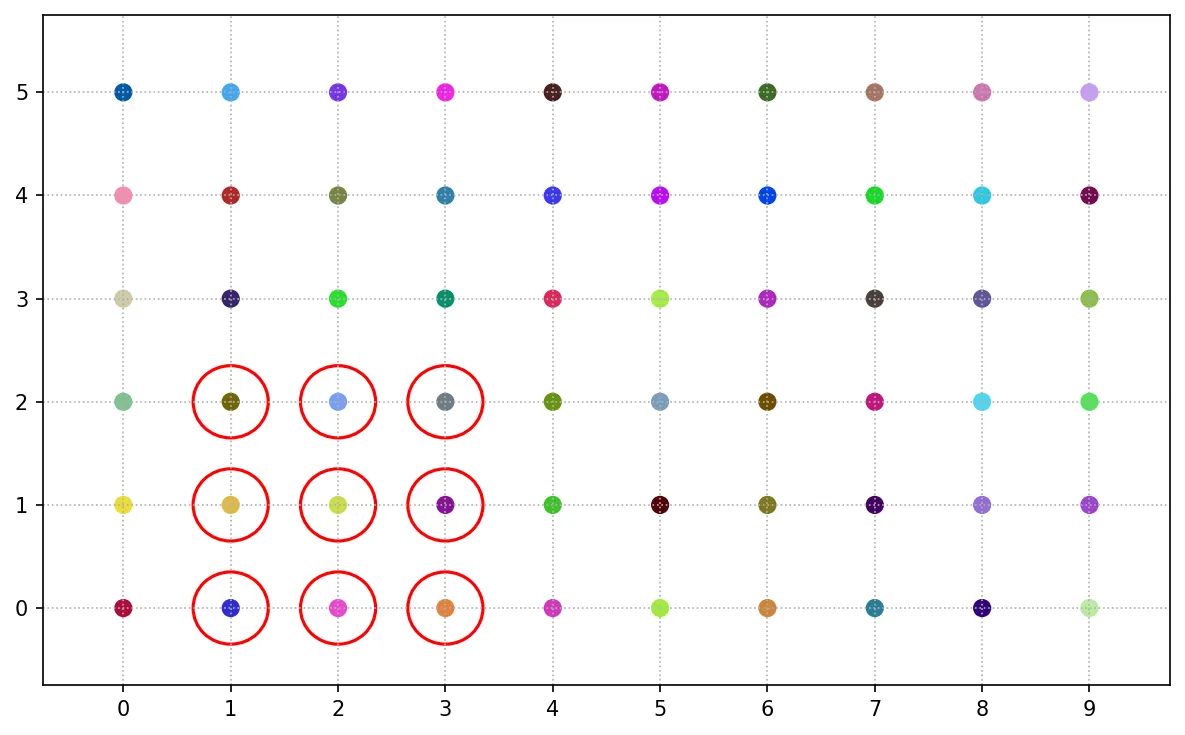
二階段叢集抽樣與一階段叢集抽樣類似,不過我們會在進行二階段叢集抽樣時,於被選中的叢集內再額外進行簡單隨機抽樣。
叢集抽樣不一定只會選取一個叢集,有時會重複選取多個叢集做為樣本組。
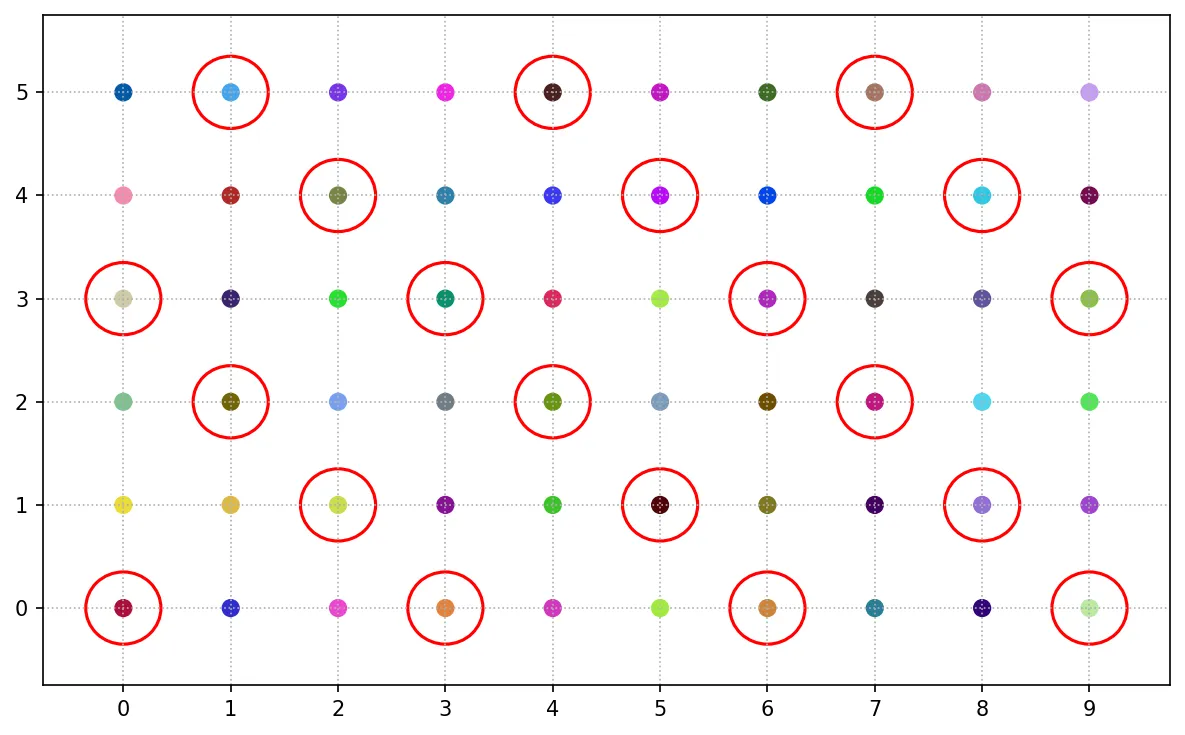
分層隨機抽樣
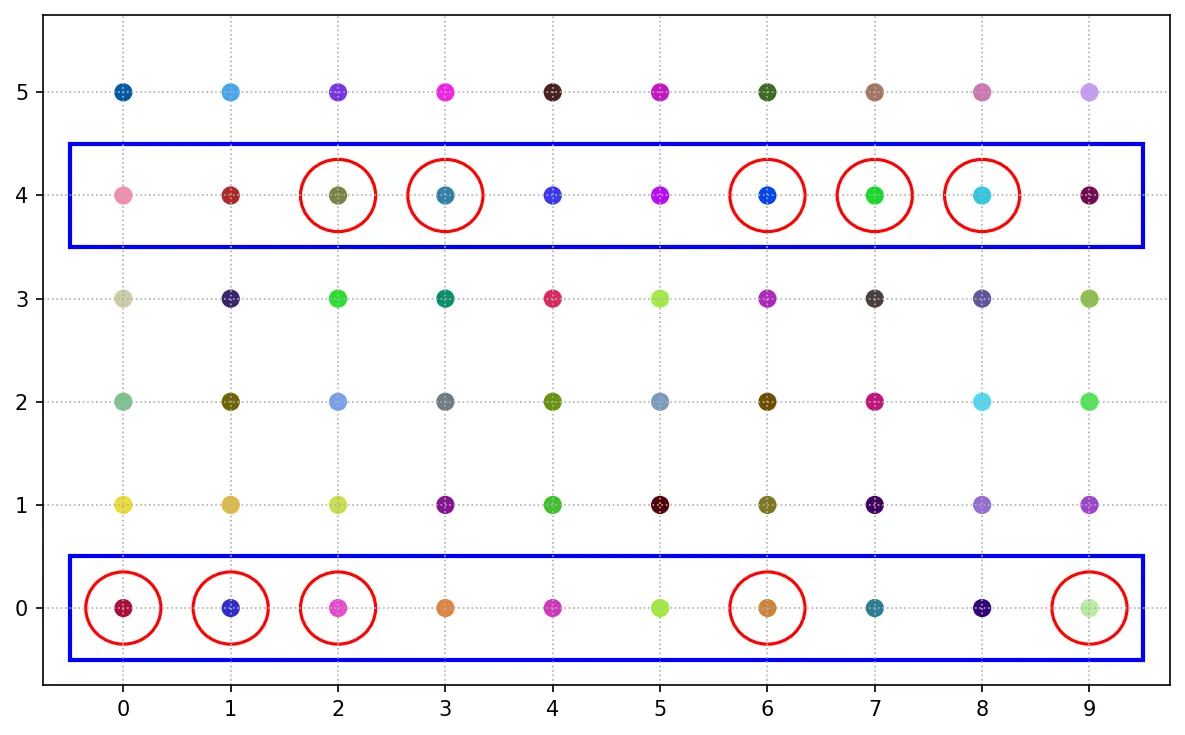
進行分層隨機抽樣時,母體會被分為多個異質性的子集,再從各子集依比例或數量進行簡單隨機抽樣。多用於比較不同組別的研究,如單親家庭組、完整家庭組。
以下依行分為 6 組,編號為 0 至 5 ,每行抽選 2 個個體作為樣本。
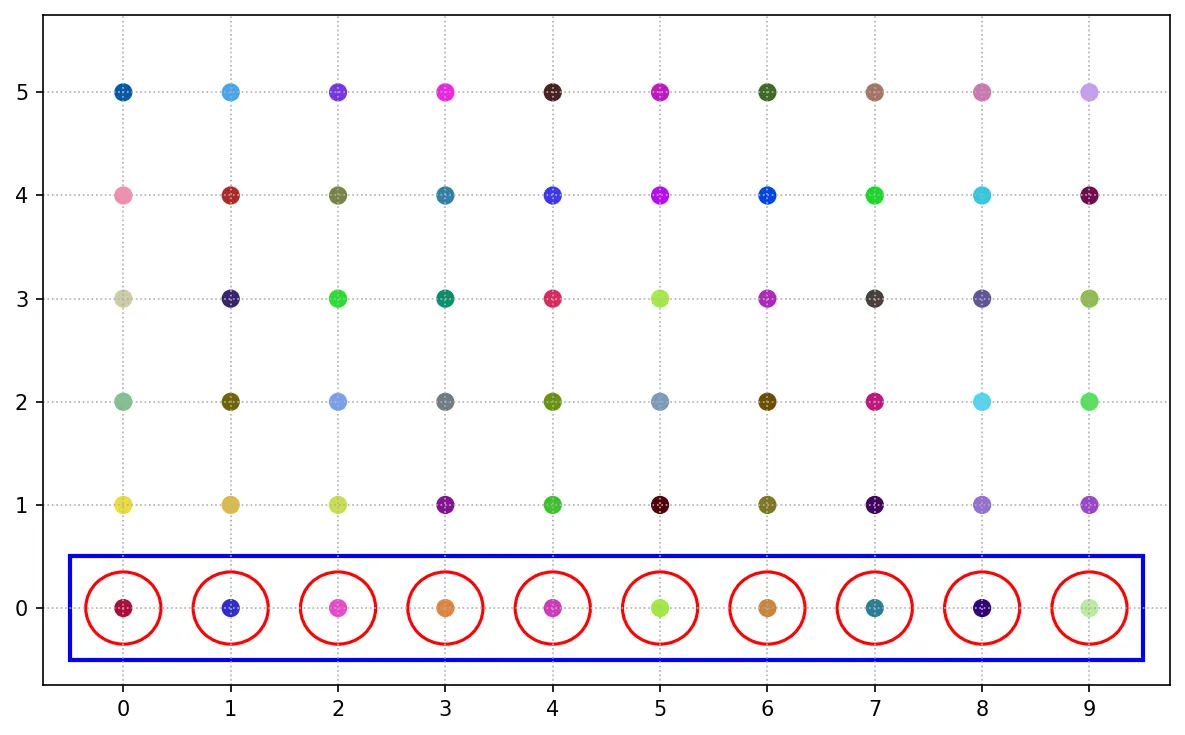
便利抽樣
便利抽樣只為研究方便,只選擇對於研究最方便、快速的個體作為樣本。其樣本選擇與母體的誤差可能會很大。
常用的情境可能是:為求簡便,在問卷填答時只選取前 9 個完成度最高的做為研究樣本。
判斷抽樣
判斷抽樣是根據研究者的專業判斷或經驗選取樣本的方法,其選取樣本方式具有主觀意圖。
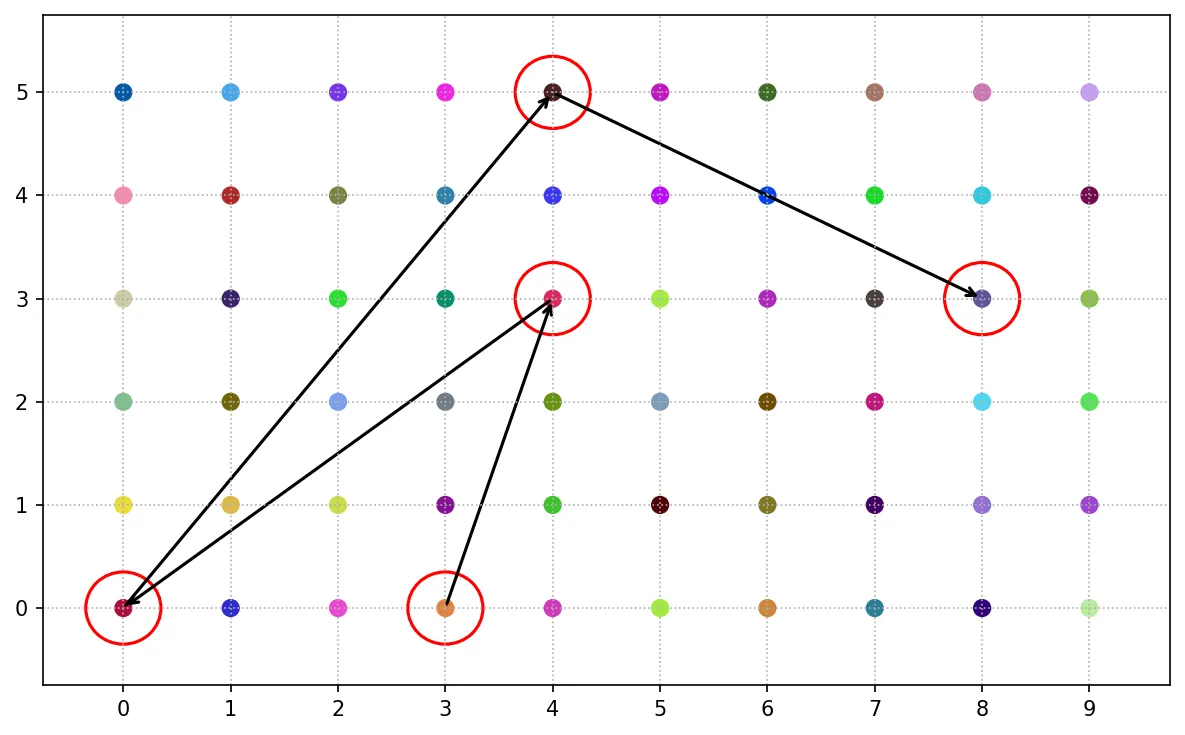
參照抽樣
參照抽樣又稱為雪球抽樣,其抽樣方法為先選取某一個體,再選取與該個體有關的其他個體作為樣本,以此類推。
參照抽樣常用於社群或網路分析、族群或特殊行業調查等。
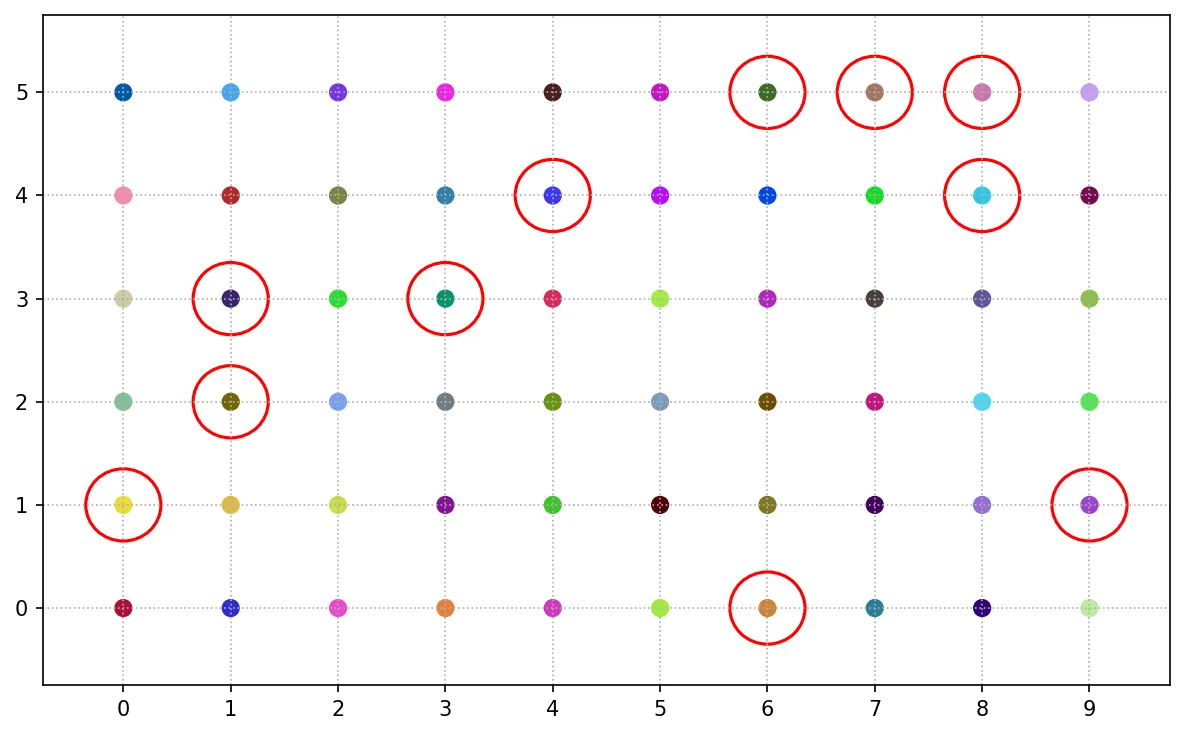
定額抽樣
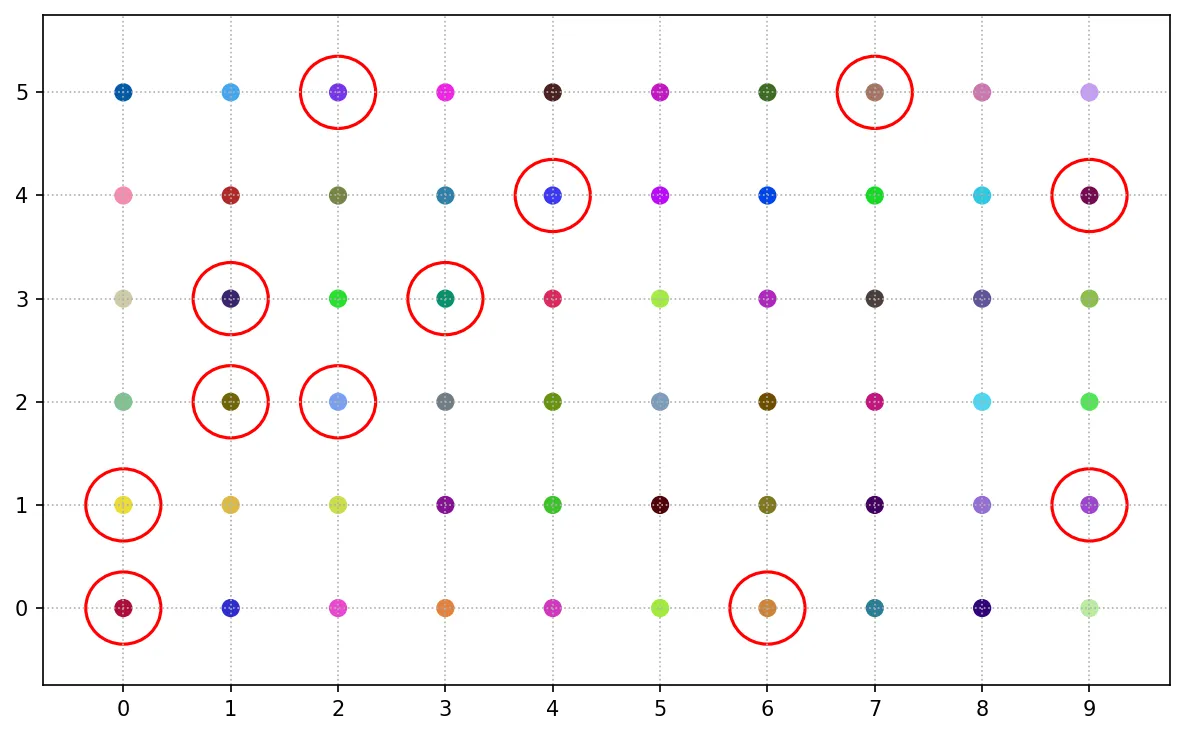
定額抽樣與分層隨機抽樣類似,母體會被分為多個異質性的子集,再從各子集依判斷取樣或便利取樣選取固定數量以內的樣本,主要選取具代表性或便利的個體作為樣本。
以下依行分為 6 組,編號為 0 至 5 ,每行依判斷取樣選取 4 個以內的樣本。
結語
抽樣方法是研究者進行研究、建模與資料分析的基本知識。在母體規模不大的情況下,通常會直接使用整個母體進行分析;但當母體過大時,抽樣就變得非常重要。抽樣也常用於將資料分為多個訓練集與測試集,以進行不同的驗證與測試。
在上述各種抽樣方法中,我們可以將它們分為兩大類:機率抽樣(Probability Sampling)與非機率抽樣(Non-Probability Sampling),如下:
機率抽樣
每個個體被抽中的機會可量化且非零。
- 簡單隨機抽樣
- 系統抽樣
- 分層抽樣
- 叢集抽樣
非機率抽樣
個體被抽中的機會不易量化,依賴研究者判斷或方便性。
- 便利抽樣
- 判斷抽樣
- 參照抽樣
- 定額抽樣
選擇合適的抽樣方法,能夠提高樣本代表性、降低偏差,並讓研究結果更可靠。
延伸學習
- 本文使用的 ipynb 檔案。
參考資料
吳明隆(2010)。抽樣方法。論文寫作與量化研究(二版,頁 78-88)。臺北市:五南圖書出版股份有限公司。
母體 (統計學)。(2025年7月14日)。維基百科,自由的百科全書。2025年7月15日參考自 https://zh.wikipedia.org/wiki/总体